Алгоритм Форда

Основные понятия теории сетевых моделей

Сетевое планирование

Изучаемые вопросы:

1. Основные понятия теории сетевых моделей

2. Алгоритм Форда

Методы сетевого планирования разработаны в 60-е гг. двадцатого столетия. Методы сетевого планирования относятся к одному из разделов современной теории управления большими системами и предназначены для составления и наблюдения за исполнением проектов производства или исследований. Впервые сетевые методы планирования были оформлены в США в виде системы ПЕРТ или метода критического пути («Critical Path Scheduling»). Математической основой этих методов служит теория графов, которая является, в свою очередь, частью теории множеств.

Рассмотрим множество, состоящее из конечного числа элементов, которые мы будем обозначать буквами x₁, x₂,..., х_n, а само множество буквой X. Запишем это символически: X = { x₁, x₂,..., х_n}.

Каждому элементу х_i, принадлежащему X, поставим в соответствие нуль, один или несколько элементов из X. Тогда мы построим, пользуясь терминологией теории множеств, некоторый «граф». Обозначим через Г закон, предоставляющий данное соответствие, и запишем граф символически G = (X, Г).

Граф может быть представлен с помощью чертежа, это называется представление графа с помощью направленных дуг, или с помощью таблицы с двумя входами (матрица).

Для примера рассмотрим множество из 5 элементов: Х= {А, В, С, D, Е). Пусть закон Г, определяющий соответствие между элементами этого множества, определен следующим образом: ГА = {В, С, D}, ГВ = {В}, ГС = {D, E}, ГD = {А, С}, ГЕ = О, где символ О означает пустое множество. На рис. 7 представлено графическое изображение этого графа, а в таблице рис. 8 — его табличное задание.

	A	B	C	D	E
A
B
C
D
E

На данном примере удобно проиллюстрировать все основные понятия, которые используются в теории графов.

Вершиной графа называется элемент множества, образующего граф. На рис. 7 вершины графа, которые часто также называют точками, это элементы множества А, В, С, D, Е. Дугой графа называется ориентированная пара вершин графа. На рис 7. дугами являются пары: (А, В), (А, С), (С, D) и т. д.

Путем называется последовательность сцепленных дуг, позволяющих пройти из одной вершины в другую. На рис. 7 пути: (А, С, Е), (А, С, D),(D, С, В) и т. п.

Контуром называется путь, начальная вершина которого совпадает с конечной. На рис. 1 контуром является путь (А, С, D, А).

Петлей называется дуга, начало и конец которой совпадают (В, В).

Ребром называется неориентированная дуга, т. е. дуга, у которой не указано направление движения.

Цепью называется сцепленная последовательность ребер.

Граф называется связным, если между всякой парой его вершин существует хотя бы одна цепь.

Предком некоторой вершины называется вершина, из которой исходит дуга, входящая в данную вершину.

Потомком некоторой вершины называется вершина, в которую входит дуга, исходящая из данной вершины.

В дальнейшем будем рассматривать связные графы без контуров.

Для связного графа без контуров возникает и решается задача разбиения его вершин на слои так, чтобы:

а) все элементы данного слоя не имели предков в следующем слое, а элементы последнего – потомков;

б) порядок вершин внутри одного и того же слоя безразличен, т. е. эти вершины не соединены между собой дугами.

Для решения этой задачи используются различные методы. Один из них состоит в том, что на чертеже графа последовательно вычеркивают (фиксируют) вершины, не имеющие предков, которые и составляют соответствующий слой.

Самый длинный путь в сетевом графике определит кратчайшие сроки выполнения всего проекта, если работы будут выполняться без сбоев. Этот путь называется критическим, а работы, его составляющие, и события, лежащие на нем, называются критическими. Таким образом, критический путь представляет те операции (работы), на ход выполнения которых руководитель проекта должен обратить все свое внимание, так как от их своевременного выполнения зависит общий срок выполнения проекта.

Критическим путем сетевого графика называется самый длинный путь.

Работы и события, не лежащие на критическом пути, в связи с тем, что они лежат на более коротких путях сетевого графика, могут выполняться с некоторым опозданием (резервы времени) без угрозы срыва общего срока выполнения проекта.

Для расчета времени выполнения проекта и соответственно определения критического пути необходимо, двигаясь сверху вниз по графику, рассчитать ранний срок наступления событий.

Ранний срок наступления события определяется по формулам:

t₁ = 0,

,

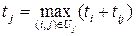где:

t₁ – время начала выполнения проекта;

t_j – ранний срок наступления j-го события; продолжительность выполнения операции (i, j), идущей из вершины i в вершину j;

U_j – подмножество дуг, входящих в вершину j.

Предельный срок наступления события определяется по формулам:

t₁ = 0,

,

где:

t₁ – время начала выполнения проекта;

t_n – срок завершения проекта;

t_j^* – поздний (предельный) срок наступления j- гoсобытия;

t_ij – продолжительность выполнения операции (i, j), идущей из вершины i в вершину j

U_j^*– подмножество дуг, исходящих из вершины

Предельный срок наступления событий рассчитывается при движении по сетевому графику в обратном направлении – от конца к началу.

Резервы событий и операций определяются следующими соотношениями.

Резерв времени i-го события:

Полный резерв времени операции:

Свободный резерв времени операции:

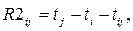
Независимый резерв времени операции:

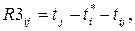
Для нахождения критического пути и срока завершения проекта разработан ряд алгоритмов. Приведем один из них.

1. Отметить каждую вершину индексом . Положить все .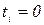

2. Найти такую дугу , что 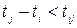, и заменить на . Заметим, что 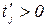, если .

3. Продолжать так до тех пор, пока не останется дуг, приводящих к увеличению .

Существует вершина такая, что , так как монотонно возрастает в течении процедуры 2) – 3) и вершина является последней вершиной, использованной для увеличения .

Точно также пусть вершина такова, что , и т.д.

Так как последовательность , , 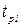, … является строго убывающей, то в некоторый момент времени получим, что .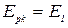

Тогда будет величиной самого длинного пути из в (продолжительность реализации проекта) и последовательность вершин , определит критический путь.

Контрольные вопросы:

1. Сетевая модель, ее характеристика и особенности.

2. Области применения и эффективность сетевых моделей.

3. В чем состоит технология построения сетевых графиков (ра­боты, события, критический путь)?

4. Каковы правила построения сетевого графика?

5. Как рассчитать временные параметры сетевого графика, продолжительность критического пути?

6. Что понимается под полным и частным резервами времени?

7. Как отразить расчет параметров сетевой модели на графике и в таблице?

8. Как оптимизировать сетевую модель по критерию времени?

Дата добавления: 2013-12-13