Решение. Областью определения функции является все множество действительных чисел, за исключением нуля, то есть

Областью определения функции является все множество действительных чисел, за исключением нуля, то есть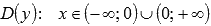. Оба отрезка попадают в область определения.

Находим производную функции по правилу дифференцирования дроби:

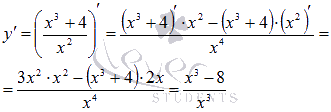
Стационарные точки определим из уравнения 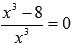. Единственным действительным корнем является x = 2. Эта стационарная точка попадает в первый отрезок [1; 4].

• Для первого случая вычисляем значения функции на концах отрезка и в стационарной точке, то есть при x = 1, x = 2 и x = 4:
  
  
  
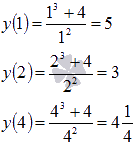
  Следовательно, наибольшее значение функции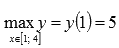 достигается при x = 1, а наименьшее значение 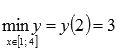– при x = 2.

• Для второго случая вычисляем значения функции лишь на концах отрезка [-4; -1] (так как он не содержит ни одной стационарной точки):
  
  
  
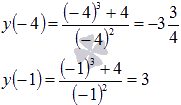
  Следовательно, .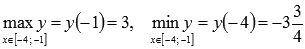

Алгоритм нахождения наибольшего и наименьшего значения непрерывной функции на открытом или бесконечном интервале X.

Рекомендуем повторить определения одностороннего предела и предела на бесконечности, а также способы нахождения пределов.

1. Проверяем, является ли интервал X подмножеством области определения функции.

2. Определяем все стационарные точки, попадающие в промежуток X. Для этого приравниваем производную функции к нулю, решаем полученное уравнение и выбираем подходящие корни.
Если стационарных точек нет или ни одна из них не попадает в интервал, то переходим к следующему пункту.

3. Вычисляем значения функции в отобранных стационарных точках.
Дальнейшие действия зависят от интервала X.
Если интервал X имеет вид:

o [a; b), то вычисляем значение функции в точке x = a и односторонний предел ;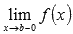

o (a; b], то вычисляем значение функции в точке x = b и односторонний предел ;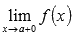

o (a; b), то вычисляем односторонние пределы ;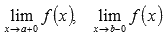

o 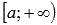, то вычисляем значение функции в точке x = a и предел на плюс бесконечности ;

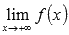o 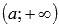, то вычисляем односторонний предел 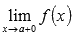и предел на плюс бесконечности ;

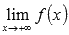o 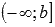, то вычисляем значение функции в точке x = b и предел на минус бесконечности ;

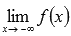o 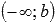, то вычисляем односторонний предел 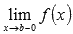и предел на минус бесконечности ;

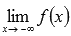o 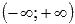, то вычисляем пределы на плюс и минус бесконечности .

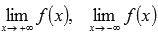Пример. Найти наибольшее и наименьшее значение функции 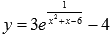на интервалах:

• 

Решение. Начнем с области определения функции. Квадратный трехчлен в знаменателе дроби не должен обращаться в ноль:

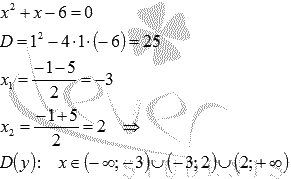
Легко проверить, что все интервалы из условия задачи принадлежат области определения функции.

Найдем стационарные точки. Для этого сначала продифференцируем функцию:

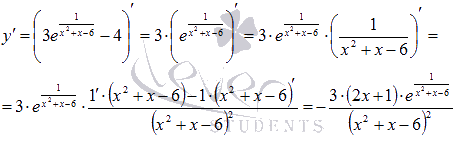
Производная обращается в ноль при 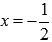. Эта стационарная точка попадает в интервалы (-3; 1] и (-3; 2).

• Для первого промежутка 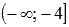вычисляем значение функции при x = -4 и предел на минус бесконечности:
  
  
  
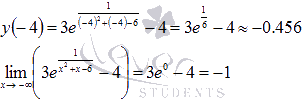
  Так как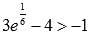 , то 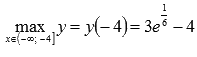, а о наименьшем значении функции выводов сделать нельзя. Можно лишь утверждать, что значения функции ограничены снизу значением -1 (на минус бесконечности значения функции асимптотически приближаются к прямой y = -1).

Дата добавления: 2014-01-04