Лекция 14. § 166. Определение поверхности второго порядка по отношению к ДПСК

Аналитическая геометрия.

Глава 12. Поверхности второго порядка, заданные общими уравнениями

Для того, чтобы определить расположение поверхности второго порядка, заданной общим уравнением (1) относительно ДПСК:

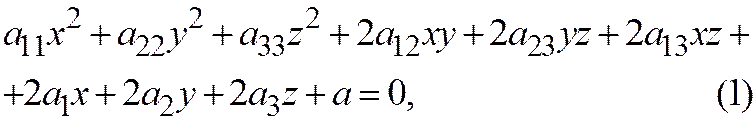
надо знать каноническое уравнение поверхности второго порядка и знать ту систему координат, в которой уравнение поверхности будет иметь канонический вид, а для этого необходимо знать новое начало координат этой системы и направление её осей.

Для центральных поверхностей достаточно найти координаты центра из системы уравнений:

(2)

и координаты векторов, имеющих главные направления. Координаты этих векторов находятся из системы:

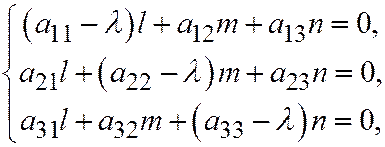(3)

где вместо надо подставлять корни характеристического уравнения. Характеристическое уравнение имеет вид: .

В случае центральных поверхностей вращения достаточно найти координаты центра и координаты направляющего вектора оси вращения, соответствующего простому корню характеристического уравнения (что такое простой корень, мы знаем). В случае сферы достаточно определить координаты её центра и её радиус.

В случае, если общее уравнение поверхности второго порядка является уравнением эллиптического или гиперболического цилиндра, вопрос о расположении решается так: уравнения (2) являются уравнениями места центров (прямая линия); координаты векторов главных направлений (если данная поверхность не является круговым цилиндром) находятся из системы (3), куда надо подставлять вместо отличные от нуля корни характеристического уравнения.

Если рассматриваемое уравнение является уравнением прямого кругового цилиндра, то для определения его расположения достаточно знать уравнения его оси (система (2)) и радиус.

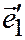Для параболоидов надо определить координаты вершины , координаты векторов , , имеющих главные направления, координаты вектора 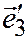, к ним перпендикулярного, и каноническое уравнение в сис-теме 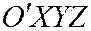, в которой за положительное направление осей 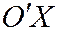, , 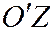взяты соответственно направления векторов 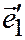, , и 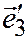. Для параболоида вращения достаточно определить координаты вершины и координаты вектора, коллинеарного оси вращения.

В отличие от центральных поверхностей при определении вектора 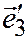для параболоидов нужно знать не только прямую, направление которой этот вектор определяет, но и направление того луча, который направлен внутрь параболы.

Так вот, вектор 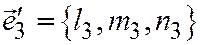, координаты которого определяются из системы (3) при :

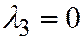(4)

будет направлен внутрь сечения параболоида, если:

.

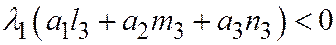Вершина параболоида находится так. Возьмём на поверхности параболоида точку 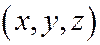. Координаты вектора, нормального к касательной плоскости в этой точке поверхности, таковы:

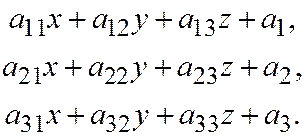(5)

И, значит, точка 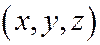будет вершиной поверхности тогда и только тогда, когда эти координаты пропорциональны координатам вектора, коллинеарного направлению 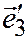, то есть:

(6)

Умножая эти равенства соответственно на 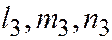и складывая почленно, в силу соотношений (4) то есть:

получим:

.

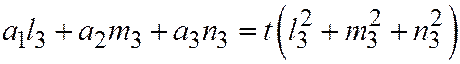Отсюда находим: .

Переписывая уравнение поверхности в виде:

в силу соотношений (6), получим:

(7)

Таким образом, для нахождения координат вершины надо решить линейную систему (6), (7):

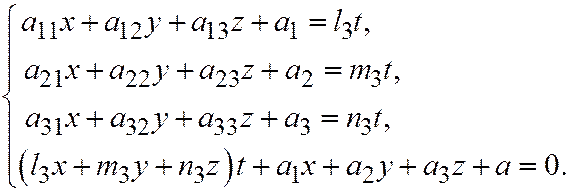(8)

Предварительно определив параметр из уравнения:

.

Если уравнение поверхности второго порядка является уравнением параболического цилиндра, то уравнение (1) можно записать в виде:

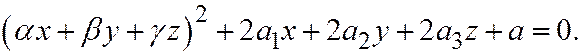
Отсюда видно, что поверхность образована пересечением двух плоскосте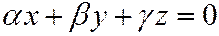й:

и .

Эти плоскости пересекаются по прямой линии, кото-рая является образующей параболического цилиндра. Вектор 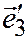- направляется вдоль этой линии.

Координаты вектора 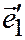, направленного перпендикулярно оси параболы (это уже в плоскости, перпендикулярной образующей) находятся из системы уравнений (3), где вместо надо положить :

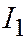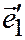Вектор , направленный вдоль оси параболы на-ходится как векторное произведение векторов и 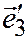: 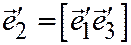. Теперь, если 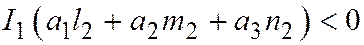, то вектор направлен внутрь параболы и наружу в противном случае.

Дата добавления: 2014-01-04