
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Закони розподілу та основні характеристики випадкових процесів
|
|
|
|
Відомо, що ймовірнісні властивості випадкової величини можна вивчати за допомогою її функції розподілу  : ймовірність того, що випадкова величина
: ймовірність того, що випадкова величина 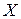 прийме значення, яке є меншим від заданого числа
прийме значення, яке є меншим від заданого числа  . Нагадаємо також, що для дискретної випадкової величини її закон розподілу може бути заданий рядом розподілу, для неперервної випадкової величини – густиною розподілу. Аналогічно ймовірнісні властивості випадкового процесу можна вивчити за допомогою сім’ї його скінченно-вимірних розподілів. Останні отримуються так само, як і розподіл скінченної множини випадкових величин, визначених на одному і тому ж імовірнісному просторі.
. Нагадаємо також, що для дискретної випадкової величини її закон розподілу може бути заданий рядом розподілу, для неперервної випадкової величини – густиною розподілу. Аналогічно ймовірнісні властивості випадкового процесу можна вивчити за допомогою сім’ї його скінченно-вимірних розподілів. Останні отримуються так само, як і розподіл скінченної множини випадкових величин, визначених на одному і тому ж імовірнісному просторі.
Нехай маємо випадковий процес  . У кожному перерізі розподіл ймовірностей випадкового процесу задається одновимірною функцією розподілу:
. У кожному перерізі розподіл ймовірностей випадкового процесу задається одновимірною функцією розподілу:
 . (3)
. (3)
Якщо випадкова величина  дискретна, то одновимірний закон розподілу випадкового процесу
дискретна, то одновимірний закон розподілу випадкового процесу  описується рядом розподілу
описується рядом розподілу
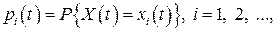 (4)
(4)
де  – значення випадкової величини
– значення випадкової величини  . Якщо випадкова величина
. Якщо випадкова величина  неперервна, то цей закон можна задати за допомогою одновимірної густини розподілу
неперервна, то цей закон можна задати за допомогою одновимірної густини розподілу  , для якої при будь-яких
, для якої при будь-яких 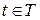 та
та 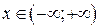 виконується рівність
виконується рівність

Очевидно, в точках неперервності  маємо
маємо
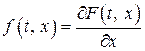 .
.
Неважко зрозуміти, що функція 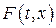 не дає повної, вичерпної імовірнісної характеристики випадкового процесу, оскільки вона не враховує залежності випадкових величин
не дає повної, вичерпної імовірнісної характеристики випадкового процесу, оскільки вона не враховує залежності випадкових величин  при різних
при різних 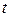 (тобто залежності різних перерізів випадкового процесу). Більш повно ймовірнісні властивості
(тобто залежності різних перерізів випадкового процесу). Більш повно ймовірнісні властивості  описує
описує  -вимірна функція розподілу – функція розподілу випадкового вектора
-вимірна функція розподілу – функція розподілу випадкового вектора 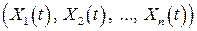 для
для  перерізів випадкового процесу:
перерізів випадкового процесу:
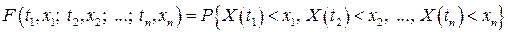 .
.
Однак практичне застосування знаходять лише функція 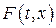 та функція розподілу другого порядку
та функція розподілу другого порядку
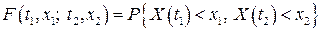 (5)
(5)
Очевидно, скінченновимірні розподіли випадкового процесу підпорядковуються певним правилам узгодження. Наприклад, якщо  , то ці умови виглядають так:
, то ці умови виглядають так:
|
|
|
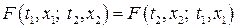 , (6)
, (6)
 , (7)
, (7)
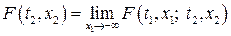 , (8)
, (8)
Якщо випадкова величина  неперервна і
неперервна і 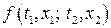 – густина розподілу функції розподілу
– густина розподілу функції розподілу  , то
, то
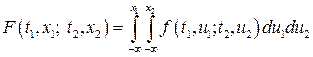 , (9)
, (9)
 . (10)
. (10)
Звідси, зокрема, випливають формули
 , (11)
, (11)
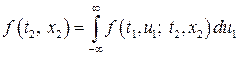 , (12)
, (12)
які можна розглядати як еквіваленти умов узгодження (7), (8).
До важливих характеристик випадкового процесу належать поняття його математичного сподівання, дисперсії, а також кореляційної функції або коваріації, які є природними узагальненнями аналогічних понять, що були введені для випадкових величин.
Означення. Математичним сподіванням випадкового процесу  називається невипадкова функція
називається невипадкова функція  , яка для кожного фіксованого значення
, яка для кожного фіксованого значення 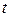 визначається як математичне сподівання відповідного перерізу випадкового процесу, тобто
визначається як математичне сподівання відповідного перерізу випадкового процесу, тобто
 . (13)
. (13)
З даного означення випливає, що у випадку, коли переріз випадкового процесу  при заданому
при заданому 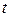 є дискретною випадковою величиною з рядом розподілу
є дискретною випадковою величиною з рядом розподілу

| 
| 
| 
| 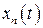
|

| 
| 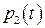
| 
| 
|
то його математичне сподівання можна обчислити за формулою
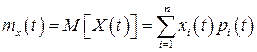 . (15)
. (15)
Якщо переріз випадкового процесу  при заданому
при заданому 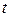 є неперервною випадковою величиною з густиною розподілу
є неперервною випадковою величиною з густиною розподілу  , то його математичне сподівання може бути обчислене за формулою
, то його математичне сподівання може бути обчислене за формулою
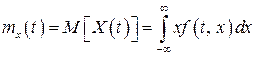 . (16)
. (16)
Функція  представляє деяку невипадкову «середню функцію», навколо якої групуються реалізації випадкового процесу.
представляє деяку невипадкову «середню функцію», навколо якої групуються реалізації випадкового процесу.
Означення. Дисперсією випадкового процесу  називається невипадкова функція
називається невипадкова функція  , яка для кожного фіксованого значення
, яка для кожного фіксованого значення 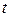 визначається як дисперсія відповідного перерізу випадкового процесу, тобто
визначається як дисперсія відповідного перерізу випадкового процесу, тобто
 (17)
(17)
або
 . (18)
. (18)
У випадку, коли переріз випадкового процесу  при заданому
при заданому 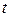 є дискретною випадковою величиною з рядом розподілу (14), то його дисперсія обчислюється за формулою
є дискретною випадковою величиною з рядом розподілу (14), то його дисперсія обчислюється за формулою
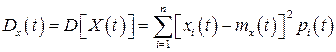 (19)
(19)
або
 . (20)
. (20)
Якщо переріз випадкового процесу  при заданному
при заданному 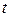 є неперервною випадковою величиною з густиною розподілу
є неперервною випадковою величиною з густиною розподілу  , то його дисперсія обчислюється за формулою:
, то його дисперсія обчислюється за формулою:
|
|
|
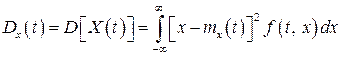 (21)
(21)
або
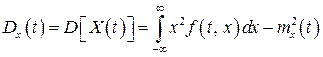 . (22)
. (22)
Функція 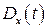 представляє невипадкову невід’ємну функцію, яка характеризує ступінь розсіювання реалізацій випадкового процесу навколо його математичного сподівання.
представляє невипадкову невід’ємну функцію, яка характеризує ступінь розсіювання реалізацій випадкового процесу навколо його математичного сподівання.
Означення. Середнім квадратичним відхиленням  випадкового процесу називається арифметичне значення кореня квадратного з дисперсії
випадкового процесу називається арифметичне значення кореня квадратного з дисперсії 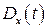 :
:
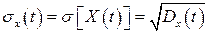 . (23)
. (23)
Розмірність функції  збігається з розмірністю випадкового процесу
збігається з розмірністю випадкового процесу  .
.
Слід відзначити, що введені нами характеристики випадкового процесу  , а саме: математичне сподівання
, а саме: математичне сподівання  , дисперсія
, дисперсія 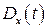 та середнє квадратичне відхилення
та середнє квадратичне відхилення  визначаються тільки одновимірним законом розподілу. Якщо відома двовимірна функція розподілу випадкового процесу, то завжди для будь-яких двох перерізів випадкового процесу можна знайти їх коваріацію, яку в цьому випадку частіше називають кореляційною функцією.
визначаються тільки одновимірним законом розподілу. Якщо відома двовимірна функція розподілу випадкового процесу, то завжди для будь-яких двох перерізів випадкового процесу можна знайти їх коваріацію, яку в цьому випадку частіше називають кореляційною функцією.
Означення. Кореляційною функцією випадкового процесу  називається невипадкова функція
називається невипадкова функція 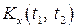 двох аргументів
двох аргументів  і
і 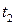 , яка при будь-яких значеннях
, яка при будь-яких значеннях  і
і 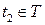 дорівнює кореляційному моменту відповідних перерізів випадкового процесу:
дорівнює кореляційному моменту відповідних перерізів випадкового процесу:
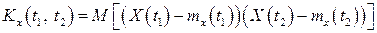 (24)
(24)
або
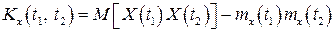 . (25)
. (25)
Якщо, наприклад, для двох перерізів  і
і 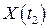 випадкового процесу
випадкового процесу  відома їх сумісна густина розподілу
відома їх сумісна густина розподілу 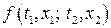 , то формули (24), (25) набудуть вигляду:
, то формули (24), (25) набудуть вигляду:
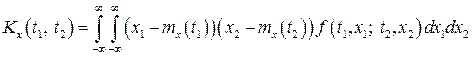 (26)
(26)
або
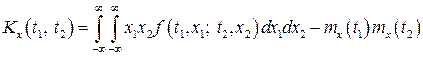 . (27)
. (27)
Кореляційна функція характеризує залежність між випадковими величинами  і
і 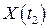 – перерізами випадкового процесу
– перерізами випадкового процесу  при
при  і
і  . Чим слабший зв’язок між випадковими величинами
. Чим слабший зв’язок між випадковими величинами  і
і 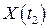 , тим менше значення кореляційної функції
, тим менше значення кореляційної функції 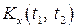 . Але чим слабший цей зв’язок, тим швидше змінюються значення, які приймає випадковий процес.
. Але чим слабший цей зв’язок, тим швидше змінюються значення, які приймає випадковий процес.
Теорія, яка вивчає випадкові процеси на підставі аналізу перших двох моментів випадкового процесу, до яких належать математичне сподівання, дисперсія та кореляційна функція називається кореляційною теорією.
Відзначимо основні властивості кореляційної функції 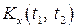 випадкового процесу
випадкового процесу  .
.
1. За умови рівності аргументів  кореляційна функція випадкового процесу дорівнює його дисперсії. Справді,
кореляційна функція випадкового процесу дорівнює його дисперсії. Справді,
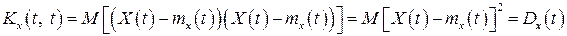 .
.
2. Кореляційна функція 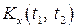 симетрична відносно своїх аргументів, тобто
симетрична відносно своїх аргументів, тобто 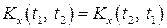 .
.
Ця властивість безпосередньо випливає з означення кореляційної функції.
3. Якщо до випадкового процесу додати невипадкову функцію 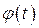 , то кореляційна функція не зміниться.
, то кореляційна функція не зміниться.
Обґрунтуємо це твердження. Нехай випадковий процес дорівнює
|
|
|
 ;
; 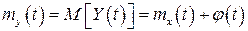 .
.
Віднімаючи 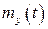 від
від 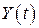 , одержимо
, одержимо
 .
.
Отже,

 .
.
4. Кореляційна функція випадкового процесу  є невід’ємно визначеною, тобто для будь-якого натурального
є невід’ємно визначеною, тобто для будь-якого натурального  , будь-яких
, будь-яких 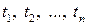 з множини
з множини 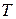 та будь-яких дійсних чисел
та будь-яких дійсних чисел 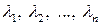 виконується нерівність
виконується нерівність
 . (28)
. (28)
Дана властивість є простим наслідком рівності (24) та відомих властивостей математичного сподівання:

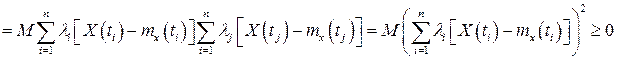 .
.
Замість кореляційної функції може розглядатися безрозмірна нормована кореляційна функція.
Означення. Нормованою кореляційною функцією випадкового процессу  називається функція
називається функція
 , (29)
, (29)
тобто коефіцієнт кореляції перерізів  і
і 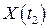 .
.
Наступні властивості нормованої кореляційної функції є простими наслідками властивостей функції 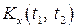 та коефіцієнта кореляції: 1)
та коефіцієнта кореляції: 1)  ; 2)
; 2) 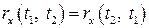 ; 3)
; 3) 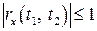 .
.
Розглянемо систему з 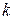 випадкових процесів
випадкових процесів
 . (30)
. (30)
Кожна з функцій цієї системи характеризується математичним сподіванням і кореляційною функцією. Однак необхідно ще ввести характеристику зв’язку між окремими випадковими величинами системи (30). Такою характеристикою є взаємна кореляційна функція будь-яких двох випадкових процесів 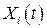 та
та  , що належать системі (30).
, що належать системі (30).
Означення. Взаємною кореляційною функцією випадкових процесів 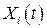 та
та  називається функція
називається функція
 , (31)
, (31)
де  ;
;  ,
, 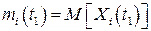 ,
, 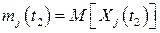
Для того, щоб відрізняти взаємну кореляційну функцію від кореляційної функції останню називають також автокореляційною функцією.
Означення. Два випадкових процеси 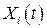 та
та  називають некорельованими, якщо їх взаємна кореляційна функція тотожно дорівнює нулю, тобто
називають некорельованими, якщо їх взаємна кореляційна функція тотожно дорівнює нулю, тобто
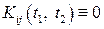 . (32)
. (32)
У ряді випадків зручно ввести безрозмірну характеристику зв’язку між випадковими процесами – нормовану взаємну кореляційну функцію
 , (33)
, (33)
де
 ,
,
 .
.
Властивості функції  легко описати, виходячи з властивостей автокореляційної функції.
легко описати, виходячи з властивостей автокореляційної функції.
Існують випадкові процеси, властивості яких залишаються інваріантними (незмінними) при будь-яких переміщеннях вздовж осі часу. Такі процеси називаються стаціонарними. Розрізняють два види стаціонарності: у вузькому розумінні та широкому розумінні.
Означення. Випадковий процес  називається стаціонарним у вузькому розумінні, якщо для будь-якого натурального
називається стаціонарним у вузькому розумінні, якщо для будь-якого натурального  і для будь-яких
і для будь-яких  ,
,  -вимірна функція розподілу
-вимірна функція розподілу  процесу
процесу  задовольняє умову
задовольняє умову
|
|
|
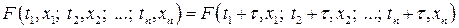 . (34)
. (34)
Умова (34) при 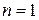 приймає вигляд
приймає вигляд
 .
.
Покладаючи  , маємо
, маємо
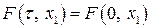 (35)
(35)
тобто всі (для будь-яких 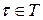 ) одновимірні розподіли є такі самі, як і розподіл в момент часу
) одновимірні розподіли є такі самі, як і розподіл в момент часу 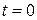 . Це означає, що одновимірні розподіли є незалежними від часу
. Це означає, що одновимірні розподіли є незалежними від часу 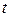 .
.
Умова (35) при  має вигляд
має вигляд
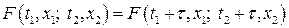
Покладаючи  , маємо
, маємо
 , (36)
, (36)
тобто всі двовимірні розподіли (для будь-яких 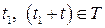 ) є такі самі, як і двовимірний розподіл в моменти часу
) є такі самі, як і двовимірний розподіл в моменти часу  . Отже, двовимірний розподіл при значеннях аргументів
. Отже, двовимірний розподіл при значеннях аргументів 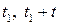 залежить лише від
залежить лише від 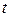 і не залежить від
і не залежить від  .
.
Що означає стаціонарність у вузькому розумінні з практичної точки зору? Для прикладу уявимо собі часовий ряд, який характеризує процес випуску продукції. Тут стаціонарність у вузькому розумінні означає, що систематичним змінам не підлягають ані умови виготовлення продукції, ані сировина та напівфабрикати, які постачаються ззовні, ані будь-які інші фактори, існує можливість появи тільки деяких випадкових змін, і то лише таких, що їх розподіли не змінюються при будь-яких переміщеннях вздовж часової осі. З іншого боку, такі процеси, наприклад, як температура, ціна іноземної валюти, які спостерігаються протягом деякого періоду часу 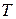 є, очевидно, нестаціонарними випадковими процесами.
є, очевидно, нестаціонарними випадковими процесами.
Припустимо тепер, що  – стаціонарний у вузькому розумінні процес і
– стаціонарний у вузькому розумінні процес і  . Зауважимо, що остання умова забезпечує існування для випадкового процесу
. Зауважимо, що остання умова забезпечує існування для випадкового процесу  моментів першого та другого порядків. Тоді з (35) випливає, що
моментів першого та другого порядків. Тоді з (35) випливає, що
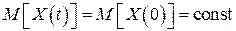 , (37)
, (37)
а з (36) випливає, що
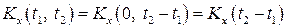 . (38)
. (38)
Як бачимо, момент першого порядку, визначений рівністю (37), не залежить від 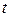 . Його можна позначити просто
. Його можна позначити просто 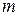 . Момент другого порядку залежить лише від
. Момент другого порядку залежить лише від  . Його можна назвати автоковаріацією порядку
. Його можна назвати автоковаріацією порядку  (кореляційною функцією) і позначити
(кореляційною функцією) і позначити 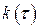 . Крім цього, позначимо
. Крім цього, позначимо  ,
,  .
.
Отже, характеристики першого та другого порядків випадкового стаціонарного процессу є такі: середнє значення 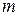 , дисперсія
, дисперсія 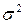 , «корелограма», яка збігається з коефіцієнтом автокореляції
, «корелограма», яка збігається з коефіцієнтом автокореляції 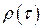 .
.
Неважко встановити, що 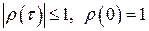 .
.
Особливо простий вигляд має корелограма так званого «чисто випадкового процессу», який за означенням утворюється послідовністю незалежних випадкових величин з одним і тим самим розподілом 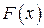 . Скінченновимірні розподіли цього процесу виражаються формулою
. Скінченновимірні розподіли цього процесу виражаються формулою
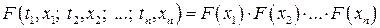 . (39)
. (39)
Зрозуміло, що цей процес стаціонарний, і для нього всі коефіцієнти автокореляції дорівнюють нулю (крім 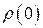 ).
).
Процеси, в яких всі 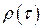 , крім
, крім 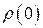 , дорівнюють нулю, називаються «процесами без кореляції».
, дорівнюють нулю, називаються «процесами без кореляції».
Ми вже відзначали, що в кореляційній теорії розглядаються моменти випадкових процесів тільки першого та другого порядків. Для властивостей, що залежать лише від характеристик першого та другого порядків, вимога стаціонарності, визначена умовою (34), є занадто жорсткою. Тому природно ввести ще одне означення стаціонарного випадкового процесу.
Означення. Випадковий процес  , для якого виконані співвідношення (37), (38), називається стаціонарним процесом в широкому розумінні.
, для якого виконані співвідношення (37), (38), називається стаціонарним процесом в широкому розумінні.
Надалі під стаціонарними випадковими процесами будемо розуміти випадкові процеси, стаціонарні в широкому розумінні.
Означення. Два стаціонарні випадкові процеси  та
та 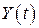 називаються стаціонарно зв’язаними, якщо їх взаємна кореляційна функція залежить тільки від різниці аргументів, тобто
називаються стаціонарно зв’язаними, якщо їх взаємна кореляційна функція залежить тільки від різниці аргументів, тобто
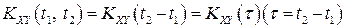 (40)
(40)
|
|
|
|
|
Дата добавления: 2014-01-04; Просмотров: 2740; Нарушение авторских прав?; Мы поможем в написании вашей работы!