Метод Зейделя

Рассмотрим на примере систем из трех уравнений:

(4.11)

Предположим, что диагональные элементы a₁₁, a₂₂, a₃₃ отличны от нуля. В противном случае нужно переставить уравнения. Выразим неизвестные x₁, x₂, x₃ соответственно из первого, второго и третьего уравнений системы (1):

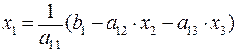, (4.12)

, (4.13)

. (4.14)

Зададим некоторые начальные (нулевые) приближения значений неизвестных:

.

Подставляя эти значения в правую часть выражения (4.12), получим новое (первое) приближение для x₁:

.

Используя это значение для x₁ (т.е. ) и приближение x₃⁽⁰⁾, находим из (4.13) первое приближение для x₂:

.

И, наконец, используя вычисленные значения x₁ = x₁⁽¹⁾ и x₂ = x₂⁽¹⁾, находим с помощью выражения (4.14) первое приближение для x₃:

.

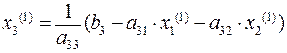На этом заканчивается первая итерация решения системы (4.12), (4.13), (4.14). Используя теперь значения x₁⁽¹⁾, x₂⁽¹⁾, x₃⁽¹⁾, можно таким же способом провести вторую итерацию. В результате нее будут найдены вторые приближения к решению: x₁ = x₁⁽²⁾, x₂ = x₂⁽²⁾, x₃ = x₃⁽²⁾. Затем выполняется третья и последующие итерации. Приближение с номером k можно представить в виде:

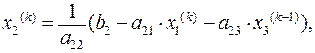
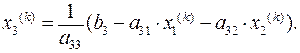
Итерационный процесс продолжается до тех пор, пока значения x₁^(k), x₂^(k), x₃^(k) не станут близкими с заданной погрешностью к значениям x₁^(k-1), x₂^(k-1), x₃^(k-1). Т.е. вычисляется параметр

.

Если

δ < ε, (4.15)

то процесс прекращается. Величина ε > 0. Это малое, заданное в исходных данных число; ε – погрешность вычисления. Обычно ε = 10^-2…10^-5.

Условия сходимости итерационного процесса рассматривать не будем. Во избежание непроизводительных затрат машинного времени в алгоритм вводят счетчик числа итераций. Если процесс сходится, то вычисления прекращаются при выполнении условия (4.15). Если не сходится, то вычисления прекращаются при достижении числа итераций k некоторого заданного значения M. Число M достаточно большое: M ≥ 500.

Отметим, что для того, чтобы процесс итерационных вычислений сошелся (если он не сходится), можно поменять начальные приближения x_i⁽⁰⁾.

Дата добавления: 2014-01-04