О многочленах наилучших равномерных приближений

Резюмируя исследования предыдущего параграфа, в частности, анализируя неравенство (18.3), можно хотя бы частично ответить на вопрос о сходимости последовательности интерполяционных многочленов Лагранжа L_n (x) к функции f (x) на отрезке [ а, b ]. Для которой они построены:

если функция f (x) бесконечно дифференцируема на [ а, b ] и в качестве узлов интерполяции берутся корни многочленов Чебышева (приведенные к отрезку [ а, b ], то

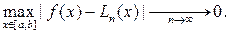
Чебышевской нормой функции f (x) в пространстве С [ а, b ] непрерывных на [ а, b ] функций называется

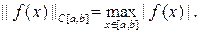
Для достаточно гладких функций f (x) при специальном расположении узлов интерполяции последовательность интерполяционных многочленов Лагранжа L_n (x) (построенных по точным значениям функции f (x) сходится к f (x) по норме Чебышева; другими словами, имеет место равномерная сходимость последовательности L_n (x) (к f x).

Обобщением установленного факта для непрерывных (не обязательно дифференцируемых) функций и произвольных (не обязательно интерполяционных) многочленов является широко известная в математическом анализе теорема.

Теорема 18.1 (Вейерштрасса). Для любой непрерывной на [ а, b ] функции f (x) найдется такой многочлен Q_n (x), что

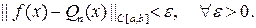
Как следует из теоремы Вейерштрасса, если отказаться от того, чтобы аппроксимирующий функцию многочлен Q_n (x) степени п был интерполяционным, от f (x) достаточно потребовать непрерывность на [ а, b ], чтобы за счет повышения степени многочдена при надлежащем подборе его коэффициентов величина чебышевской нормы могла быть сделанной сколь угодно малой, иначе, чтобы качество аппроксимации функции f (x) многочленом Q_n (x) на отрезке [ а, b ] было сколь угодно хорошим в смысле чебышевской метрики.

Если степень п аппроксимирующего f (x) многочлена Q_n (x) зафиксировать и распоряжаться только его коэффициентами, то в общем случае величину нельзя сделать сколь угодно малой. Однако доказано, что для любой функции f (x)ÎС[ а, b ] существует единственный такой многочлен Q_n (x), который из всех многочленов степени и наилучшим образом аппроксимирует на [ а, b ] функцию f(x), минимизируя максимальное расстояние между f (x) и Q_n (x). Этот многочлен, т.е. многочлен , такой, что

называется многочленом наилучшего равномерного приближения для f (x) на [ а, b ] или ее чебышевским приближением.

К сожалению, неизвестны ни общий вид многочленов наилучших равномерных приближений, ни способы их построения. Имеются лишь некоторые методики построения многочленов, близких к наилучшим равномерным, а также способы построения чебышевских приближений невысокого порядка для нескольких весьма узких классов функций. Последние существенно опираются на приведенную теорему о чебышевском альтернансе, что демонстрируется в следующих двух простейших случаях.

Дата добавления: 2014-01-04