Структура общего решения однородной системы линейных уравнений

Рассмотрим однородную систему линейных уравнений с прямоугольной матрицей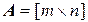

(4.3.1)

Теорема 4.3.1. Для того чтобы система (4.3.1) имела ненулевое решение необходимо и достаточно, чтобы выполнялось условие .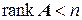

Доказательство. Необходимость. Пусть система (4.3.1) имеет ненулевое решение 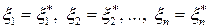. Тогда , следовательно, столбцы 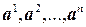линейно зависимы, отсюда .

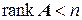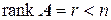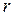Достаточность. Предположим, что . В матрице системы существует ровно линейно независимых столбцов, образующих столбцовый базис матрицы . Пусть для определенности столбцы 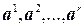образуют указанный базис. Тогда любой другой столбец , представим в виде их линейной комбинации

, ,

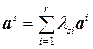отсюда имеем равенство . Это означает, что столбец

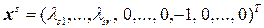, (4.3.2)

где «–1» стоит на s- ом месте, , является ненулевым решением системы (4.3.1).

Заметим, что решения ,в силу последних элементов являются линейно независимыми, причем для любых чисел 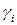, столбец также является решением однородной системы (4.3.1).

Следствие 4.3.1. Любое решение однородной системы (4.3.1) представимо в виде линейной комбинации решений 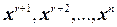, где .

Доказательство. По условию имеем . Предполагая линейную независимость столбцов 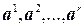, получаем линейно независимых решений ,системы (4.3.1). Допустим, что — произвольное нетривиальное решение.

Построим столбец

.

Ясно, что 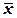— решение системы (4.3.1) как сумма решений, причем с учетом (4.3.2)

,

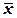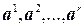где , . Поскольку — решение, то , но столбцы линейно независимы, поэтому 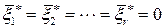, отсюда .

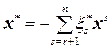Определение 4.3.1. Линейно независимые решения ,системы (4.3.1), через которые можно выразить любое другое решение этой системы, называется фундаментальной системой решений.

Определение 4.3.2. Решение системы (4.3.1) вида

,

где 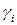— произвольные постоянные, а ,— фундаментальная система решений, называется общим решением однородной системы линейных уравнений.

Дата добавления: 2014-01-05