Линейная зависимость и независимость векторов

Пусть L — произвольное линейное пространство, a _i Î L, — его элементы (векторы).

Определение 3.3.1. Выражени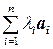е , где 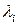, — произвольные вещественные числа, называется линейной комбинацией векторов a₁, a₂,…, a _n.

Если вектор р = 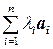, то говорят, что р разложен по векторам a₁, a₂,…, a _n.

Определение 3.3.2. Линейная комбинация векторов называется нетривиальной, если среди чисел 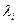есть хотя бы одно отличное от нуля. В противном случае, линейная комбинация называется тривиальной.

Определение 3. 3.3. Векторы a₁, a₂,…, a _n называются линейно зависимыми, если существуют их нетривиальная линейная комбинация, такая что

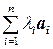= 0.

Определение 3. 3.4. Векторы a₁,a₂,…, a _n называются линейно независимыми, если равенство 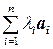= 0 возможно лишь в случае, когда все числа l 1, l 2,…, l_n одновременно равны нулю.

Отметим, что всякий ненулевой элемент a₁ можно рассматривать как линейно независимую систему, ибо равенство l a₁ = 0 возможно лишь при условии l = 0.

Теорема 3.3.1. Необходимым и достаточным условием линейной зависимости a₁, a₂,…, a _n является возможность разложения, по крайней мере, одного из этих элементов по остальным.

Доказательство. Необходимость. Пусть элементы a₁, a₂,…, a _n линейно зависимы. Это означает, что 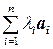= 0, причем хотя бы одно из чисел l 1, l 2,…, l_n отлично от нуля. Пусть для определенности l 1 ¹ 0. Тогда

= 0 ,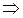

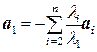т. е. элемент a₁ разложен по элементам a₂, a₃, …, a _n.

Достаточность. Пусть элемент a₁ разложен по элементам a₂, a₃, …, a _n, т. е. a₁ = 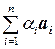. Тогда 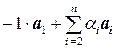= 0, следовательно, существует нетривиальная линейная комбинация векторов a₁, a₂,…, a _n, равная 0, поэтому они являются линейно зависимыми.

Теорема 3.3.2. Если хотя бы один из элементов a₁, a₂,…, a _n нулевой, то эти векторы линейно зависимы.

Доказательство. Пусть a _n = 0, тогда 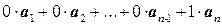= 0, что и означает линейную зависимость указанных элементов.

Теорема 3.3.3. Если среди n векторов какие-либо p (p < n) векторов линейно зависимы, то и все n элементов линейно зависимы.

Доказательство. Пусть для определенности элементы a₁, a₂,…, a _p линейно зависимы. Это означает, что существует такая нетривиальная линейная комбинация, что 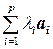= 0. Указанное равенство сохранится, если добавить к обеим его частям элемент 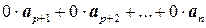. Тогда 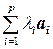+ 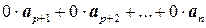= 0, при этом хотя бы одно из чисел l 1, l 2,…, lp отлично от нуля. Следовательно, векторы a₁, a₂,…, a _n являются линейно зависимыми.

Следствие 3.3.1. Если n элементов линейно независимы, то любые k из них линейно независимы (k < n).

Теорема 3.3.4. Если векторы a₁, a₂,…, a _{n- 1} линейно независимы, а элементы a₁, a₂,…, a _{n- 1}, a _nлинейно зависимы, то вектор a _nможно разложить по векторам a₁, a₂,…, a _{n- 1}.

Доказательство. Так как по условию a₁, a ₂,…, a _{n- 1}, a _n линейно зависимы, то существует их нетривиальная линейная комбинация 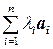= 0, причем (в противном случае, окажутся линейно зависимыми векторы a₁, a₂,…, a _{n- 1}). Но тогда вектор

,

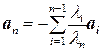что и требовалось доказать.

Дата добавления: 2014-01-05