Кинематические цепи. Механизмы

Кинематической цепью называется связанная система звеньев, образующих между собой кинематические пары.

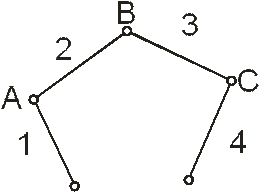
Кинематические цепи подразделяются на плоские и пространственные. В плоских цепях все звенья перемещаются либо в одной, либо в параллельных плоскостях. Все другие цепи будут пространственными. Кинематические цепи могут быть открытыми и замкнутыми (рис. 2).

a	б

Рис. 2 Кинематические цепи (а -открытая; б -замкнутая)

Число степеней свободы, т.е. суммарное число независимых перемещений звеньев кинематической цепи определяется по ее структурной формуле, которую несложно вывести. В самом общем случае кинематическая цепь может состоять из n подвижных звеньев, которые образуют между собой и с неподвижным звеном p ₁ кинематических пар 1-го, p ₂ пар 2-го, p ₃ пар 3-го, p ₄ пар 4-го и p ₅ пар 5-го классов. До соединения в кинематическую цепь все звенья имели 6n степеней свободы. При образовании кинематической цепи кинематические пары будут накладывать на относительное движение звеньев условия связи. При этом пара 1-го класса накладывает 1 связь, 2-го класса – 2 связи, 3-го класса – 3 связи, 4-го класса – 4 связи и 5-го класса – 5 связей. Тогда суммарное число степеней свободы всех звеньев кинематической цепи можно определить по формуле:

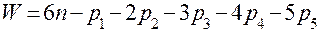(1)

Выражение (1) носит название структурной формулы, а число W – числа степеней подвижности.

Механизмом называется кинематическая цепь, в которой при заданном законе движения одного или нескольких звеньев, все остальные звенья будут перемещаться по вполне определенным законам.

В каждом механизме имеется 3 характерных типов звеньев.

1. Неподвижное звено-стойка. В любом механизме имеется одна стойка, т.к. все неподвижные звенья связаны между собой.

2. Ведущие звенья – те, закон движения которых задается предварительно. Так как этот закон может быть задан произвольно, то число степеней подвижности механизма W всегда должно быть равно числу ведущих звеньев, ввиду того, что они определяют число независимых движений в механизме.

3. Ведомые звенья, закон движения которых полностью зависит от закона движения ведущих. Независимых движений они иметь не могут.

Кинематические пары накладывают на относительное движение звеньев некоторые ограничения, которые могут оказаться общими для всех звеньев механизма.

В зависимости от этого общего числа условий связи различают семейства механизмов. Для каждого семейства существует своя структурная формула, вытекающая из выражения (1), являющегося структурной формулой механизма нулевого семейства, т.к. в нем отсутствуют общие условия связи. Для механизмов первого семейства структурная формула имеет вид:

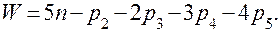
Общее число степеней свободы всех звеньев в этом случае не 6 n, а 5 n, т.к. одно перемещение запрещено. У кинематических пар число связей на единицу меньше, т.к. одна общая связь учтена в первом члене формулы. Кинематических пар 1-го класса в таких механизмах быть не может.

Рассуждая подобным образом, запишем структурные формулы для механизмов остальных семейств:

2-го семейства
3-го семейства
4-го семейства
5-го семейства
т.е. механизмы 5-го семейства являются парами 5-го класса.

Плоские механизмы относятся к 3-му семейству, т.к. движение звеньев в одной или параллельных плоскостях исключает их перемещение вдоль одной координатной оси и вращение относительно двух осей. Для них справедлива формула, которая была предложена академиком П.Л. Чебышевым в 1869 году и носит его имя. Часто формулу П.Л. Чебышева записывают в следующем виде:

где	Pн – число низших кинематических пар;
Pв – число высших кинематических пар.

Дата добавления: 2014-01-05