Сложение перпендикулярных колебаний. Фигуры Лиссажу

Биения

Сложение гармонических колебаний одного направления.

Рассмотрим колебательную систему с одной степенью свободы, состояние которой определяется зависимостью некоторой величины 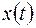от времени. Пусть колебание в этой системе представляет собой сумму двух гармонических колебаний с одинаковой частотой 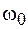, но различными амплитудами и начальными фазами, т. е.

.

Так как "смещение" колебательной системы от положения равновесия происходит вдоль одного единственного "направления", то в этом случае говорят о сложении гармонических колебаний одного направления. На векторной диаграмме складываемые колебания изобразятся в виде двух векторов и 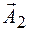, повернутых относительно друг друга на угол (рис. 6.1). Так как частоты складываемых колебаний одинаковы, то их взаимное положение будет оставаться неизменным в любой момент времени, и результирующее колебание будет изображаться вектором, равным сумме векторов и 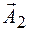. Складывая векторы по правилу параллелограмма и используя теорему косинусов, получим

, (6.1)

где

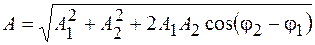, (6.2)

. (6.3)

Таким образом, при сложении двух гармонических колебаний одного направления с одинаковыми частотами получается гармоническое колебание той же частоты, амплитуда и начальная фаза которого определяются выражениями (6.2), (6.3).

Два гармонических колебания, которые совершаются с одинаковой частотой и имеют постоянную разность фаз, называются когерентными. Следовательно, при сложении когерентных колебаний получается гармоническое колебание той же частоты, амплитуда и начальная фаза которого определяются амплитудами и начальными фазами складываемых колебаний.

Если складываемые колебания имеют разные частоты и 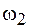, но одинаковые амплитуды 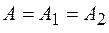, то, используя известное из тригонометрии выражение для суммы косинусов двух углов, получим

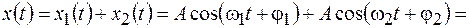
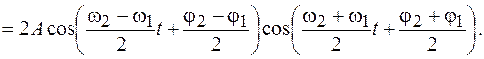(6.4)

Из полученного выражения видно, что результирующее колебание не является гармоническим.

Пусть частоты складываемых колебаний близки друг к другу так, что 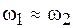и . Этот случай называется биением двух частот.

Обозначив 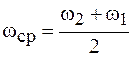, и , можно записать

. (6.5)

Из выражения (6.5) следует, что результирующее колебание можно представить как гармоническое колебание с некоторой средней частотой , амплитуда которого медленно (с частотой ) меняется во времени. Время 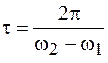называется периодом биений, а – частотой биений. График биений изображен на рисунке 6.2. Биения возникают при одновременном звучании двух камертонов одинаковой тональности. Их можно наблюдать с помощью осциллографа при сложении гармонических колебаний двух генераторов, настроенных на одну частоту. В обоих случаях частоты источников колебаний будут немного различаться, в результате чего возникнут биения.

Так как колебания происходят с разными частотами, то разность фаз складываемых колебаний изменяется во времени, следовательно, колебания не являются когерентными. Изменение во времени амплитуды результирующих колебаний является характерным следствием некогерентности складываемых колебаний.

Сложение колебаний очень часто наблюдается в электрических цепях и, в частности, в радиотехнических устройствах связи. В одних случаях это делается целенаправленно, чтобы получить сигнал с заданными параметрами. Так, например, в гетеродинном приемнике принимаемый сигнал складывается (смешивается) с сигналом гетеродина, чтобы в результате последующей обработки получить колебание промежуточной частоты. В других случаях сложение колебаний происходит самопроизвольно, когда на вход устройства кроме полезного сигнала поступает какая-либо помеха. По сути, все многообразие формы электрических сигналов представляет собой результат сложения двух или большего числа гармонических колебаний.

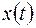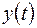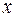Если колебательная система имеет две степени свободы, то ее состояние характеризуется двумя независимыми величинами и , т. е. некоторой точкой на плоскости . Так как координаты и меняются во времени, то точка совершает движение по плоскости . Простейший пример такой системы приведен на рисунке 7.1. 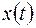Колебания груза на пружинах могут происходить в двух взаимно перпендикулярных направлениях, поэтому движение груза представляет собой сложение двух перпендикулярных колебаний и .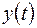

Рассмотрим случай, когда 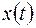и 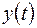изменяются с одной и той же частотой 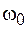и имеют разность фаз 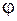. Если начало отсчета времени выбрать так, чтобы начальная фаза колебания 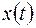равнялась нулю, то складываемые перпендикулярные колебания можно записать в виде

(7.1)

Уравнения (7.1) определяют траекторию движения точки на плоскости в параметрической форме. Чтобы получить явное выражение для траектории, необходимо исключить из системы уравнений (7.1) время . Из аналитической геометрии известно, что в общем случае получается уравнение эллипса, у которого размеры полуосей и их наклон по отношению к координатным осям определяются амплитудами , 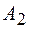и разностью фаз 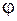. Рассмотрим некоторые частные случаи:

а) .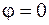

Используя формулы приведения для тригонометрических функций, легко показать, что 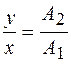. Отсюда следует, что траектория движения точки представляет собой прямую (рис. 7.2, а), проходящую через первый и третий квадранты и образующую с осью угол 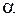, определяемый соотношением

;

б) .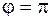

Аналогично предыдущему случаю можно сделать вывод, что траектория движения точки представляет собой прямую , проходящую через второй и четвертый квадранты (рис. 7.2, б) и образующую с осью угол 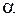, определяемый соотношением

;

в) .

В этом случае уравнения (7.1) принимают вид

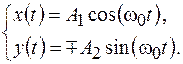
Независимо от знака 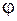эти уравнения после исключения времени дают уравнение эллипса, полуоси которого совпадают с осями координат:

.

Если разность фаз 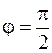, то движение точки по эллипсу происходит по часовой стрелке (рис. 7.2, в). При изображающая точка движется против часовой стрелки (рис. 7.2, г).

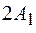Если частоты перпендикулярных колебаний не равны, то результат их сложения не столь однозначен. При произвольном соотношении частот траектория движения изображающей точки не может быть представлена в виде какой-либо замкнутой линии, а будет сплошь заполнять на плоскости прямоугольник со сторонами и 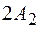. Движение точки по устойчивой замкнутой траектории будет происходить лишь в том случае, если частоты складываемых колебани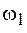й и относятся как простые целые числа, т. е. . Получающиеся при этом фигуры называются фигурами Лиссажу.

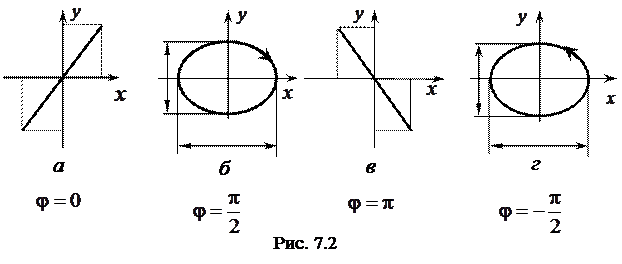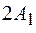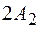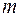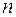Примеры фигур Лиссажу приведены на рисунке 7.3. Каждая фигура вписана в прямоугольник со сторонами и , причем числа касаний фигурой Лиссажу сторон прямоугольника равны и . Фигуры Лиссажу можно наблюдать на экране осциллографа, если на вертикальные и горизонтальные отклоняющие пластины подать напряжения, пропорциональные соответственно 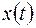и .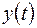

Форма фигур Лиссажу зависит от разности начальных фаз колебаний. Наблюдение фигур Лиссажу используется для сравнения частот и разности фаз двух гармонических колебаний.

Дата добавления: 2014-01-05