Диагонализируемые преобразования

Линейное преобразование называется диагонализируемым, если существует базис, в котором матрица линейного преобразования имеет диагональный вид. Заметим, что базис, в котором матрица линейного преобразования имеет диагональный вид, образован собственными векторами. Верно и обратное. В базисе из собственных векторов матрица линейного преобразования имеет диагональный вид. Не каждое линейное преобразование диагонализируемо. Например, линейное преобразование, заданное матрицей не диагонализируемо.

Теорема 7.3. Собственные векторы, отвечающие различным собственным значениям, линейно независимы.

Доказательство. Пусть - линейно независимая система собственных векторов, соответствующих собственному значению , где i =1,…, s. Покажем линейную независимость системы векторов индукцией по s. При s =1 утверждение очевидно. Пусть оно верно для s -1. Покажем его справедливость для s. Допустим, система - линейно зависима. Тогда найдутся коэффициенты не все равные нулю, что 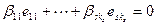. Из этого равенства выводим 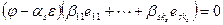или 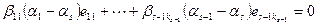. По предположению индукции все коэффициенты в этом равенстве равны 0, и, значит при i < s. Но тогда система 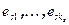- линейно зависима, что противоречит условиям теоремы. К полученному противоречию привело допущение о линейной зависимости системы векторов , значит, эта система линейно независима, что и требовалось доказать.

Рассмотрим вопрос о количестве линейно независимых собственных векторов, соответствующих собственному числу .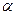

Геометрической кратностью собственного числа 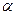называется дефект преобразования 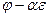, а алгебраической кратностью называется кратность корня 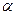в характеристическом многочлене.

Теорема 7.4. Геометрическая кратность 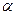не превосходит его алгебраической кратности.

Доказательство. Пусть геометрическая кратность 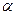равна k. Дополним базис 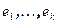ядра преобразования 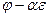до базиса всего пространства 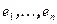. Матрица линейного преобразования в этом базисе имеет вид и характеристический многочлен равен . Таким образом, алгебраическая кратность 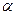не меньше геометрической кратности, что и требовалось доказать.

Теорема 7.5 Линейное преобразование 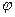линейного пространства V над числовым полем P диагонализируемо тогда и только тогда, когда характеристический многочлен раскладывается над полем P на линейные множители и алгебраическая кратность каждого корня совпадает с его геометрической кратностью.

Доказательство очевидно.

Дата добавления: 2014-01-05