Определения направленного отрезка и вектора

Векторы на плоскости и в пространстве

Определение 1. Направленным отрезком называется упорядоченная пара точек (на плоскости или в трёхмерном пространстве).

Если даны две точки A и B (рассматриваемые именно в этом порядке), то соответ­ствующий направленный отрезок будем обозначать (A, B). Отрезок (в обычном смысле), соединяющий точки A и B, будем обозначать AB. Я не исключаю случая, когда A = B (т. е. можно рассматривать направленный отрезок вида (A, A)). В этом случае отрезок AB пре­вращается в точку. Упорядоченность пары означает, что направленные отрезки (A, B) и (B, A) считаются различными, если A ≠ B.

Определение 2. В направленном отрезке (A, B) точка A называется началом, а точка B − концом.

В направленном отрезке (A, A) начало совпадает с концом.

Определение 3. Направленный отрезок, начало которого совпадает с концом, на­зывается нулевым направленным отрезком.

Определение 4. Если A ≠ B, то (единственную) прямую, проходящую через точки A и B, будем называть несущей прямой (направленного отрезка (A, B)).

В случае A = B несущая прямая не определена однозначно.

Определение 5. Два направленных отрезка (A, B) и (C, D) называются эквивалент­ными (обозначение: (A, B) ~ (C, D)), если

1. Их несущие прямые параллельны или совпадают.

2. Длины соответствующих отрезков равны (| AB| = |CD|).

3. Данные направленные отрезки сонаправленны.

Если хотя бы один из направленных отрезков нулевой, то надо опустить первый и третий пункты (можно считать, что они в этом случае всегда выполняются).

Для любителей математической строгости приведу другой вариант определения эквивалентности направленных отрезков, вполне равносильный первому[1]. Он не содержит интуитивного и трудно аксиоматизируемого понятия сонаправленности. Введём такое обозначение: если даны две точки A и B, то середину отрезка, соединяющего точки A и B, будем обозначать med AB (если точки A и B совпадают, то med AB = A)[2].

Определение 6. Два направленных отрезка (A, B) и (C, D) называются эквивалент­ными, если med AD = med BC.

Упражнение. Докажите эквивалентность (равносильность) этих двух определений.

Определение 7. Множество всех направленных отрезков, эквивалентных какому-нибудь одному, называется вектором.

Ясно, что все направленные отрезки из этого множества можно получить из дан­ного с помощью сдвига, или параллельного переноса.

Векторы будем обозначать латинскими курсивными буквами со стрелками, напри­мер, 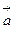. В печатных текстах принято другое обозначение − латинскими курсивными бук­вами, выделяемыми полужирным шрифтом (иногда тоже стрелками без выделения), на­пример, a. (Я буду здесь так же выделять обозначение вектора полужирным шрифтом.) Если же надо обозначить вектор, соответствующий направленному отрезку (A, B) (т. е. множество всех направленных отрезков, ему эквивалентных), то пользуются другим обо­значением: .

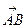Предложение. Нулевой направленный отрезок эквивалентен другому направлен­ному отрезку тогда и только тогда, когда второй отрезок также нулевой.

Доказательство. Это очевидное следствие любого из двух определений.

Определение 8. Множество всех направленных отрезков, эквивалентных какому-нибудь (а следовательно, и любому) нулевому, называется нулевым вектором и обознача­ется 0.

Дата добавления: 2014-01-05