
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Обыкновенные дифференциальные уравнения
|
|
|
|
В системе MatLab предусмотрены специальные средства решения задачи Коши для системобыкновенных дифференциальных уравнений, заданных как в явной форме  = F(t,x), так и в неявной M
= F(t,x), так и в неявной M =F(t,x), где М- матрица, - т.н. решатель ОДУ (solver ODE), обеспечивающий пользователю возможность выбора метода, задания начальных условий и др.
=F(t,x), где М- матрица, - т.н. решатель ОДУ (solver ODE), обеспечивающий пользователю возможность выбора метода, задания начальных условий и др.
В простейшем варианте достаточно воспользоваться командой [T,X]=solver('F', [DT], X0,...), где DT - диапазон интегрирования, X0 - вектор начальных значений, F - имя функции вычисления правых частей системы, solver - имя используемой функции (ode45 - метод Рунге-Кутта 4 и 5-го порядков, ode23 - тот же метод 2 и 3-го поряд-ков, ode113 - метод Адамса - для нежестких систем, ode23s, ode15s - для жестких систем и др.). Версии решателя различаются используемыми методами (по умолчанию относительная погрешность 10-3 и абсолютная 10-6) и соответственно временем и успешностью решения. Под жесткостью здесь понимается повышенное требование к точности - использование минимального шага во всей области интегрирования. При отсутствии информации о жесткости рекомендуется попытаться получить решение посредством ode45 и затем ode15s. Если диапазон DT задан начальным и конечным значением [to, tk], то количество элементов в массиве Т (и в массиве решений Х) определяется необходимым для обеспечения точности шагом; при задании DT в виде [to, t1, t2,..., tk] или [to:Dt: tk] - указанными значениями.
Например, в простейшем варианте решение уравнения  =tЧe-t в интервале t О[0, 0.5] с начальным условием x(t=0)=1:
=tЧe-t в интервале t О[0, 0.5] с начальным условием x(t=0)=1:
| function f =odu1(t,x) | |||||||||
| f=t*exp(-t); | |||||||||
| >> [T,X]=ode45 ('odu1', [0, 0.5], 1) | |||||||||
| T = | 0.0125 | 0.0250 | 0.0375 | 0.0500 | 0.0625 | 0.0750 | 0.0875 | ||
| 0.1000 | 0.1125 | 0.1250 | 0.1375 | 0.1500 | 0.1625 | 0.1750 | … | ||
| X = | 1.0000 | 1.0000 | 1.0003 | 1.0006 | 1.0012 | 1.0018 | 1.0027 | 1.0036 | |
| 1.0046 | 1.0058 | 1.0072 | 1.0086 | 1.0102 | 1.0118 | 1.0136 | …. |
Для иллюстрации решения системы и ряда нестандартных возможностей рассмотрим задачу выравнивания цен по уровню актива в следующей постановке.
|
|
|
Предположим, что изменение уровня актива у пропорционально разности между предложением s и спросом р, т.е. y'=k(s-d), k>0, и что изменение цены z пропорционально отклонению актива у от некоторого уровня y0, т.е. z'=-m(y-y0), m>0. Естественно, что предложение и спрос зависят от цены, например, s(z)=az+s0, d(z)= d0 - cz. Соответственно возникает система дифференциальных уравнений
y' = kЧ(s(z)-d(z))
z' = - mЧ (y-y0).
Вычисление правых частей оформляем функцией:
function f=odu2(t,X) y=X(1); z=X(2); a=20; c=10; s0=10; d0=50; k=0.3; m=0.1; s=a*z+s0; d= d0-c*z; y0=19; f(1)=k*(s-d); f(2)=-m*(y-y0); f=f'; % вектор-столбецЕсли выполнить решение при y0 = 19, z0 =2
>> [T,Y]=ode45('odu2', [0:0.3:9],[ 19 2 ]); >> [T Y] >> plot(T,Y)будет выведена таблица значений искомых функций:
ans = 0 19.0000 2.0000 0.3000 20.7757 1.9731 0.6000 22.4101 1.8949 0.9000 23.7686 1.7714 1.2000 24.7427 1.6126 1.5000 25.2569 1.4313...и их графики (рис. 8.6).
Эта система уравнений относится к числу т.н. автономных (или динамических), ибо независимая переменная в нее явно не входит; соответственно может быть установлена связь между найденными решениями: в параметрическом задании линия y=y(t), z=z(t) определяет фазовую кривую (траекторию) системы - гладкую кривую без самопересечений, замкнутую кривую или точку, которая позволяет судить об устойчивости системы.
Так, установив опции к построению двумерного фазового портрета (функция odephas2)и номера переменных состояния:
>> opt=odeset('OutputSel',[1 2], 'OutputFcn','odephas2');
>> [T,Y]=ode45('odu2', [0:0.3:9],[19 2],opt);
получаем фазовый портрет системы, свидетельствующий о ее устойчивости - гармонии между активом и ценами (рис.8.7).
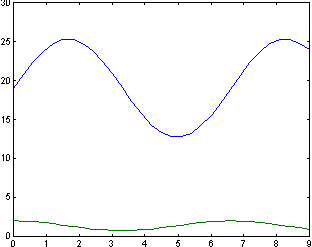 Рис.8.6 Рис.8.6
| 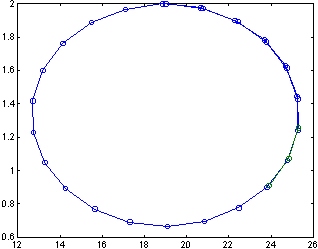 Рис.8.7 Рис.8.7
|
В качестве другого примера подобных задач рассмотрим известную задачу динамики популяций, где рассматривается модель взаимодействия "жертв" и "хищников", в которой учитывается уменьшение численности представителей одной стороны с ростом численности другой. Модель была создана для биологических систем, но с определенными корректурами применима к конкуренции фирм, строительству финансовых пирамид, росту народонаселения, экологической проблематике и др.
|
|
|
Эта модель Вольтерра-Лотка с логистической поправкой описывается системой уравнений
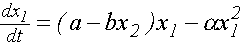
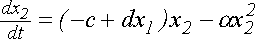
с условиями заданной численности "жертв" и "хищников" в начальный момент t=0.
Решая эту задачу при различных значениях a, получаем различные фазовые портреты (обычный колебательный процесс и постепенная гибель популяций).
function f=VolterraLog(t,x) a=4; b=2.5; c=2; d=1; alpha=0.1; f(1)= (a-b*x(2))*x(1)-alpha*x(1)^2; f(2)= (-c+d*x(1))*x(2)-alpha*x(2)^2; f=f';>>opt=odeset('OutputSel',[1 2], 'OutputFcn', 'odephas2');
>> [T,X]=ode45('VolterraLog', [0 10],[3 1],opt);
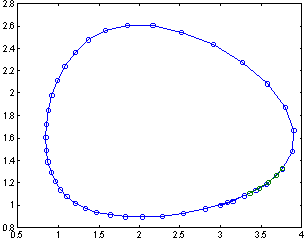 Рис.8.8 (a =0) Рис.8.8 (a =0)
|  Рис.8.9 (a =0.1) Рис.8.9 (a =0.1)
|
Имеется возможность построения и трехмерного фазового портрета с помощью функции odephas3. Например, решение задачи Эйлера свободного движения твердого тела:
 =x2x3,
=x2x3,
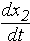 =-x1x3,
=-x1x3,
 =-0.51Чx1x2
=-0.51Чx1x2
выступает в виде:
function f=Eiler(t,x) f(1)= x(2)*x(3); f(2)= -x(1)*x(3); f(3)= -0.51*x(1)*x(2); f=f';| >> opt=odeset('OutputSel',[1 2 3], 'OutputFcn', 'odephas3'); >> [T,X]=ode45('Eiler', [0 7.25], [0 0 1], opt); %рис.8.10 >> [T,X]=ode45('Eiler', [0:0.25:7.25],[0 1 1]); | |
| >> plot(T,X) | % рис.8.11 |
 Рис.8.10. Рис.8.10.
|  Рис.8.11. Рис.8.11.
|
наверх
следующая глава