Понятие графических объектов и их параметров

Если вы создаете объект-примитив, например сферу, то вызывается функция, которая запрашивает у вас набор данных, характеризующих сферический объект. Запишем эту функцию в следующем виде:

СФЕРА (О, R, n, m, М), (1)

где СФЕРА – название функции (в данном случае название графического объекта); О, R, n, m, М – набор данных о сфере: О – координаты центра сферы, R – радиус сферы, n - число продольных сегментов при построении сеточной графической модели (вдоль параллелей как на рис. 1); m - число поперечных сегментов при построении сеточной графической модели (вдоль меридиан); М – материал сферы.

В графических системах, основанных на преобладающих в настоящее время принципах объектно-ориентированной теории, данные (О, R, n, m, М) и соответствующая этим данным функция СФЕРА укомплектованы в блок, называемый объектом. Проектируемое изделие может состоять из набора объектов. Данные (О, R, n, m, М) называют в различных графических программах по-разному: атрибутами, свойствами, параметрами. В дальнейшем будем применять термин параметры.

В свою очередь параметры объекта тоже могут быть функциями (объектами). Например, материал (М в формуле (1)) в графических проектных системах представляется в виде объекта, имеющего значительное количество параметров: блеск, прозрачность, плотность и т.д.

В объектно-ориентированной графической системе есть возможность в любой момент времени обратиться к объекту и при необходимости изменить параметры функции. В этом случае функция сохраняется, и если вы меняете параметры функции, объект-примитив, соответствующий этой функции перерисовывается заново с нуля.

В ряде случаев можно изменить тип объекта и соответственно поменять число и тип параметрических данных. Это происходит, когда сферу преобразуют в редактируемую сеть, например, в деталь типа «Рукоятка» сужением нижней части сферы, т.е. перемещением узлов в нижней части сеточной модели бывшей сферы. Функция СФЕРА (О, R, n, m, М) в этом случае перестает быть сферой и преобразуется в функцию СЕТЬ(n; m; ­­x₁,y₁,z₁; … ­­x_n,y_n,z_n; … x_nm,y_nm,z_nm; M), где ­­x₁,y₁,z₁; … ­­x_n,y_n,z_n; … x_nm,y_nm,z_nm – координаты каждой точки сети.

На рис. 2для примерапредставлена сеть с одинаковыми значениями m и n, равными 4. Сеть имеет 16 вершин, со следующими координатами:

Вершина(0,0): 70,260

Вершина(0,1): 70,140

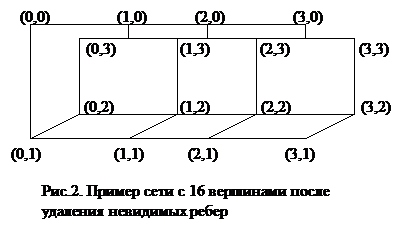Вершина(0,2): 120,165,50

Вершина(0,3): 120,245,50

Вершина(1,0): 170,260

Вершина(1,1): 170,140

Вершина(1,2): 220,165,50

Вершина(1,3): 220,245,50

Вершина(2,0): 250,260

Вершина(2,1): 250,140

Вершина(2,2): 300,165,50

Вершина(2,3): 300,245,50

Вершина(3,0): 350,260

Вершина(3,1): 350,140

Вершина(3,2): 400,165,50

Вершина(3,3): 400,245,50

Дата добавления: 2014-01-05