Статистические методы оценки риска

Основной задачей статистических методов оценки рисков является определение вероятности наступления отдельного неблагоприятного события на основе статистического исследования имеющихся данных о деятельности конкретного рискового объекта (организации) в прошлом.

Наиболее простой формой статистического показателя, характеризующего риск, является показатель размаха вариации ожидаемого результата:

R = X_MAX - X_MIN

где X_MAX, X_MIN – соответственно наибольшее и наименьшее значения результата в выборочном наблюдении.

Достоинством статистического показателя R является простота расчета. Однако размах вариации в этом случае учитывает только крайние значения результата, поэтому область его применения ограничена достаточно однородными совокупностями.

Точнее вариацию результата характеризуют статистические показатели риска, учитывающие значимость колеблемости всех возможных значений результата предпринимательской деятельности. С этой целью частные риски деятельности оцениваются с использованием показателей дисперсии, среднеквадратического отклонения, коэффициента вариации, а результаты их влияния – на основании средних ожидаемых значений исследуемых показателей.

Среднее ожидаемое значение (математическое ожидание) связано с неопределённостью ситуации. Оно выражается в виде средневзвешенной величины всех возможных результатов Е(х) (например, доход), где вероятность каждого результата Р используется в качестве частоты, или веса, соответствующего значения х. В общем виде это можно записать так:

Е _х = А₁Х₁ + А₂Х₂ +... + А_пХ_п =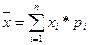

Средняя величина представляет собой обобщённую количественную характеристику и не позволяет принять решение в пользу какого-либо варианта вложения капитала.

Изменчивость (колеблемость) ожидаемого результата – это степень отклонения ожидаемого значения от средней величины. В данном случае риск измеряется: дисперсией, среднеквадратическим отклонением, коэффициентом вариации.

Важной характеристикой, определяющей меру изменчивости возможного результата, является дисперсия (Д) – средневзвешенное квадратов отклонений случайной величины от ее математического ожидания (т.е. отклонений действительных результатов от ожидаемых):

Из последней формулы видно, что дисперсия имеет размерность квадрата случайной величины. Для получения линейной оценки рассеивания случайной величины из дисперсии извлекают корень:

где σ - среднее квадратичное или стандартное отклонение. Оно показывает то, что мы можем потерять.

Данный показатель предупреждает о наличии отклонений, но при этом не показывает конкретного направления, где нас могут ждать потери. Чем больше величина стандартного отклонения, тем больше разброс ожидаемого результата, а, следовательно, тем выше риск анализируемой сделки.

И дисперсия, и среднеквадратическое отклонение являются абсолютными мерами риска и измеряются в тех же физических единицах, в каких изменяется варьирующий признак.

Для анализа меры изменчивости часто используют коэффициент вариации (V), который представляет собой отношение среднеквадратического отклонения к математическому ожиданию:

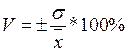
Коэффициент вариации характеризует размер отклонения на единицу ожидаемого результата. Этот показатель используют в тех случаях, когда у разных вариантов ожидается равный результат, но с разными отклонениями. Считается, что чем ниже коэффициент вариации, тем меньше размер относительного риска. Коэффициент вариации – относительная величина. Поэтому с его помощью можно сравнивать колеблемость признаков, выраженных в различных единицах измерения. Диапазон значений вариаций от 0 до 100. Известна шкала изменений различных значений коэффициента вариаций для измерения риска:

Если V до 10% - слабая колеблемость и слабый риск;

10% - 25% - умеренная колеблемость, умеренный риск;

свыше 25% - высокая колеблемость, высокий риск.

Выявление степени тесноты взаимосвязи между переменными (объемом инвестиций и показателями инвестицион­ной привлекательности), основывается на расчете ко­эффициента корреляции.

,

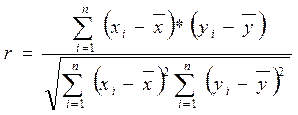где r – показатель, определяющий тесноту связи между факторами и результативным признаком, в качестве которого мы рассматриваем инвестиции в основной капитал. Чем больше значение r, тем больше эта зависимость. Значения показателя могут колебаться от 0 до 1.

х – факторный признак;

у – результативный признак, который определяет факторы, имеющие наиболее тесную связь с результативным показателем.

В мировой практике критические зна­чения коэффициента корреляции 0,5 и - 0,5. Если модуль коэф­фициента корреляции больше 0,5, считается, что между пере­менными сильная взаимосвязь. В противном случае взаимосвязь между переменными - слабая. Если значение коэффициента кор­реляции положительное, взаимосвязь между переменными прямая, т.е. при росте фактора растет и объем инвестиций. Если же значение коэффициента корреляции отрицательная величина, то связь обратная и при росте фактора объем инвестиций падает.

Для определения достоверности рассчитанного коэффициента корреляции используют гипотезу проверки наличия связи между показателями.

СРАВНИТЕЛЬНАЯ ОЦЕНКА ВАРИАНТОВ РЕШЕНИЙ С ПОМОЩЬЮ СТАТИСТИЧЕСКИХ ОЦЕНОК.

На практике для сравнительной характеристики проектов по степени риска особенно в инвестиционно-финансовой сфере, в качестве количественного критерия широко используется, как уже указывалось, среднее ожидаемое значение результата деятельности (доход, прибыль, дивиденды и т.п.), среднее квадратическое отклонение, как мера изменчивости возможного результата, а так же коэффициент вариации.

Если имеются две стратегии А и В, для которых известны Е_А, ЕВ, σ_А и σ_В, то предложение должно быть отдано стратегии А, если:

1.Е_А> Е_В, σ_A = σ_B и V_A < V_B,

2.Е_А > Е_В, σ_А < σ_В и V_А < V_B,

3.Е_А = Е_В, σ_А < σ_В и V_А < V_B.

Предпочтение варианту В следует отдавать при:

4.Е_А < Е_В, σ_А = σ_В и V_А > V_В,

5.Е_А < Е_В, σ_А > σ_В и V_A > V_B,

6.Е_А = Е_В, σ_А> σ_В и V_А> V_B.

В общем случае, когда Е_А > Е_В, σа > σв или Е_А < Е_В, σ_А < σ_В, требуются дополнительные исследованию, как и в нашей ситуации.

Заказчик может выбрать стратегию с большим ожидаемым доходом, связанным, однако, с большим риском, или стратегию с меньшим ожидаемым доходом, но более гарантированным и ме­нее рискованным.

Можно также отдать предпочтение стратегии, которая харак­теризуется меньшим коэффициентом вариации V и, как следствие, обеспечивает более благоприятное соотношение риска (σ) и дохода (Е).

Использование одного из этих двух подходов к выбору опти­мальной стратегии может привести к заметным ошибочным ре­зультатам.

На основе вышеизложенного можно сделать следующие выводы:

1. С помощью статистических показателей оценки риска можно оценить риск не только конкретной сделки, но и предпринимательской фирмы в целом на основе ее доходов за некоторый промежуток времени.

2. Преимущество оценки предпринимательского риска на основе статистических показателей – несложность математических расчетов, а явный недостаток – необходимость добывания большого объема исходных данных (чем больше массив, тем достовернее оценка риска), что не всегда возможно. Поэтому использование статистических показателей ограничено.

3. Дисперсия сигнализирует о наличии риска, но при этом скрывает направление отклонения от ожидаемого значения, т.к. в формуле для определения СКО стоит квадрат разности, а предпринимателю важен знак этого отклонения для того, чтобы знать, что в результате совершения данной сделки наиболее вероятно: потери или прибыль.

4. Важно еще раз подчеркнуть, что хотя дисперсия (СКО) – инструмент достаточно эффективный в качестве меры риска, он не всегда отражает некоторые реалии современной экономической действительности. Возможны ситуации, при которых анализируемые варианты имеют приблизительно одинаковую среднюю прибыль и одинаковые дисперсии, но не являются в равной мере рисковыми. Если под риском понимать риск разорения (банкротства), то величина риска должна зависеть от величины исходного капитала.

5. Еще одной особенностью статистических показателей риска является то, что расчет только уровня риска не всегда позволяет принять однозначное решение в пользу того или иного варианта действий.

3. Использование метода «дерево решений» для оценки риска

Вероятностная постановка задачи выбора оптимальных решений в экономике более адекватно отображает реальные ситуации. Поэтому применение вероятностных моделей во многих случаях позволяет уменьшить риск при выборе наиболее эффективных решений. Однако применение указанных моделей связано с не­обходимостью определения вероятностных характеристик ана­лизируемых процессов (ситуаций). Это существенно усложняет решение рассматриваемых задач. Во многих случаях вероят­ностное распределение экономических показателей бывает не­известным. Поэтому возникает необходимость определения предпочтительных альтернатив при условии, что вероятностные характеристики экономических показателей являются неизвест­ными.

В условиях полной неопределенности, когда вероятности рас­сматриваемых ситуаций неизвестны, можно пользоваться пра­вилом Лапласа, заключающимся в том, что все неизвестные вероятности Pj считают равными. После этого выбор эффектив­ного решения можно принимать или по правилу максимизации среднего ожидаемого выигрыша или по правилу минимизации среднего риска. Подобный критерий принятия ре­шения можно назвать принципом недостаточного обоснования Лапласа.

Специфическим графическим инструментом анализа проблем­ных ситуаций являются, так называемые, деревья решений. Тер­мин получил свое название от древообразующей структуры схемы.

С помощью этого метода решается целый ряд задач, когда имеются два или более последовательных множества решений, причем, последующие решения основываются на результатах пре­дыдущих состояний среды, т.е. появляется цепочка решений, вы­текающих одно из другого. Подобные задачи проще решать с ис­пользованием дерева решений, которое представляет собой гра­фическое изображение последовательности решений и состояний среды с указанием соответствующих вероятностей и выигрышей для всевозможных комбинаций.

Для упрощения применения этого метода разобьем его на не­сколько этапов.

На первом этапе формулируем задачу. Отбрасываем не отно­сящиеся к проблеме факторы, а оставшиеся подразделяем на су­щественные и несущественные. Далее: определяем возможности сбора информации для экспериментирования и реальных дей­ствий; составляем перечень событий, которые с определенной ве­роятностью могут произойти: устанавливаем временной порядок расположения событий, в исходах которых содержится полезная и доступная информация, и тех последовательных действий, ко­торые можно предпринять.

На втором этапе строим дерево решений. Оно состоит из двух основных частей: «решений» и «вероятностных событий». Они представлены квадратами. Эти решения и вероятност­ные события связаны, что видно из последующих примеров.

Суть третьего этапа состоит в оценке вероятностей состояний среды, т.е. сопоставлении шансов возникновения каждого конкретного события.

Установление выигрышей (или проигрышей) для каждой возможной комбинации альтернатив (действий) состояний среды составляют четвертый этап.

На пятом этапе решается задача.

Дерево решений состоит из ряда узлов и исходящих из них ветвей. Квадраты обозначают пункты принятия решений (или возможные события), а дуги соответствуют переходам между логически связанными решениями и случайными событиями. Из вершин — решения (квадратов) исходит столько дуг, сколько имеется вариантов (альтернатив), выбор конкретной дуги (вариант решения) осуществляется ЛПР. Из вершины — события также может исходить несколько дуг. Но здесь уже выбор осуществляется случайным образом в соответствии с заданными вероятностями отдельных исходов.

После того, как дерево решения построено, оно анализируется справа налево, т.е. начинать надо с последнего принятого ре­шения. Для каждого решения выбирается альтернатива с наибольшим показателем отдачи (или с наименьшими затратами). Если за принятием решения следует несколько возможных вариантов событий, то выбирается альтернатива с наибольшей предполагаемой прибылью (или с наименьшей предполагаемой величиной затрат).

Например, рассмотрим задачу максимизации ожидаемой прибыли от акций

Предположим, что мы владеем акциями стоимостью 1000 у.е. Мы должны принять решение относительно того, держать, ли акции, продать их все или купить еще акции на сумму 500 у.е. Вероятность 20%-го роста курсовой стоимости акции составляет 0,6, а вероятность снижения курсовой стоимости на 20% - 0,4. Какое решение необходимо принять с тем, чтобы максимизировать ожидаемую прибыль?

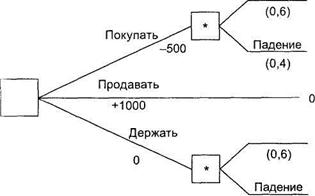
Сначала необходимо решить, что делать с акциями: купить еще, все продать или все держать. Это отображено с помощью дерева решений на рисунке.

Рост курсовой стоимости

1800

Рост курсовой стоимости

Диаграмма содержит величину доходов или расходов в случае принятия того или иного решения. Например, вариант «продажи» даст доход в 1000 у.е. (показан как + 1000 на дереве). В противоположность этому, вариант «покупки» принесет расходы в сумме 500 у.е. (показаны как — 500 на дереве). Если мы продадим акции, тогда их у нас будет ноль.

Если мы просто будем держать акции, то в случае 20%-ного подъема на рынке их стоимость составит 1200 у.е., а в случает 20%-ного спа­да — 800 у.е. В другом случае, после покупки акций еще на 500 у.е., при подъеме рынка мы окажемся обладателями акций стоимос­тью 1800 у.е., а при падении — стоимостью 1200 у.е. Данные зна­чения указаны в конце каждой ветви в правой части дерева реше­ний. Дерево также показывает вероятности возможных событий (т.е. рост или падение курсовой стоимости акций), а также денежные средства, затраченные или полученные при этом, Например, покупка акции стоит 500 у.е. (т.е. в данной точке диаг­раммы указано — 500 у.е.). Аналогично, продажа акций даст до­ход в 1000 у.е., и это указано рядом с соответствующей ветвью дерева.

Начиная с правой стороны и двигаясь влево, производится расчет ожидаемых значений. Таким образом, ожидаемое значение в блоке вероятностных событий А рассчитывается путем умножения каждой вероятности на значение в конце ветви, т.е. ожидаемое значение в блоке А составляет:

0,6 * 1800 + 0,4 * 1200 = 1560 у.е.

Аналогично, ожидаемое значение для блока Б составляет:

0,6 * 1200 + 0,4 * 800 = 1040 у.е.

И наконец, можно принимать решение на основании вывода ожидаемых значений по соответствующим ветвям обратно к блоку решений В. Три возможных пути обратно к блоку В дают следующие значения:

Вариант 1: 1560 - 500 = 1060 у.е.

Вариант 2: 0 + 1000 = 1000 у.е.

Вариант 3: 1040 + 0 = 1040 у.е.

Следовательно, на основании данного критерия с целью максимизации ожидаемой стоимости акций мы предпочтем вариант 1. Таким образом, мы решим купить еще акций на сумму в 500 у.е., что даст нам ожидаемую чистую прибыль в 1060 у.е. Это значение показано в блоке В, а путь решения выделен, как показано на рисунке. Следует отметить, что этот простой способ принятия ре­шений, основанный на максимизации ожидаемой отдачи, может не всегда оказаться приемлемым. Например, также необходимо учитывать факторы риска, о чем мы будем говорить в следующем примере.

Например, выбор оптимального проекта реконструкции фабрики — химчистки

С помощью дерева решений рассмотрим задачу выбора оптимального проекта реконструкции фабрики — химчистки.

Руководство компании решает реконструировать фабрику химчистки по одному из трех проектов. Размер выигрыша, который компания может получить, зависит от благоприятного или неблагоприятного состояния рынка.

Таблица проектов реконструкции

Номер стратегии	Действия компании	Выигрыши, усл. руб., при состоянии экономической среды
благоприятному	неблагоприятному
	По 1-му проекту		- 80000
	По 2-му проекту		- 150000
	По 3-му проекту		- 40000

На основе данной таблицы выигрышей (потерь) построим дерево решений.

Процедура принятия решения заключается в вычислении для каждой вершины дерева (при движении справа налево) ожидаемых денежных оценок, отбрасывании неперспективных ветвей и выборе ветвей, которым соответствует максимальное значение ожидаемой денежной оценки (ОДО). ОДО — это средний выигрыш в игре, которая рассчитывается как сумма произведений размеров выигрышей на вероятности этих выигрышей.

Определяем ОДО:

для 1-й вершины: ОДО1 = 150000 * 0,5 + (-80000) * 0,5 = 35000 усл. руб.;

для 2-й вершины: ОДО₂ = 200000 * 0,5 + (-150000) * 0,5 = 25000 усл. руб.;

для 3-й вершины: ОДО₃ = 100000 * 0,5 + (-40000) * 0,5 = 30000 усл. руб.

Так как истинные вероятности благоприятного и неблагоприятного состояний экономической среды нам неизвестны, то в соответствии с правилом Лапласа равновозможности принимаем наличие состояний с вероятностями 0,5 удачи и 0,5 неудачи.

Из приведенного расчета видим, что наиболее целесообразно выбрать первый проект, а вторую и третью ветви (стратегии) решений можно отбросить. ОДО наилучшего решения равна 35000 усл. руб.

Но на этом исследования не заканчиваются. Руководству ком­пании стало известно, что можно провести дополнительное ис­следование рынка, причем, предоставляемая услуга обойдется компании в 12000 усл. руб. Руководство понимает, что дополни­тельное исследование по-прежнему не способно дать точной ин­формации, но оно поможет уточнить ожидаемые оценки конъюнктуры рынка, изменив тем самым значения вероятностей.

Известно, что фирма, проводящая дополнительные исследо­вания, способна уточнить значения вероятностей благоприятно­го или неблагоприятного исхода. Возможности фирмы в виде ус­ловных вероятностей благоприятности и неблагоприятности рын­ка представлены в таблице.

Прогноз фирмы	Фактически
благоприятный	неблагоприятный
Благоприятный	0,81	0,19
Неблагоприятный	0,23	0,77

Например, когда фирма утверждает, что рынок благоприят­ный, то с вероятностью 0,81 этот прогноз оправдывается (с вероятностью 0,19 могут возникнуть неблагоприятные условия), прогноз о неблагоприятности рынка оправдывается с вероятностью 0,77.

Компания заказала фирме прогноз состояния рынка и фирма утверждает, что ситуация будет благоприятной с вероятностно 0,42 (дерево решений изображено в середине рис) и ситуация будет неблагоприятной с вероятностью 0,58 (дерево решений построено на рис. внизу) При построении дерева решений развитие событий происходит от корня дерева к исходам, а расчет прибыли выполняется от конечных состояний к начальным. Из анализа решения следует, что проведение дополнительных исследований конъюнктуры рынка существенно уточняет принимаемое решение. Если фирма прогнозирует благоприятную ситуацию на рынке, то целесообразно проводить реконструкцию по второму проекту, если прогноз неблагоприятный — по третьему проекту.

При отсутствии точной информации (верхнее дерево ре­шений) максимальная ожидаемая денежная оценка равна ОДО = 35000 усл. руб.

Если точная информация об истинном состоянии рынка будет благоприятной (ОДО = 200000 усл. руб.) принимается второй проект, если неблагоприятной (ОДО = - 40000). Тогда ОДО точной информации равна:

ОДО_Т.И. = 200000 * 0,5 - 40000 * 0,5 = 80000 усл. руб. и ожидаемая ценность точной информации составит:

ОЦ_Т.И. = ОДО_Т.И. - ОДО = 80000 - 35000 = 45000.

Значение ОЦ_Т.И. показывает, какую максимальную цену долж­на быть готова заплатить компания за точную информацию об ис­тинном состоянии рынка в тот момент, когда ей это необходимо.

Дата добавления: 2014-01-05