Обертання навколо ліній рівня

Якщо вісь обертання паралельна якійсь площині проекцій, то це – спосіб обертання навколо ліній рівня. У цьому разі кола обертання проекціюються у відрізки прямих ліній, перпендикулярних до проекції осі обертання на ту площину, якій ця вісь паралельна. Цей спосіб найчастіше вживається для приведення плоскої фігури у положення площини рівня обертанням її навколо горизонталі чи фронталі, що належать цій фігурі. За допомогою цього способу доцільно визначати неспотворені проекції плоских фігур та дійсні величини плоских кутів.

Для приведення плоскої фігури у положення площини рівня достатньо повернути лише одну яку-небудь точку її, оскільки всі точки, що належать осі обертання, залишаються нерухомими. Коли плоска фігура стає паралельною площині проекцій, радіус обертання будь-якої точки її теж стає паралельним тій самій площині проекцій і проекціюється на неї без спотворення – у натуральну величину. Саме на цьому факті ґрунтується побудова проекції повернутої точки.

На вихідному епюрі визначають способом прямокутного трикутника дійсну довжину радіуса обертання точки і відкладають його від центра обертання перпендикулярно до осі обертання. Детальніше суть способу розглянемо на конкретних прикладах.

Нехай задана точка А обертається навколо лінії рівня, наприклад, горизонталі h (рис. 6.14 зліва). Точка А рухається по колу, площина S якого перпендикулярна до горизонталі h і проекціюється на площину П₁ у пряму, що перпендикулярна до проекції h₁ горизонталі h. Центр О кола знаходиться в основі перпендикуляра, якого проведено від точки А до осі h. АО – радіус кола – радіус обертання точки А. Його горизонтальна проекція – А₁О₁.

Коли точка А, обертаючись навколо осі h, суміщується з горизонтальною площиною, що проходить через вісь h (положення Ā), її радіус обертання ОА стає паралельним площині П₁ і проекціюється на неї без спотворення у відрізок О₁Ā₁. Точка А може бути повернута в протилежному напрямі до положення Ā¢. Тоді її горизонтальна проекція буде у точці Ā¢₁.

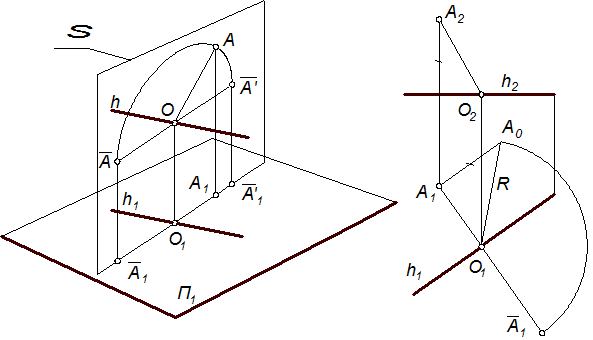На рис. 6.14 справа показано обертання точки А(А₁, А₂) навколо горизонталі h(h₁, h₂) на комплексному кресленні. Радіус обертання ОА(О₁А₁, О₂А₂)

Рис. 6.14

точки А – це перпендикуляр, проведений із точки А на вісь h. Способом прямокутного трикутника визначаємо натуральну величину радіуса обертання R (А₁А₀^А₁О₁, А₁А₀ = Z_A – Z_h) і відкладаємо його від точки О₁ перпендикулярно до h₁. Отримуємо точку Ā₁ – проекцію повернутої точки А.

Обертання навколо ліній рівня доцільно використовувати для визначення неспотворених проекцій (натуральних величин) плоских фігур, відстаней від точки до прямої та між паралельними прямими. За допомогою цього способу можна визначати відстані між мимобіжними прямими та від точки до площини. Але таке застосування способу у навчальній літературі не трапляється. Та найбільш ефективно цей спосіб застосовується для визначення натуральних величин кутів між двома прямими, між прямою і площиною та між двома площинами.

Застосування способу для розв’язування названих задач покажемо на конкретних прикладах.

Приклад 6.1. Визначити неспотворену проекцію трикутника АВС (рис. 6.15)

У площині трикутника АВС через вершину В(В₁, В₂) проводимо горизонталь h(h₁, h₂). Трикутник обертаємо навколо горизонталі h до положення, коли він стане горизонтальним. Точки В і 1(1₁, 1₂) (1ÎАС) залишаються нерухомими. Отже, достатньо повернути лише точку А(А₁, А₂). Способом прямокутного трикутника визначаємо дійсну довжину О₁А₀ радіуса обертання (А₁А₀^О₁А₁, А₁А₀ = Z_A – Z_h) і відкладаємо його від точки О перпендикулярно до проекції h₁ горизонталі h. Маємо горизонтальну проекцію Ā₁ оберненої точки Ā. Сполучаємо точку Ā₁ з нерухомими точками В₁ та 1₁. Вершина С(С₁, С₂) під час обертання трикутника обертається по своєму колу, дуга якого зобразилась у відрізок С₁₁ ^ h₁. Сполучивши точку ₁ з точкою В₁, дістаємо неспотворену проекцію Ā₁В₁₁ трикутника АВС.

Рис. 6.15 Рис. 6.16

Приклад 6.2. Визначити дійсну величину відстані від точки К до прямої l (рис. 6.16).

У площині Г(К; l) проводимо фронтальf(f₁, f₂) через точку К(К₁, К₂) і обертаємо навколо цієї фронталі пряму l (l₁, l₂), точніше, будь-яку точку її, наприклад, точку D(D₁, D₂). Для цього способом прямокутного трикутника визначаємо дійсну величину О₂D₀ радіуса OD(O₂D₂) обертання точки D (D₂D₀ ^ O₂D₂, D₂D₀ = Y_f – Y_D) і відкладаємо його від точки О₂ перпендикулярно до f₂, дістаємо фронтальну проекцію 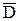₂ повернутої точки 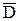. Сполучаємо точку 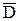₂ з проекцією 1₂ нерухомої точки 1 прямої l. Маємо фронтальну проекцію ₂ повернутої прямої l. Перпендикуляр, проведений із точки К₂ на пряму ₂ визначає дійсну величину відстані від точки К до прямої l.

Приклад 6.3. Визначити дійсну величину кута між прямими a i b (рис.6.17).

У площині Δ (a; b) проводимо фронталь f(f₁, f₂) і обертаємо навколо неї площину Δ до фронтального положення. Для цього достатньо повернути лише точку А(А₁, А₂) перетину прямих a i b, оскільки точки 1(1₁, 1₂) і 2(2₁, 2₂), через які проходить вісь обертання f, нерухомі.

Проекція Ā₂ побудована аналогічно тому, як побудована точка ₂ на рис. 6.16 (А₂А₀^О₂А₂, Ā₂О₂ = О₂А₀). Точку Ā₂ сполучаємо з точками 1₂ і 2₂.

Відрізки Ā₂1₂ і Ā₂2₂ - це фронтальні проекції відрізків повернутих прямих a i b. Кут a = ā₂;^ 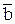- це дійсна величина кута між прямими a i b.

Визначення натуральних величин кутів між мимобіжними прямими, між прямою і площиною, а також між двома площинами може бути зведено до визначення кута між двома прямими, що перетинаються. Приклад 6.4. Визначити дійсну величину кута між мимобіжними прямими m(m₁, m₂) і n(n₁, n₂) (рис. 6.18).

Мірою кута між мимобіжними прямими є кут між прямими, що перетинаються і паралельні даним мимобіжним. Тому через будь-яку точку, наприклад, К(К₁, К₂) прямої n проводимо пряму с (с₁, с₂) паралельну прямій m і визначаємо дійсну величину кута між прямими n i c, як це зроблено на рис. 6.17.

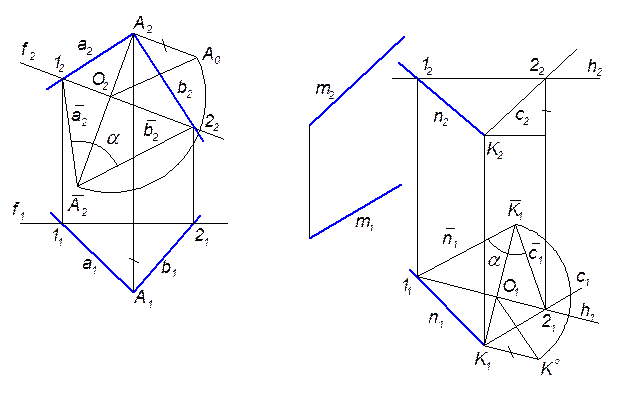Для цього у площині 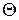(n; с) проводимо горизонталь h(h₁, h₂) і обер

Рис. 6.17 Рис. 6.18

таємо точку К навколо неї так, щоб площина 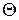стала горизонтальною:

К₁К⁰ = Z_h – Z_k, K₁K⁰ ^ O₁K₁, O₁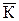₁ =O₁K⁰. Точку 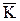₁ сполучаємо з нерухомими точками 1(1₁) і 2(2₁). Кут 1₁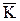₁2₁ становить дійсну величину кута між прямими m і n.

Приклад 6.5. Визначити дійсну величину кута між прямою l(l₁, l₂) і площиною (a; b) (рис. 6.19).

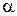Кут між прямою l і площиною вимірюється кутом між цією прямою і її ортогональною проекцією l_G на дану площину (рис. 9.6 зліва). Але кут між прямою і площиною у загальному випадку доцільно визначати за допомогою кута між прямою l і перпендикуляром АА_G до даної площини, який у сумі із шуканим становить 90°.

Тому через будь-яку точку, наприклад, С(С₁, С₂) прямої l проводимо перпендикуляр n(n₁, n₂) до площини (n₁ ^ h ₁, n₂ ^ f₂) (h Ì , f Ì ) і визначаємо дійсну величину кута між прямою l і перпендикуляром n обертанням його навколо горизонталі h^¢(h^¢₁, h^¢₂) як це виконувалось у попередніх прикладах. Кут між відрізками 4₁₁ і 5₁₁ становить дійсну величину кута між прямою l і перпендикуляром n. Доповнимо цей кут до 90°, тобто через точку ₁ проведемо пряму, перпендикулярну до сторони 5₁₁ кута . Кут 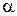між проведеною прямою і відрізком 4₁₁ становить кут між прямою l і площиною .

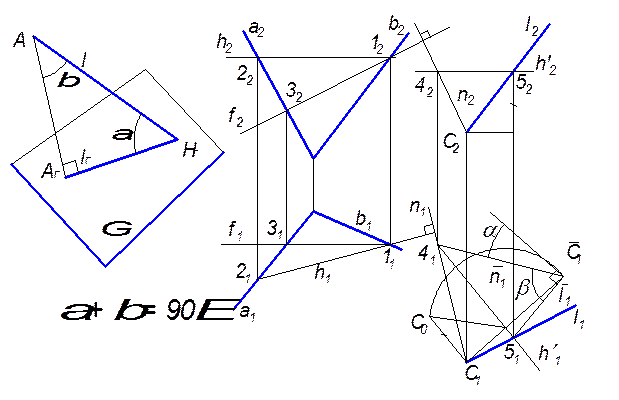Рис. 6.19

Приклад 6.6. Визначити дійсну величину кута між двома площинами

(m|| n) і (h; f) (рис. 6.20).

Рис. 6.20

Двогранний кут між двома площинами вимірюється лінійним кутом між двома прямими лініями перетину заданих площин з третьою площиною, перпендикулярною до заданих. Але визначати величину кута між площинами за такою схемою досить складно. Значно простіше його можна визначити за допомогою кута між двома перпендикулярами, проведеними до даних площин із будь-якої точки простору.

Із довільної точки D(D₁, D₂) простору проводимо два перпендикуляри до заданих площин: l ^(m || n) і k ^(h; f) (l ₁ ^ p₁, l ₂ ^ q₂; k₁ ^ h₁, k₂ ^ f₂). А

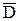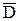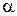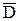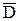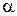далі визначаємо дійсну величину кута між перпендикулярами k і l, обернувши їх навколо горизонталі 45(4₁5₁, 4₂5₂) до горизонтального положення. Точка ₁ – це горизонтальна проекція повернутої точки D. Сполучаємо точку ₁ з нерухомими точками 4₁, 5₁. Кут між відрізками 4₁₁ і 5₁₁ становить кут між площинами і . Якщо доповнити кут до 180°, то

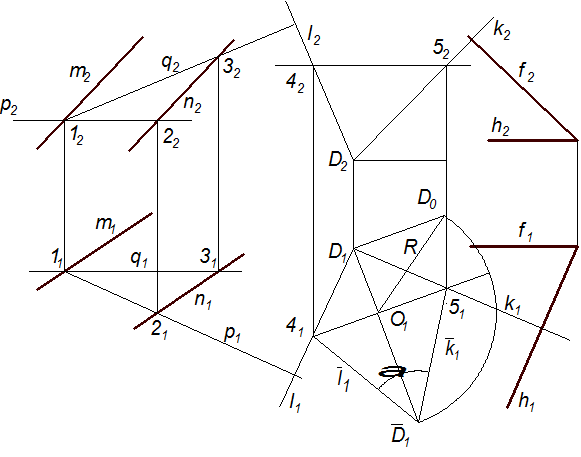отримаємо другий кут між площинами. У даному випадку він тупий. Тому слід прийняти за кут між площинами гострий кут .

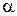6.5.1 Спосіб обертання навколо слідів площини (суміщення)

Плоскі фігури можна обертати навколо слідів (як нульових ліній рівня) площини, котрій належать ці фігури, наприклад, для визначення дійсних величин кутів між прямими або для побудови неспотворених зображень плоских фігур. У цьому разі плоска фігура обертається навколо сліду площини, якій належить задана фігура, до суміщення її з якоюсь площиною проекцій. Площина вважається суміщеною з площиною проекцій, якщо побудовано суміщений з цією площиною слід заданої площини. В літературі таке обертання дістало назву суміщення. Розглянемо декілька прикладів.

На рис. 6.21 показано суміщення площини Г(f⁰, h⁰) з горизонтальною площиною проекцій обертанням її навколо горизонтального сліду h⁰. На фронтальному сліді взято точку 1(1₁, 1₂) і обертанням навколо сліду h⁰(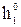) побудовано її суміщене положення 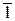₁. Для цього за допомогою прямокутного трикутника О₁1₁1⁰ визначено дійсну довжину О₁1⁰ радіуса обертання точки 1 і за допомогою циркуля відкладено його на перпендикулярі 1₁О₁ до сліду 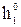. Маємо точку 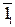. Цю точку можна побудувати інакше. Через точку 1₁ провести перпендикуляр до сліду 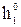і на ньому зробити засічку радіусом Г_х1₂ із центра Г_х. Через точки Г_х і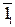проведено суміщений з площиною П₁ фронтальний слід 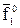. На рис. 6.21 показаний кут α – це дійсна величина кута між слідами f⁰ i h⁰ площини Г.

На рис. 6.22 показано визначення дійсної величини кута між слідами площини Δ(f⁰, h⁰). Цей приклад відрізняється від попереднього лише тим, що кут між слідами площини Δ тупий. Обернемо площину Δ навколо фронтального сліду f⁰(f) до суміщення з фронтальною площиною проекцій П₂ Для цього на сліді h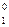(h, h) візьмімо довільну точку 1(1₁, 1₂) і обернемо її навколо сліду f⁰(f) до суміщення з площиною П₂. Відрізок Г_х1₁ – Рис. 6.21

це неспотворена проекція відрізка Г_х1(Г_х1₁ = Г_х1).

У суміщеному положенні цей відрізок не змінює своєї довжини (Г_х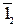= Г_х1). Проекція 1₂ точки 1 переміщується перпендикулярно до f⁰(f). Тому із точки Г_х як із центра проводимо дугу кола радіусом Г_х1₁ до перетину з перпендикуляром 1₂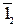до сліду f⁰. Як видно із рис. 6.22 дуга може бути проведеною за годинниковою стрілкою чи проти неї. Отже суміщених положень сліду h⁰ може бути два (на рис. 6.22 показано суцільною тонкою і штриховою). Кут між fі 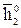і є дійсною величиною кута між слідами площини Г.

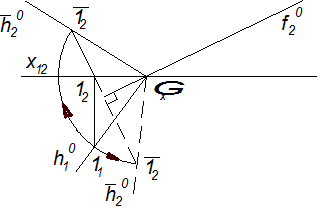Лінії рівня площини, поданої своїми слідами, у суміщеному положенні залишаються паралельними відповідним слідам площини. На рис. 6.23 показано суміщення площини Δ(f⁰, h⁰) з фронтальною площиною проекцій П₂. Суміщений слід 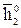побудований за допомогою точки 1(1₁, 1₂), взятої на сліді h⁰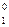(h, h), як це було побудовано на Рис. 6.22

рис. 6.21, 6.22. Через точку 1Îh⁰

у площині Δ проведена фронталь f(f₁, f₂), а через точку 2Îf⁰(2₁Îf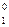, 2₂Îf) – горизонталь h(h₁, h₂).

У суміщеному положенні площини через точку 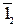проведено суміщене положення 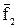фронталі паралельно фронтальному сліду f⁰ площини Δ(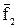êêf₂), а через точку 2₂ – суміщене положення 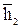горизонталі паралельно суміщеному положенню 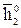горизонтального сліду площини Δ (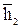êê).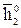

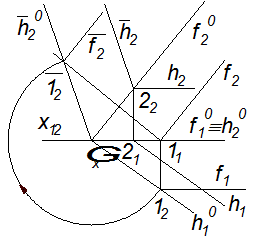Слід ще раз звернути увагу на те, що спосіб суміщення є лише різновидом обертання навколо ліній рівня. Різниця полягає лише в тому, що у суміщенні використовуються площини, подані слідами, тобто нульовими лініями рівня, для яких завжди збігаються горизонтальна проекція фронталі з фронтальною проекцією горизонталі.

Наведемо приклад розв’язання, певним чином, зворотної задачі, в якій за заданим неспотвореним зображенням Рис. 6.23

Δтрикутника ABC, що належить

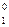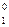площині Q(f⁰, h⁰), необхідно побудувати його горизонтальну та фронтальну проекції. Отже, задано зображення Δтрикутника і сліди f⁰(f, f) та h⁰(h, h) площини. Спочатку будуємо суміщене з площиною П₁ зображення 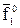фронтального сліду заданої площини. 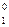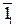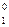Для цього на сліді f⁰ беремо точку 1(1₁, 1₂) (1₁Î f, 1₂Îf) і обертаємо її навколо горизонталі h⁰ до суміщення з площиною П₁, як це було виконано у попередніх прикладах: 1₁^h, Г_х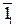= Г_х1₂. Далі зворотним обертанням навколо горизонталі h⁰(h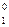), будуємо горизонтальну проекціюА₁ вершини А заданого трикутника. Через вершину суміщеного трикутника проводимо допоміжну горизонталь 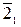площини Q (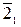êê h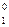). Через точку 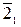проводимо відрізок прямої, перпендикулярної до h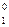, до перетину з проекцією f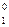(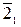2₁ ^ h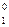), а потім за лінією зв’язку знаходимо фронтальну проекцію 2₂ точки 2 і через проекції 2₁ і 2₂ проводимо відповідно горизонтальну і фронтальну проекції допоміжної горизонталі, якій належить вершина А заданого трикутника. За лініями зв’язку будуємо проекції А₁ і А₂ вершини А: A₁ ^ h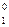, A₁A₂ ^ x₁₂.

Cторони і

трикутника продовжуємо Рис. 6.24

до перетину з горизонтальним

слідом h⁰ площини Q. Маємо точки 3(3₁) і 4(4₁). Під час зворотного обертання площини ці точки залишаються нерухомими. За лініями зв’язку знаходимо їхні фронтальні проекції 3₂ і 4₂ (3₂Îh, 4₂Îh). Проекції А₁ і А₂ вершини А сполучаємо відповідно з проекціями 3₁, 4₁ та 3₂, 4₂. Потім за лініями зв’язку будуємо проекції B₁, B₂ та C₁, C₂ вершин В і С: В₁ÎА₁3₁, В₂ÎА₂3₂; С₁ÎА₁4₁, С₂ÎА₂4₂.

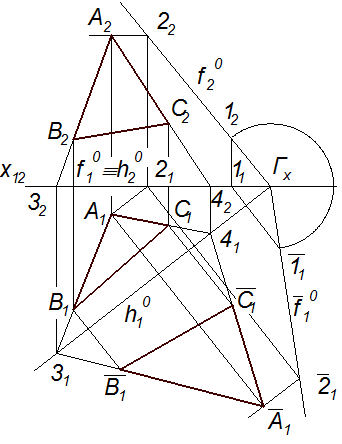Як видно з рис. 6.24, варіантів побудов проекцій А₁, А₂, В₁, В₂, С₁, С₂ вершин трикутника АВС може бути декілька як за послідовністю цих побудов, так і за допоміжними прямими, які використовуються для побудов, тобто кожна з вершин ΔАВС може бути побудована за допомогою горизонталі, фронталі чи будь-якої прямої загального положення площини Q.

Дата добавления: 2014-01-05