Тема 8

А б

А б

А б

А б

А б

А б

А б

А б

А б

А б

А б

А б в

А б

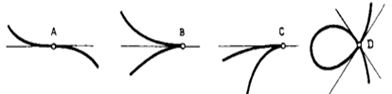
Рисунок 63 – Особые точки кривой

Свойства точек кривой. Точка кри­вой, в которой можно провести единст­венную касательную, называется глад­кой. Кривая, состоящая только из одних гладких точек, называется гладкой кривой. Точка кривой называется обык­новенной, если при движении точки по кривой направление ее движения и на­правление поворота касательной не из­меняются. Точки, не отвечающие этим требованиям, называются особыми.

На рис. 636 изображены особые точки кривой: точка перегиба А — касатель­ная пересекает кривую; точка возврата первого рода В; точка возврата второ­го рода С; точка излома D — кривая в этой точке имеет две касательные.

Проекции плоских кривых. Важное прикладное значение имеют некоторые кривые второго порядка — эллипс, па­рабола, гипербола.

Эллипс (замкнутая кривая с двумя осями симметрии и центром) представ­ляет собой геометрическое место точек, сумма расстояний от каждой из которых до двух данных точек (фокусов) есть величина постоянная (рис. 64 а). Эл­липс можно построить по точкам исходя из его определения. Из точки С радиу­сом а проводят дугу, которая пересека­ет большую ось эллипса в точках F₁ и F₂ — фокусах. Затем из фокусов проводят дуги окружностей радиусами r и 2а — r. Точки пересечения дуг принадлежат кривой эллипса.

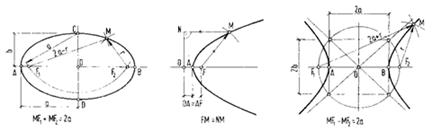
Рисунок 64 – Плоские кривые: а – эллипс, б – парабола, в – гипербола

Построение эллипса помимо спосо­ба, показанного на рис. 64а, в вузах рекомендуют выполнять по восьми точкам: четыре точки — концы сопряженных диаметров и четы­ре точки — пересечения кри­вой эллипса с диагоналями параллелог­рамма.

Парабола (незамкнутая кривая с од­ной осью симметрии) представляет со­бой геометрическое место точек, равно­удаленных от заданной точки (фокуса) и прямой (рис. 64б). Параболу можно построить по точкам исходя из ее опре­деления, если заданы фокус F и прямая ON — директриса. Вершина А парабо­лы делит пополам расстояние между фокусом и директрисой.

Гипербола (кривая, состоящая из двух ветвей, с двумя осями симметрии и центром) представляет собой геомет­рическое место точек, разность рассто­яний от которых до двух данных точек (фокусов) есть величина постоянная (рис. 64в). Две прямые линии, проходя­щие через центр О и касающиеся гипер­болы в бесконечно удаленных точках, называют асимптотами гиперболы. Асимптоты направлены по диагоналям прямоугольника со сторонами 2а и 2b. Гиперболу, как и параболу, можно по­строить по точкам.

Окружность — самая распростра­ненная кривая, при параллельном про­ецировании она преобразуется в эллипс.

Пространственные кривые. Пространственные кривые ли­нии могут иметь самую разнообразную форму. Они могут быть заданы анали­тически. Кривые случайного вида зада­ются графически. Для анализа про­странственной кривой необходимо уста­новить самые общие ее свойства, кото­рые изучаются по ее проекциям.

Для задания на чертеже пространственной кривой линии и точек, принадлежащих ей, достаточно двух ее проекций — горизонтальной и фронтальной. Однако более глубокие ло­кальные свойства пространственной кривой в окрестности любой ее точки исследуются с помощью проекций на гра­нях так называемого сопровождающего трехгранника, который неизменно свя­зан с движущейся по кривой точкой.

Проекции пространственных кри­вых. Наибольшее применение в практи­ке архитектурного проектирования и в технических формах имеют закономерные пространствен­ные кривые, в частности винтовые ли­нии (цилиндрические и конические). Винтовая линия образуется двой­ным движением точки — поступатель­ным и вращательным.

Цилиндрическая винтовая линия — это путь точки, равномерно движущейся вдоль образую­щей цилиндра, которая, в свою очередь, с по­стоянной угловой скоростью перемещается вок­руг оси цилиндра (рис. 65).

Фронталь­ная проекция цилиндрической винто­вой линии представляет собой синусои­ду, гори­зонтальной — окружность. Смещение точки вдоль образующей за один оборот называется шагом h вин­товой линии. При развертывании цилин­дрической поверхности в плоскость ци­линдрическая винтовая линия изобра­зится прямой линией. Угол ψ, составлен­ный касательной к винтовой линии с пло­скостью, перпендикулярной оси, называ­ется углом подъема винтовой линии.

Видимая часть винтовой линии имеет подъем в правую строну (подъем винтовой линии осу­ществляется против часовой стрелки) — это правая винтовая линия, если же наоборот — левая.

Путь, пройденный точкой за один оборот об­разующей вокруг оси цилиндра, называется витком винтовой линии. Кроме этого, цилин­дрическая винтовая линия характеризуется еще ходом, шагом и углом подъема.

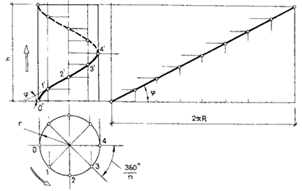
Рисунок 65 -Построение проекций цилиндрической винтовой линии

Винтовые линии могут быть одноходовыми и многоходовыми. Чтобы получить многоходо­вую винтовую линию, надо заданный ход ее разделить на соответствующее число равных частей и от точек деления построить на цилин­дре винтовые линии того же хода.

Для того чтобы получить проекцию кривой линии, надо спроецировать на плоскость проекций ряд принадлежащих ей точек, а для определения длины какого-либо участка ее надо вписать в эту кривую ломаную линию и определить длину каждого ее звена. На рис. 65 справа представлена развертка цилиндрической винтовой линии.

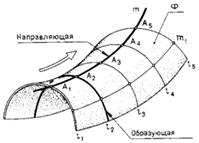
Кривые поверхности. В начертательной геометрии по­верхность рассматривается как непрерывное множество последовательных положений линии, перемещающей­ся в пространстве по определенному закону (рис. 66). Такой способ образова­ния поверхностей называюткинемати­ческим.

Если направляющей является линия, подчи­ненная какому-либо закону, полученная при этом поверхность будет закономерной, в про­тивном случае — случайной.

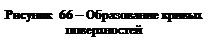Линию l, которая при своем движении образует поверхность, называют образующей. Образующая может пере­мещаться по какой-либо другой неподвижной линии т, называемой направ­ляющей. Поскольку образующая и на­правляющая могут иметь самую различную форму, то и поверхностей мо­жет быть образовано бесчисленное множество. Вместе с тем форма и закон перемещения образующей единствен­ным образом определяют вид кривой поверхности.

Определитель и каркас поверхности. При движении образующей каждая ее точка описывает в пространстве не­которую линию т₁. Таким образом, вся поверхность окажется покрытой сетью линий, состоящей из двух семейств: семейства образующих l₁, l ₂,... и семейства линий т, т₁ …., описываемых отдель­ными точками образующей. Каждая ли­ния одного семейства пересекает все линии второго семейства. Для изобра­жения на чертеже выделяют некоторое количество линий, которые образуют линейный каркас поверхности.

Если закон движения образующей и ее форма определенным образом зада­ны, то поверхность в начертательной геометрии определяют не каркасом, а образующей и условиями ее перемеще­ния. При этом чертеж поверхности дол­жен быть таким, чтобы на нем можно было выделить и построить любую ли­нию и точку, принадлежащие поверх­ности.

Совокупность геометрических эле­ментов и условий, необходимых и до­статочных для однозначного задания поверхности в пространстве и на черте­же, называют определителем кинема­тической поверхности.

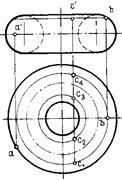
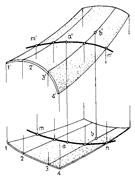
Рисунок 67 – Построение точки, принадлежащей поверхности

Из сказанного выше можно сделать следующий вывод: поверхность счита­ется заданной, если относительно лю­бой точкипространства однозначно решается вопрос о принадлежности ее к данной поверхности.

Точка принадлежит по­верхности, если она лежит на линии этой поверхности.

Чтобы по одной проекции точки, принадлежащей поверхности, постро­ить вторую ее проекцию (рис. 67а), необходимо построить каркас поверх­ности I — II — III — IV, провести че­рез заданную проекцию точки, например, а', вспомогательную линию т' — п', принадлежащую поверхно­сти, а затем построить вторую проек­цию вспомогательной линии т — п и проекцию искомой точки а. Если обра­зующая каркаса совпадает с заданной проекцией точки b, построение второй проекции упрощается.

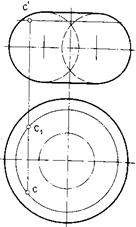
Чтобы построить горизонтальную проекцию произвольной точки С (рис. 67б), принадлежащей поверхности вращения, необходимо провести через фронтальную проекцию с' вспомога­тельную параллель поверхности. За­тем, построив горизонтальную проек­цию параллели (окружность), опреде­лить на ней горизонтальную проекцию точки с. Как следует из приведенного построения, фронтальной проекции точки с' на горизонтальной проекции может соответствовать любая из четы­рех проекций точек с₁ и с₄, лежащих на параллели внешней части поверхности, или с₂ и с₃, лежащих на параллели внут­ренней части поверхности. Точка А ле­жит на экваторе поверхности, точка В — на главном меридиане.

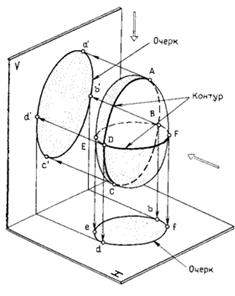Чтобы при­дать чертежу поверхности наглядность, строят ее очертание — проекцию ли­нии контура поверхности (рис. 68).

Контуром или контуром видимости поверхности называется линия, точки которой являются точками каса­ния проецирующих прямых. Проекция контура на плоскости проекций назы­вается очертанием или очерком повер­хности на данной плоскости (рис. 68). При изображении поверхности на чер­теже проекцию контурной линии назы­вают линией видимости, которая явля­ется границей, отделяющей видимую часть поверхности от скрытой, невиди­мой части на данной плоскости проек­ций.

Классификация поверхностей. Из большого числа возможных способов образования поверх­ностей рассмотрим основные способы, выделив главные признаки их класси­фикации.

1. По закону движения образующей — поверхности с поступательным, с вращательным и винтовым движением образующей.

2. По виду образующей различают поверхности с прямолинейной образу­ющей — линейчатые и с криволинейной — нели­нейчатые.

3. По закону изменения формы оразующей — с образующей постоянно­го или переменного вида.

4. По признаку развертывания по­верхности на плоскость — развертыва­емые и неразвертываемые.

5. По способу задания поверхно­сти — аналитическому или графическо­му.

6. По дифференциальным свойст­вам — гладкие или негладкие поверх­ности и по признаку кривизныповерх­ности.

Необходимо отметить, что одни и те же поверхности могут быть классифи­цированы по различным признакам. Поэтому в качестве основного призна­ка выделим вид образующей и характер ее перемещения, т. е. кинематический признак образования поверхностей.

Закон перемещения удобно зада­вать неподвижными линиями — на­правляющими, которые должны пере­секать движущаяся образующая.

Классификация кривых поверхностей представлена на схеме 1 и далее более подробно будут рассмотрены подклассы линейчатых и нелинейчатых поверхностей.

По виду образующей поверхности могут быть подразделены на две большие группы: линей­чатые — образующей является прямая линия и нелинейчатые — образующей является кри­вая линия.

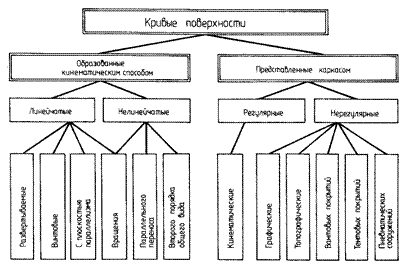Схема 1 – Классификация кривых поверхностей

Линейчатые поверхности в свою очередь де­лятся на развертывающиеся, т. е. такие, кото­рые могут быть совмещены с плоскостью, не претерпев при этом никаких повреждений (складок, разрывов), и неразвертывающиеся (косые).

Наиболее распространенными из линейчатых развертывающихся поверхностей являются ци­линдрическая и коническая.

Цилиндрическая поверхность (рис. 69а) — этоповерхность, образуемая прямой линией (образующей АВ), перемещающейся в прост­ранстве по некоторой неподвижной кривой (на­правляющей MN), оставаясь параллельной за­данному направлению S.

Цилиндрическая поверхность на эпюре мо­жет быть определена проекциями одной из об­разующих и направляющей, так как этого вполне достаточно, чтобы построить на этой по­верхности любую образующую или любую точ­ку (рис. 69б).

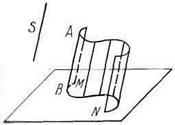
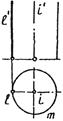
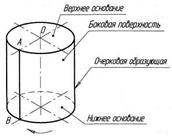
Рисунок 69 – Цилиндрическая поверхность

Если в сечении цилиндрической поверхности плоскостью, перпендикулярной к ее образующим (в нормальном сечении), получается круг, цилиндрическая поверхность называется кру­говой (рис. 69б), если эллипс, — эллиптической, если па­рабола,— параболической и т. д. На рис. 69а изображена цилиндрическая поверхность общего вида — нормальным сечением ее явля­ется кривая неопределенного вида.

Часть цилиндрической поверхности, ограни­ченная двумя плоскими параллельными сече­ниями, называется цилиндром. Если основани­ем цилиндра является его нормальное сечение, цилиндр прямой, если какое-либо наклонное — наклонный.

Коническая поверхность (рис. 70а) — это по­верхность, образуемая движением прямой ли­нии (SA) по некоторой кривой (MN) и прохо­дящей во всех своих положениях через непод­вижную точку (S), называемую вершиной ко­нической поверхности.

Часть конической поверхности, ограниченная вершиной и плоскостью, пересекающей все ее образующие, называется конусом. Если осно­ванием конуса является нормальное сечение, конус прямой, во всех остальных случаях — наклонный.

На эпюре коническая поверхность полностью будет определена проекциями одной направля­ющей и вершины (рис. 70б).

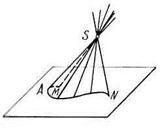
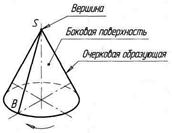
Рисунок 70 – Коническая поверхность

К числу линейчатых развертывающихся по­верхностей относятся также поверхности с реб­ром возврата. Они образуются перемещением прямой линии по некоторой пространственной кривой, причем образующая прямая остается все время касательной к направляющей (рис.71а). При продлении касательных в про­тивоположную сторону от точек касания (точек 1, 2, 3, 4, 5) будет образована вторая полость поверхности. Границей же между первой и вто­рой полостями будет являться направляющая кривая MN, называемая ребром возврата. Эпюр некоторой поверхности с ребром возвра­та приведен на рис. 71б.

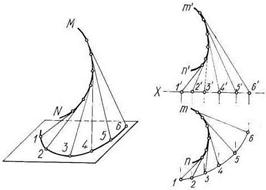
Рисунок 71 – Поверхность с ребром возврата

Из линейчатых неразвертывающихся повер­хностей следует в первую очередь отметить ци­линдроиды - поверхности с плоскостью параллелизма, т. к. поверхности, образуемые движе­нием прямой, скользящей по двум кривым на­правляющим, не лежащим в одной плоскости, и остающейся все время параллельной некоторой заданной плоскости (Р), называемой пло­скостью параллелизма (рис. 72а). Эпюр цилин­дроида приведен на рис. 72б.

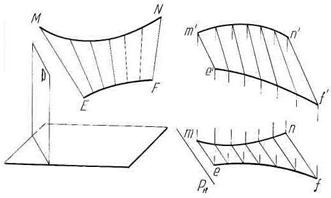
Рисунок 72 – Цилиндроид: а – модель, б – эпюр

Если одной из направляющих цилиндроида является прямая линия, образуется новая ли­нейчатая неразвертывающаяся поверхность с плоскостью параллелизма, называемая коноидом (рис. 73).

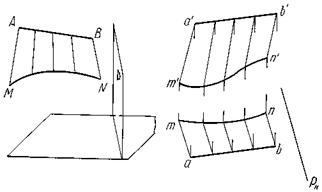
Рисунок 73 -Коноид: а – модель, б – эпюр

Если же обе направляющие цилиндроида за­менить прямыми линиями (скрещивающими­ся), то образуется линейчатая неразвертываю­щаяся поверхность с плоскостью параллелизма — косая плоскость, или ли­нейчатый параболоид, или гиперболический па­раболоид (рис. 74).

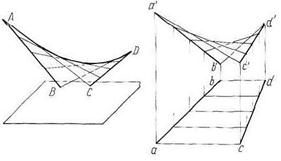
Рисунок 74 -Косая плоскость, или ли­нейчатый параболоид, или гиперболический па­раболоид: а – модель, б – эпюр

Большую группу линейчатых неразвертывающихся поверхностей составляют винтовые по­верхности (гелисоиды или геликоиды), имеющие широкое применение в технике. Винтовые поверхно­сти — это такие поверхности, у которых хотя бы одна направляющая — винтовая линия (рис. 60).

Если прямая линия (образующая) переме­щается в пространстве, пересекая винтовую ли­нию и ее ось (направляющие), то винтовую поверхность называют гелисоидом. Если угол между прямой линией и осью винтовой линии остается по­стоянным и неравным 90°, образуется поверхность, называемая косым (или наклонным) гелисоидом (рис. 70).

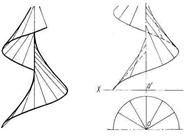
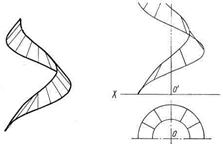
Рисунок 70 – а -косой гелисоид, б -косой кольцевой гелисоид

В этом случае, когда угол между образую­щей косого гелисоида и осью винтовой линии постоянен и равен 90°, получается прямой гелисоид, или винтовой коноид.

На рис.70б показана поверхность, называе­мая косым кольцевым гелисоидом. Она обра­зуется прямой линией, которая, перемещаясь в пространстве, пересекает две соосные винто­вые линии одинакового шага. Причем угол между образующей и осью винтовых линий должен быть постоянным и не равным 90°.

Если же этот угол постоянен и не равен 90°, поверхность называется винтовым цилиндрои­дом.

К нелинейчатым относится также большая группа поверхностей, которые могут быть полу­чены вращением некоторой кривой линии вокруг неподвижной прямой — оси поверхности, т. е. поверхностей вращения. К поверхностям вращения могут быть отнесены также рассмотренные ранее прямой круговой цилиндр и прямой круговой конус. Но это поверхности вращения с прямолинейными образующими, т. е. линейчатые по­верхности вращения.

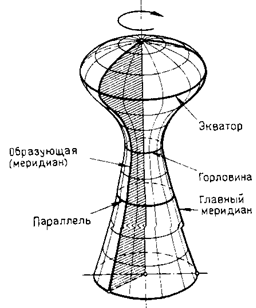При образовании поверхностей вращения каждая точка их образующих перемещается по окружности, перпендикулярной к оси враще­ния (рис.71). Эти окружности называются параллелями, а наибольшая из них — экватором. Осевая пло­скость называется меридиональной, а линия ее пересечения с поверхностью — меридианом.

Вид поверхности вращения зависит от формы образующей и ее положения относительно оси вращения. Рассмот­рим поверхности вращения, образован­ные вращением кривой линии.

Сферическая поверхность (шар) — это по­верхность, образуемая вращением окружности вокруг ее диаметра

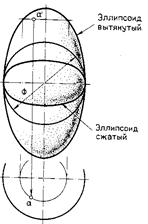
Эллипсоид вращения — это поверхность, об­разуемая вращением эллипса вокруг его боль­шой (вытянутый эллипсоид вращения) или ма­лой (сжатый эллипсоид вращения) оси (рис.72а).

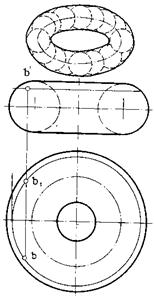
Тор (круговое кольцо) — поверхность, обра­зуемая вращением окружности вокруг оси, лежащей с ней в одной плоскости и ее не пересе­кающей (рис.72б, в). Если окружность не пересекает ось вращения, поверхность называют открытым тором, или кольцом. Если ось касается окружности, то поверхность называют закрытым тором, а ес­ли ось пересекает окружность, тор на­зывают самопересекающимся.

а б в

Рисунок 72 – а – эллипсоид вращения, б – открытый тор, в – закрытый тор

В общем виде торовая поверхность — это поверх­ность, образуемая вращением окружности (или ее дуги) вокруг оси, расположенной с нею в одной плоскости, но не проходящей через ее центр.

Параболоид вращения (рис. 73) — по­верхность, образуемая вращением параболы вокруг ее оси (меридиан поверхности – парабола).

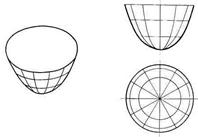
Рисунок 73 – Параболоид вращения: а – модель, б – эпюр

Двуполостной гиперболоид вращения (рис.74) — поверхность, образуемая вра­щением гиперболы вокруг ее действительной оси.

Рисунок 74 – а -двуполостной гиперболоид вращения, б -однополостной гиперболоид вращения

Однополостной гиперболоид вращения (рис. 74б) — поверхность, образуемая вра­щением гиперболы вокруг ее мнимой оси.

Поверхностью второго порядка об­щего вида называют поверхность, ко­торую можно выразить алгебраиче­ским уравнением второй степени в пространственной системе коорди­нат. К поверхностям второго порядка общего вида относятся: трехосный эл­липсоид, однополостный и двуполостный эллиптические гиперболоиды, ги­перболический параболоид.

Касательная плоскость, нормаль, кривизна поверхности. Построение касатель­ной плоскости к поверхности представ­ляет частный случай пересечения по­верхности плоскостью.

Касательной плоскостью к поверх­ности в данной точке называют пло­скость, содержащую множество пря­молинейных касательных, проведен­ных к кривым, проходящим через дан­ную точку. Плоскость может касаться поверхности в точке, если поверхность выпуклая (рис.75а), и по прямой линии, если поверхность линейчатая развер­тываемая, например цилиндр или конус вращения. Плоскость, касаясь вогнутой поверхности в точке, может одновре­менно пересекать ее, например поверх­ность однополостного гиперболоида вращения (рис.75б). Если в какой-либо точке поверхно­сти можно провести касательную плоскость, точка называется обыкновен­ной, а если несколько касательных пло­скостей, точка называется особой.

Понятие о кривизне поверхности. При исследовании свойств поверхно­сти, связанных с ее формой, касатель­ная плоскость играет важную роль.

Касательная плоскость Р к поверх­ности Ф в точке М определяется двумя касательными t₁ и t₂, проведенными к двум кривым линиям l₁, и l₂ поверхности, проходящим через точку М (см. рис.75а).

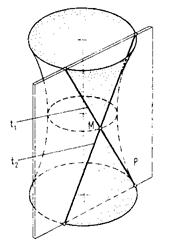
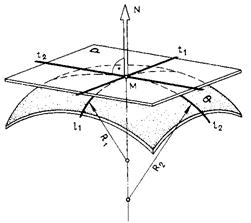
Рисунок 75 – Построение касательной к: а – выпуклой поверхности;

б -вогнутой поверхности.

В дифференциальной геометрии доказывается, что касательные t₁ и t₂ к двум кривым, проведенным на поверх­ности через точку М и имеющим экс­тремальные значения кривизны (макси­мальную и минимальную), образуют между собой прямой угол и являются так называемыми главными направле­ниями.

Максимальный и минимальный ра­диусы кривизны линий в точке касания М называются главными радиусами R₁ и R₂ кривизны поверхности в данной точке М, а их центры — центрами кри­визны поверхности в рассматриваемой точке. Величины, обратные главным ради­усам кривизны K₁ = l/R₁ и K ₂= l/R₂, называются главными кривизнами по­верхности в данной точке. Главные кривизны имеют одинаковые знаки, ес­ли главные радиусы кривизны R₁ и R₂ направлены в одну сторону, и разные зна­ки, если главные радиусы кривизны на­правлены в противоположные стороны.

Кривизна поверхности характери­зуется полной или га­уссовой кривизной. Полной или гаус­совой кривизной К поверхности в дан­ной точке называется произведение главных кривизн в рассматриваемой точке: К = К₁× К₂ = l/R₁× l/R₂.

Рассмотрим три случая касания плоскости к поверхности и кривизну поверхности в окрестности точки каса­ния.

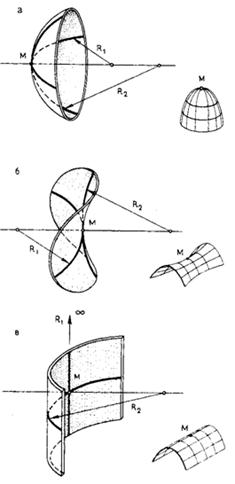
1. Касательная плоскость может иметь с поверхностью одну точку каса­ния М (рис.75а, 76а). В этом случае все линии поверхности, пересекающие­ся в данной точке, находятся по одну сторону касательной плоскости. При этом, если соприкасающийся параболо­ид в рассматриваемой точке является эллиптическим, то эту точку называют эллиптической. Поверхности, состоя­щие только из эллиптических точек, например эллипсоид и параболоид вра­щения, называют выпуклыми.

Главные кривизны имеют одинако­вые знаки, так как главные радиусы кривизны R₁ и R₂ направлены в одну сторону; в этом случае полная гауссова кривизна К > 0. Поверхности этого ви­да называют поверхностями положи­тельной кривизны, имеющей перемен­ный характер. Поверхностью постоян­ной положительной кривизны является только сфера.

2. Касательная плоскость к поверх­ности в данной точке М может пересекать поверхность по двум прямым ли­ниям. Так, например, в случае дважды линейчатой поверхности — гиперболи­ческого параболоида или однополостного гиперболоида вращения (см. рис. 76б) касательная плоскость пересекает эти поверхности по двум прямым обра­зующим l₁ и l ₂, которые, вместе с тем, являются их касательными t₁ и t₂, определяющими касательную плоскость Р.

Главные кривизны имеют разные знаки, так как главные радиусы кривиз­ны R₁ и R₂ направлены в противополож­ные стороны (рис. 76б). Полная гаус­сова кривизна К < 0. Поверхности это­го вида называют поверхностями отри­цательной кривизны, имеющей пере­менный характер.

3. Касательная плоскость касается поверхности по прямой образующей. Следовательно, все точки образующей имеют общую касательную плоскость рис. 76в).

Полная гауссова кривизна К = О, так как один из радиусов R₁ бесконечно большой, то их произведение обратится в нуль независимо от величины другого радиуса. Поверхности этого вида назы­вают поверхностями нулевой кривизны.

Построение плоскостей, касатель­ных к поверхностям. Плоскости, касательные к по­верхности, могут быть построены при различных исходных условиях. Каса­тельная плоскость может быть проведе­на различными способами. Назовем неко­торые из случаев, с которыми придется встретиться:

а) через точку, лежащую на линейчатой поверхности;

б) через точку, принадлежащую нелинейчатой поверхности вращения;

в) через точку, заданную вне поверхности;

г) парал­лельно прямой, заданной вне поверхно­сти.

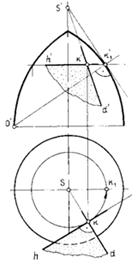
Пример. Построить плоскость, ка­сательную к поверхности вращения (то­ру), в заданной на ней точке К' (рис. 77). Если точка задана одной проекцией, вторую проекцию определяем с по­мощью вспомогательной параллели (окружности), которую проводим на по­верхности через данную точку. Через точку К проведены две прямые – КН и KD, задающие касательную плоскость. Одна из них касательна к проведенной параллели (она является горизон­талью), а другая должна быть касатель­ной к меридиану. Для построения этой касательной KD меридиан вращением совмещен с главным меридианом.

В этом положении к нему через точку s' проведена касательная под прямым уг­лом к прямой о'к'₁. Точка о' является центром дуги окружности — главного меридиана тора. Касательную продол­жим до пересечения с осью тора, а затем повернем в первоначальное положение. Две прямые — горизонталь КН и каса­тельная KD — определяют искомую касательную плоскость.

Пересечение поверхности вращения плоскостью. Конические сечения. В зависимости от расположения секущей плоскости по отноше­нию к оси прямого кругового конуса могут образоваться: пересекающиеся прямые, окружность, эллипс, парабола и гипербола (рис. 78а).

На рис 78б приведена общая схе­ма, наглядно показывающая скачкооб­разный характер видоизменений кони­ческих кривых и границы области обра­зования той или иной кривой в зависи­мости от положения (наклона) секущей плоскости относительно конуса. Как видно из схемы, размеры этой области у окружности и параболы чрезвычайно малы — здесь и возникает качествен­ный скачок, в то время как у эллипса и гиперболы размеры области, напротив, велики.

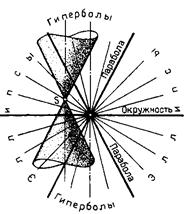
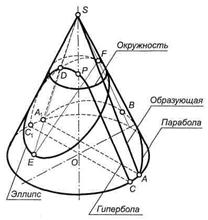
Рисунок 78 –Сечения конуса плоскостями

Построение линии пересечения по­верхностей вращения плоскостью. Ли­ния пересечения кривой поверхности плоскостью представляет собой пло­скую кривую линию (сечение), для по­строения которой необходимо опреде­лить отдельные точки сечения и соеди­нить их последовательно плавной кри­вой.

Чтобы построить линию пересече­ния линейчатой поверхности враще­ния плоскостью, необходимо опреде­лить точки пересечения отдельных об­разующих этой поверхности плоско­стью. Таким образом, задача на определение линии пересечения линейчатой поверхности плоскостью сводится к многократному решению задачи на пе­ресечение прямой с плоскостью.

Для построения точек линии пере­сечения нелинейчатой кривой поверх­ности плоскостью применяют основной способ — способ вспомогательных се­кущих плоскостей. Вспомогательные секущие плоскости проводят так, чтобы поверхность пересекалась по графиче­ски простым линиям. Точки пересече­ния этих линий будут искомыми точка­ми линии пересечения.

Рассмотрим примеры построения линии пересечения поверхностей вра­щения плоскостью. При построении се­чений следует выделить частный слу­чай, когда секущая плоскость является проецирующей или пересекаемая по­верхность занимает проецирующее по­ложение относительно плоскости про­екций и одна проекция линии пересече­ния известна.

Пример. Построить пересечение конуса фронтально проецирующей пло­скостью (рис.79). Секущая плоскость является проецирующей, поэтому фронтальная проекция линии сечения совмещена с проецирующим следом плоскости P_v. Полученный в сечении эллипс проецируется на плоскость V отрезком прямой a ' — b ', который являет­ся большой осью эллипса. Горизонталь­ная проекция оси строится с помощью линий связи. Малая ось эллипса m — n перпендикулярна большой оси и делит ее пополам. Точки m и n строим с по­мощью параллели или двух образую­щих конуса. На чер­теже построен действительный вид се­чения конуса способом замены плоско­стей проекций. Дополнительные точки сечения могут быть построены анало­гично построению точек m и n.

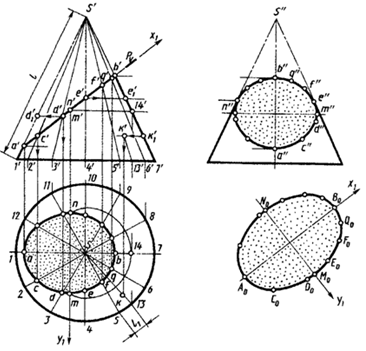
Рисунок 79 -Сечение конуса фронтально проецирующей пло­скостью

Аналогично решается задача на построение линии пересе­чения прямого кругового цилиндра фронтально проецирующей пло­скостью (рис.80).

Пересечение прямой линии с кривой поверхностью. Прямая линия может пересекать по­верхность в двух и более точках, может касаться ее. Если прямая не имеет об­щих точек с поверхностью, это означа­ет, что она не пересекает поверхность. Этапы решения этой задачи аналогич­ны описанному ранее постро­ению пересечения прямой с плоскостью и многогранной поверхностью.

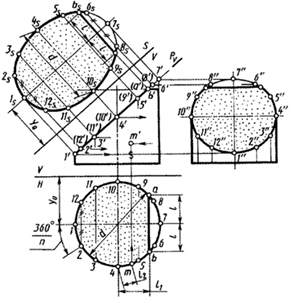
Рисунок 80 -Сечение цилиндра фронтально проецирующей пло­скостью

Чтобы найти точки пересечения прямой линии с кривой поверхностью (рис. 81 ), следует провести через данную прямую вспомогательную се­кущую плоскость и построить линию пересечения вспомогательной плоско­сти с данной поверхностью. Точки пе­ресечения прямой с построенной ли­нией сечения поверхности и будут ис­комыми точками.

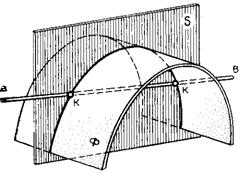
Рисунок 81 – Нахождение точки пересечения прямой с кривой поверхность

Обычно в качестве вспомогательной плоскости выбирают проецирующую плоскость. Однако в отдельных случаях следует принимать плоскость общего положения с тем, чтобы проекции сече­ния имели графически простую форму — прямые линии или окружности.

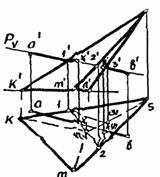
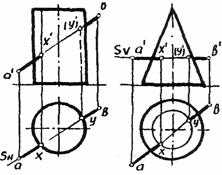
Рисунок 82 – Нахождение точек пересечения прямой с поверхностями с помощью плоскостей частного положения

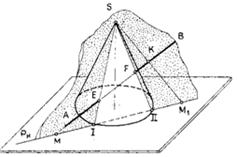
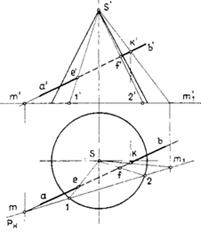
Рисунок 83 – Пересечение прямой общего положения с конусом модель и эпюр

Пример 1. Построить точки пересе­чения прямой с конической поверхно­стью (рис.83). Если выбрать в качестве вспомогательных проецирующие пло­скости, то сечениями поверхности бу­дут кривые линии — гипербола или эл­липс. Поэтому для определения точек пересечения прямой с поверхностью ко­нуса через данную прямую следует про­вести вспомогательную плоскость об­щего положения, которая пересекла бы поверхность конуса по образующим. Такая плоскость должна быть проведе­на через данную прямую и вершину ко­нуса.

Чтобы определить образующие, по которым плоскость пересекает конус, построим след секущей плоскости на плоскости основания конуса (в данном примере — на плоскости Н) с помощью вспомогательной прямой SKM₁ Через два горизонтальных следа прямых пройдет след Р_н секущей плоскости. Ис­комые образующие конуса S1 и S2 оп­ределяем в пересечении горизонталь­ного следа плоскости с окружностью ос­нования конуса. Дальнейшие построе­ния понятны из чертежа.

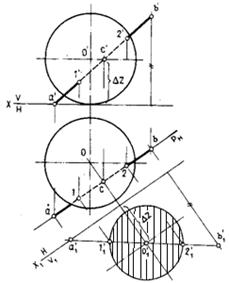Пример 2. Построить точки пересе­чения прямой с поверхностью сферы (рис.84). Через прямую проведена го­ризонтально проецирующая плоскость Р. Она пересекает сферу по окружно­сти, которая на фасаде изображается эллипсом. Чтобы избежать построения эллипса, применим способ замены пло­скостей проекций и примем за новую фронтальную плоскость проекций пло­скость V_x, параллельную секущей пло­скости. Построим на новой плоскости V_i проекцию заданной прямой и окруж­ность сечения сферы, отложив высоту ее центра — аппликату Az. Получен­ные точки пересечения проекции пря­мой с контуром сечения переносятся за­тем на исходные проекции. На плане будут видимыми точки, расположенные выше экватора сферы (точка 2), а на фасаде — точки, размещающиеся на передней половине сферы.

Взаимное пересечение поверхностей. Основной способ построения линии пересечения поверхностей — способ вспомогательных секущих поверхно­стей (плоскостей). Он аналогичен по­строению линии пересечений двух пло­скостей общего положения, рассмот­ренному ранее. Сущность этого способа заключается в том, что обе заданные поверхности пересекаются вспомогательной третьей поверхностью (обычно плоскостью или сферой), затем строятся линии пересечения первой заданной поверхности с третьей, второй заданной поверхности с третьей и в пересечении этих линий отмечаются точки, принадлежащие как первой, так и второй заданным поверхностям, то есть точки, принадлежащие линии их пересечения.

Вспомогательные секущие поверхности выбираем в зависимости от:

- условия задачи,

- вида пересекающихся поверхностей,

- расположения пересекающихся поверхностей относительно плоскостей проекций.

Положение вспомогательных секущих поверхностей выбирают так, чтобы они пересекали заданные по­верхности по графически простым ли­ниям — прямым или окружностям.

Построения выполняют в такой по­следовательности (рис.85): 1) проводят вспомогательную проецирующую пло­скость S, пересекающую заданные поверхности; 2) строят линии 1 — 2 и 3 — 4 пересечения вспомогательной пло­скости с заданными поверхностями Σ и Ф; 3) определяют точку К пересечения вспомогательных линий 1 — 2 и 3 — 4.

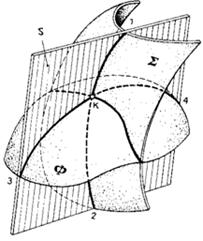
Рисунок 85 – Взаимное пересечение криволинейных поверхностей

Поскольку точка К одновременно принадлежит обеим вспомогательным линиям и, следовательно, пересекаю­щимся поверхностям, то она является точкой, принадлежащей искомой линии пересечения. Проведя несколько вспомо­гательных секущих плоскостей, полу­чим ряд точек линии пересечения. Их следует соединить плавной кривой в оп­ределенной последовательности. Про­екции линии пересечения должны рас­полагаться в пределах очерков как од­ной, так и другой поверхности одновре­менно.

Построение линии пересечения по­верхностей начинают с определения ха­рактерных ее точек — экстремальных (высшей и низшей) и точек видимости, отделяющих видимую часть линии пе­ресечения от невидимой. Приступая к построению линии пересечения повер­хностей, следует выделить более про­стой случай, когда одна из пересекаю­щихся поверхностей занимает проеци­рующее положение относительно пло­скости проекций и решение задачи уп­рощается.

Взаимное пересечение многогранных и кривых поверхностей. Многогранная и кривая поверхности пересекаются по ломанным кривым линиям, звенья которых (плоские кривые) – линии пересечения граней многогранной поверхности с кривой поверхностью, а точки излома – точки встречи ребер многогранника с кривой поверхностью. Решение задач на построение проекций линий пересечения многогранной поверхности и кривой и сводится к построению проекций точек встречи ребер многогранника и проекций линии пересечения граней его с кривой поверхностью.

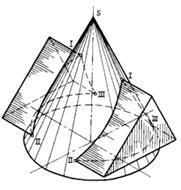
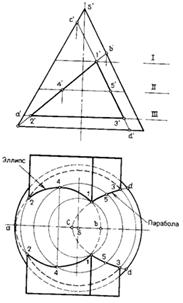
Рисунок 86 – Взаимное пересечение конуса и пирамиды

Пример 1. Построить пересечение трехгранной призмы с конусом враще­ния (рис.86). Три боковые грани приз­мы являются фронтально проецирую­щими плоскостями, следовательно, по­строение линии пересечения сводится к решению ранее рассмотренной задачи на пересечение поверхности проециру­ющей секущей плоскостью и прямой линией. Линия пере­сечения данных поверхностей пред­ставляет собой ломаную линию, состо­ящую из трех плоских кривых. Грани призмы пересекают поверхность кону­са по окружности, неполному эллипсу и неполной параболе. В данном случае вспомогательными плоскостями можно не пользоваться, так как фронтальные проекции точек линии пересечения из­вестны.

Горизонтальные проекции линий пересечения строим по точкам с по­мощью трех параллелей конуса, прове­денных через характерные точки линии пересечения. Промежуточная точка 4, 4' выбрана посредине отрезка а'b' ко­торый является большой осью эллипса.

Взаимное пересечение кривых поверхностей (поверхностей вращения). Две кривые поверхности в общем случае пересекаются по замкнутым пространственным кривым линиям, которые строятся по точкам, определяемым вспомогательными секущими плоскостями.

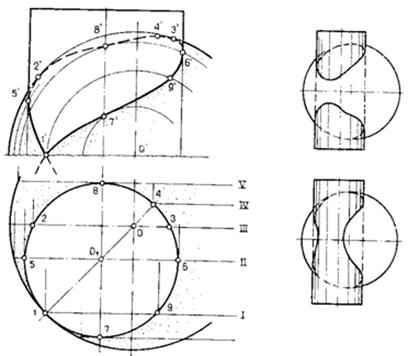
Пример 2. Построить линию пересе­чения цилиндра и сферы (рис.87, а). Боковая поверхность Цилиндра являет­ся горизонтально проецирующей, сле­довательно, горизонтальная проекция линии пересечения известна. Она сов­падает с проекцией боковой поверхно­сти цилиндра. Так как пересекаются две поверхности второго порядка, ли­нией пересечения будет пространст­венная кривая — кривая четвертого порядка.

а б

Рисунок 87 – Взаимное пересечение цилиндра с полушаром

Проведем несколько фронтальных вспомогательных плоскостей, которые пересекут цилиндр по образующим, а сферу — по окружностям, параллель­ным фронтальной плоскости проекций.

Характерными или опорными точ­ками (они выбираются на плане) явля­ются:

а) точки 1, 2 и 3, в которых проек­ции линии пересечения касаются гори­зонтального и фронтального очерков сферы, они определяются с помощью линий связи;

б) точка 4 — высшая, оп­ределяется на плане с помощью меридиана сферы, проходящего через ось цилиндра;

в) точки 5 и 6 — точки види­мости и касания кривой к очерковым образующим цилиндра;

г) точки 7 и 8 — определяют границы изменения проек­ции линии пересечения.

На рис. 87б приведены два других случая пересечения данных поверхно­стей при некотором изменении их взаи­моположения. В первом из них линия пересечения представляет собой две симметричные замкнутые кривые, во втором — отсутствует общая (узловая) точка самопересечения кривой. Отсюда следует, что два геометрических тела могут пересекаться полностью, тогда получим две замкнутые линии пересечения, или частично и тогда пересечение происходит по замкнутой линии.

Пример 3. Построить линию пересе­чения конической и сферической поверхностей (рис.88).

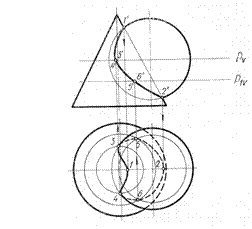Точки 1 и 2 линии пересечения отмечаем без дополнительных построений, так как они являются характерными точками проек­ции линии пересечения полученными по чертежу. Их горизонтальные проекции определяются с помощью линий связи. Для нахождения проекций точек 3, 4 и 5, 6 проводились вспомогательные горизонтальные секущие плоскости Р и Р₁, причем одна из них (Р) проведена через центр шара, благодаря чему получены проекции точек 3 и 4 – характерных точек, определяющих границу видимости линии пересечения на горизонтальной плоскости проекций.

Метод сфер. Применение в качестве вспомогательных секущих поверхностей концентрических сфер при построении линии пересечения двух кривых поверхностей возможно при соблюдении следующих трех условий:

1. обе пересекающиеся поверхности должны быть поверхностями вращения;

2. оси пересекающихся поверхностей должны пересекаться (не скрещиваться);

3. оси пересекающихся поверхностей должны быть параллельными одной из плоскостей проекций.

Дело в том, что сфера, центр которой находится на оси любой поверхности вращения, пересекает эту поверхность по окружности, а если при этом ось поверхности вращения параллельна какой-либо плоскости проекций, то эта окружность спроецируется на нее в виде отрезка прямой линии (рис. 89), точное построение которого не вызывает никаких затруднений.

Пример 1. Построить линию пересе­чения двух прямых круговых конусов при помощи вспомогательных секущих концентрических сфер (рис.90).

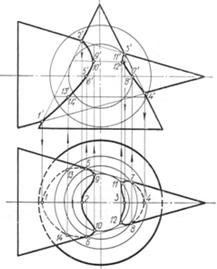В рас­сматриваемом случае пересекаются два пря­мых круговых конуса, оси которых пересека­ются и параллельны плоскости проекций V. Проекции точек 1, 2, 3, 4 линий пересечения отмечены при помощи линий связи, проекции характерных точек 5, 6 и 7, 8 определены вспо­могательной секущей горизонтальной плоско­стью Р, проведенной через ось конуса, которая расположена перпендикулярно к плоскости проекций W, точек 9, 10 и 11, 12 — вспомога­тельной секущей сферой, проведенной касательной к поверхности конуса с осью, перпен­дикулярной к плоскости проекций Н (наимень­шей сферы), проекции точек 13 и 14 — вспомо­гательной сферой большего диаметра. Постро­ения понятны из чертежа.

Пример 2. Построить линию пересе­чения прямого кругового конуса и наклонного цилиндра при помощи вспомогательных секущих концентрических сфер (рис.91).

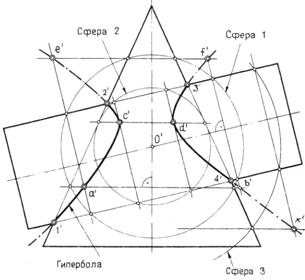
Рисунок 91 – Взаимное пересечение конуса и цилиндра

В данном примере оси поверхностей вращения пере­секаются и параллельны плоскости проекций (рис. 91). Для построения линии пересечения в данном случае нецелесообразно использовать вспомо­гательные секущие плоскости. Они не могут дать вспомогательные линии се­чения, которые проецировались бы графически простыми линиями. Поэтому для построения линии пересечения по­верхностей вращения с пересекающи­мися осями и общей плоскостью сим­метрии параллельной плоскости проек­ций следует применить так называемый способ вспомогательных концентриче­ских сфер.

Прежде чем приступить к построе­ниям, отметим четыре общие точки 1^/ - 2^/ - 3^/- 4^/ цилиндра и конуса в пересечении очерковых образующих — главных меридианов поверхностей. При­мем точку О пересечения осей за центр концентрических сфер. Проведем из центра О ^/ вспомогательную секущую сферу 1 произвольного радиуса. Она пе­ресечет каждую из поверхностей по двум параллелям, как это показано на рис. 93. Эти параллели принадлежат одной поверхности — сфере 1, следова­тельно, точки их пересечения одновре­менно принадлежат и двум данным по­верхностям — конусу и цилиндру, т. е. принадлежат линии их пересечения. Выбирая иной радиус вспомогательной сферы, можно построить любое число точек линии пересечения. Каждое сфе­рическое сечение в общем случае опре­деляет восемь точек линий пересече­ния, попарно совпадающих (а^/, b,^/ е^/, f^/ ) на фронтальной проекции.

Проведем сферу 2 наименьшего ра­диуса, которая пересечет цилиндр по двум параллелям и коснется конуса. Это сечение определяет четыре харак­терные точки противоположных частей линии пересечения, наиболее близко расположенные. Чтобы уточнить вид кривой, проведем еще одну вспомога­тельную сферу 3, изобразив частично ее меридиан и параллели. Получим еще две совпадающие проекции точек (к ').

Необходимо отметить следующую закономерность: если оси поверхностей вращения второго порядка пересека­ются и параллельны плоскости проек­ции у то линия их пересечения проеци­руются на эту плоскость в виде пло­ской кривой второго порядка.

Пространственная кривая линии пересечения конуса и цилиндра проецируется на плоскость, параллельную их плоскости симметрии, в виде гипер­болы.

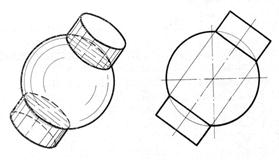
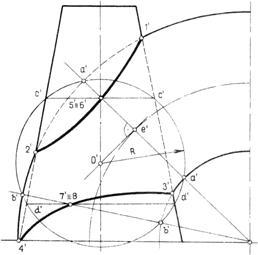Пример 3. Построить линию пересе­чения прямого усеченного кругового конуса и тора при помощи вспомогательных сферических сечений способом эксцентрических сфер (рис.92).

Для решения задачи необходимо построить вспомогательную сферу, которая пересечет обе поверхности по окружности. Проведена фронтальная проекция а^/а^/ окружности тора, которую можно принять за линию пересечения тора вспомогательной сферой. Затем через середину ее проекции проведена прямая е^/о^/, перпендикулярная к ней, до пересечения с осью конуса в точке о^/.

Из точки о^/ проводят вспомогательную сферу радиуса о^/а^/, которая пересечет тор также по второй окружности b^/b^/, а конус – по двум окружностям с^/с^/ и d^/d^/. Каждая пара окружностей пересекается в двух общих точках 5^/≡6^/ и 7^/≡8^/, принадлежащих линиям пересечения поверхностей конуса и тора. Взяв другое сечение тора, найдем новые точки. Линия пересечения поверхностей проходит через точки 1^/, 2^/ и 3^/, 4^/.

Некоторые особые пересечения поверхностей второго порядка. В некоторых случаях расположение, форма или соотноше­ния размеров криволинейных поверхностей таковы, что для изображения линии их пересечения никаких сложных построе­ний не требуется. Рассмотрим некоторые такие случаи.

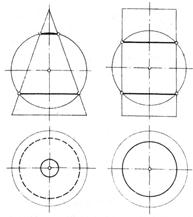
1. Оси двух пересекающихся повер­хностей вращения совпадают (рис. 93). Две поверхности вращения заданы одной осью и главными меридианами. Такие поверхности называют соосными. Точки пересечения меридианов при вращении вокруг оси описывают парал­лели, которые принадлежат обеим по­верхностям. Следовательно, две соосные поверхности вращения пересека­ются по параллелям; при этом, если оси поверхностей параллельны плоско­сти проекции, то параллели проециру­ются на эту плоскость прямыми ли­ниями, перпендикулярными проекции оси.

2. Пересечение поверхностей, описанных вокруг одной сферы (рис.94). При этом условии линии их пересечения распадаются также на две плоские кривые.

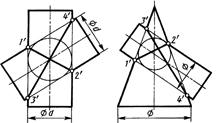
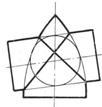
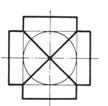
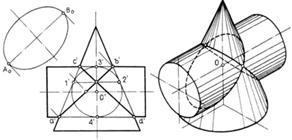
В случаях, показанных на рис. 94, поверхности двух цилиндров, конуса и цилиндра, тора и цилиндра пересекаются по двум эллип­сам.

Дата добавления: 2014-01-05