Основные понятия недетерминированных конечных автоматов

Тема 5.3. Недетерминированные конечные автоматы

Резюме по теме

Вопросы для повторения

1.Детерминированный конечный автомат это?

2.Что называется диаграммой автомата?

3.Под программой автомата понимается?

4.В каком случае язык называется конечно-автоматным?

Приведены основные понятия детерминированных конечных автоматов. Выявлено понятие программы автомата, а так же диаграммы и конфигурации детерминированного автомата. Рассмотрена схема доказательства правильности автомата, которая позволяет судить о работоспособности автомата. Продемонстрировано произведение автомата.

Цель: ознакомиться с недетерминированными конечными автоматами и способом их детерминизации.

Задачи:

1. Рассмотреть недетерминированные конечные автоматы.

2. Рассмотреть детерминизацию недетерминированного конечного автомата.

Рассматриваемые недетерминированные конечные автоматы являются обобщениями детерминированных: они при чтении очередного символа на входе могут выбрать в качестве следующего одно из нескольких состояний, а кроме того, могут изменить состояние без чтения входа. Основной результат, который мы установим, утверждает, что это обобщение не существенно: недетерминированные и детерминированные конечные автоматы распознают одни и те же языки.

Недетерминированный конечный автомат (НКА) - распознаватель - это система вида

M =< Σ, Q, q₀, F, Φ >,

включающая следующие компоненты:

Σ = {a₁,..., a_m} (m ≥ 1) конечное множество - входной алфавит;

Q = {q₀,..., q_n−1^}(n ≥ 1) конечное множество - алфавит внутренних состояний;

q₀Q начальное состояние автомата;

F Q множество принимающих (допускающих, заключительных) состояний;

Φ:Q Ч (Σ 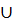{ε}) → 2^Q функция переходов. Для a Σ значение Φ(q, a) - это множество состояний в каждое из которых может перейти автомат из состояния q, когда получает на вход символ a. Φ(q, ε) - это множество состояний в каждое из которых может перейти автомат из состояния q без чтения символа на входе.

Как и для детерминированных автоматов, функцию переходов можно представить с помощью набора команд-программы: для каждой пары q Q и a Σ и каждого состояния q^’ Φ(q, a) в программу помещается команда qa → q^’, и для каждого состояния q^’ Φ(q, ε) в программу помещается команда q → q^’. Отличие от детерминированного случая состоит в том, что для одной пары q Q и a Σ в программе может быть несколько команд вида qa → q^’ или не быть ни одной такой команды. Кроме того, могут появиться ε-команды (пустые переходы) вида q → q^’, означающие возможность непосредственного перехода из q в q^’ без чтения символа на входе.

При табличном задании функции Φ в таблице появляется (m + 1)- ый столбец, соответствующий пустому символу ε и на пересечении строки q и столбца a (Σ 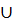{ε}) стоит множество состояний Φ(q, a).

Для недетерминированного автомата M =<Σ, Q, q₀, Φ > в диаграмме D_M=(Q, E) с выделенной начальной вершиной q₀ и множеством заключительных вершин F ребра взаимно однозначно соответствуют командам: команде вида qa → q^’ (a 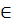Σ) соответствует ребро (q, q^’), с меткой a, а команде вида q → q^’ cоответствует ребро (q, q^’), с меткой ε.

Скажем, что заданный последовательностью ребер путь p = e₁e₂... e_T в диаграмме D_M несет слово w = w₁w₂... w_t (t ≤ T), если после удаления из него пустых ребер (т.е. ребер с метками ε) остается последовательность из t ребер p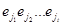^’ = метки которых образуют слово w, т.е. w_i это метка ребра 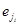1(≤i≤t). Очевидно, это эквивалентно тому, что последовательность меток на ребрах пути p имеет вид 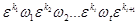, где k_j≥ 0 (j = 1, 2,..., t + 1) и t + .

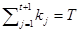Слово w переводит q в q^’ в диаграмме D_M, если в ней имеется путь из q в q^’ который несет w.

На недетерминированные автоматы естественным образом переносится определение конфигураций и отношения перехода между ними.

Конфигурация НКА M =< Σ, Q, q₀, F, Φ, > - это произвольная пара вида (q, w), в которой q Q и w 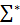. Определим отношение 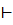_M перехода из одной конфигурации в другую за один шаг:

(q, w) 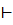_M(q’, w’) 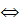(w = aw’ и q’ Φ(q, a)) или (w = w’ и q’ Φ(q, ε)).

Как и для ДКА, через 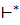_M обозначим рефлексивное и транзитивное замыкание отношения 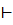_M.

Внешне определение распознавания слов НКА совпадает с определением для ДКА.

НКА M распознает (допускает, принимает) слово w, если для некоторого q F (q’, w) 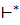_M(q, ε).

Язык L_M, распознаваемый НКА M, состоит из всех слов, распознаваемых автоматом:

L_M= {w | M распознает w}.

Отличие состоит в том, что у НКА может быть несколько различных способов работы (путей вычисления) на одном и том же входном слове w. Считаем, что НКА распознает (допускает, принимает) это слово, если хотя бы один из этих способов приводит в заключительное состояние из F.

Из определения диаграммы D_M непосредственно следует, что НКА M распознает слово w, тогда и только тогда, когда существует такое заключительное состояние q F, что в диаграмме D_M слово w переводит q₀ в q. Иными словами, в D_M имеется путь из q₀ в q, на ребрах которого написано слово w (с точностью до меток ε).

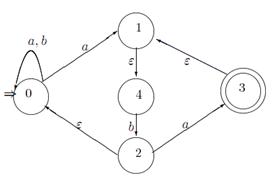Пример 1. Рассмотрим НКА N₁=<{a,b},{0,1,2,3,4},0,{3}, Φ>, где его диаграмма D_N1 представлена на рис. 5.15.

Рис. 5.15. Таблица функции переходов и диаграмма НКА

Рассмотрим работу этого автомата на слове ababa:

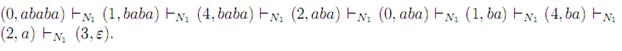
Так как 3 - заключительное состояние, то ababa L_N1 ^. Заметим, что у автомата N₁ имеются и другие способы работы на этом слове, не ведущие к заключительному состоянию. Например, он может после чтения каждого символа оставаться в состоянии 0. Но чтобы слово допускалось, достаточно существовать хотя бы одному хорошему способу.

Дата добавления: 2014-01-05