Конкретная математика

Определение наилучшей альтернативы

Итоговый вес (приоритет) альтернативы A_i вычисляется согласно следующей формуле:

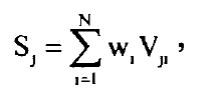
где S — показатель качества j-й альтернативы; Wi— вес i-ro

критерия; Vji— важность j-й альтернативы по i-му критерию.

Для трех площадок проведенные вычисления позволяют определить:

SA= 0,65 ® 0,69 + 0,22 ® 0,07 + 0,13 ® 0,68 = 0,552;

SB = 0,65 ® 0,19 + 0,22 ® 0,65 + 0,13 <8) 0,09 = 0,278;

SK= 0,65 ® 0,12 + 0,22 ® 0,28 + 0,13 ® 0,23 = 0,17.

Итак, альтернатива А оказалась лучшей.

(Лекции 2004, фрагменты)

Санкт-Петербург

09.05.2004

Докажем, что число счастливых 2n-значных трамвайных билетов равно

.

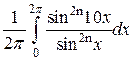Билет считается счастливым, если сумма первых n цифр его номера равна сумме n последних цифр, например, билет с номером 764395 – счастливый шестизначный билет.

Упражнение. Докажите, что функция от параметра n, вычисляющая число счастливых 2n-значных трамвайных билетов, примитивно рекурсивна.

Доказательство (леммы).

Рассмотрим равенство (1+z+…+z⁹)ⁿ=, тогда а_i определяет количество n-значных чисел, сумма цифр которых равна i.

Нам нужно вычислить .

Имеем (1+z+…+z⁹)ⁿ(1+z^-1+…+z^-9)ⁿ=´=,

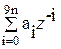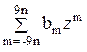тогда b₀=.

(1+z+…+z⁹)ⁿ(1+z^-1+…+z^-9)ⁿ==.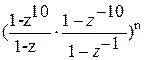

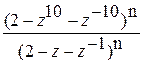Известно, что =.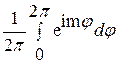

Пусть z=e^ij=cosj+isinj, тогда b₀===.

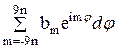Преобразуем =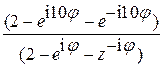

=

==.

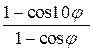Таким образом,

b₀===.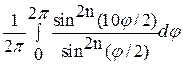

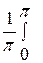
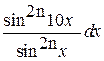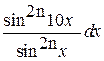При доказательстве тех или иных комбинаторных тождеств часто используется одно или одновременно два из следующих правил:

Правило суммы. Если объект А может быть выбран m способами, а объект В другими n способами, то выбор “либо А, либо В” может быть осуществлен m+n способами.

Правило произведения. Если объект А может быть выбран m способами и после каждого из таких выборов объект В в свою очередь может быть выбран n способами, то выбор “А, и В” в указанном порядке может быть осуществлен m×n способами.

Примеры. На основе этих правил в курсе математического анализа легко были получены формулы для числа k-перестановок 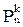и числа k-сочетаний 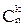из n объектов, а именно

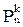= n(n-1)…(n-k+1)

=

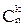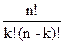
Упражнение. Докажите, что число k-перестановок из n объектов с повторениями равно n^k.

Задача. Доказать, что число k-сочетаний из n объектов с повторениями равно .

Решение (Л. Эйлер): Пусть X={1,2,…n} и рассмотрим любое из k-сочетаний с повторениями с₁с₂…с_k этих n чисел (считаем, что в сочетании с₁с₂…с_k элементы выписаны в неубывающем порядке). Естественно, что в каждом сочетании вследствие возможности неограниченных повторений любые рядом стоящие элементы могут быть одинаковыми. Ввиду этого обстоятельства строим с помощью соотношений

d₁=c₁+0; d₂=c₂+1;…; d_i=c_i+i-1;…; d_k=c_k+k-1

последовательность элементов d₁d₂…d_k следовательно, при любых элементах c_i элементы d_i всегда различны. Ясно, что отображение с₁с₂…с_k в d₁d₂…d_k биективно. Число последовательностей из элементов d_i равно числу k-сочетаний без повторений из элементов от 1 до n+k-1, т. е. .

Дата добавления: 2014-01-06