Вид корней характеристического уравнения и устойчивость

Теоремы А.М. Ляпунова

При использовании линеаризации (что делалось и до Ляпунова) всегда возникало сомнение в правомерности получаемых результатов. Две теоремы Ляпунова дали строгое обоснование метода первого приближения, предложенного им в 1893 г.

Теорема 1 утверждает, что при характеристическом уравнении первого приближения, имеющем корни только с отрицательными вещественными частями, невозмущенное движение устойчиво и притом асимптотически, каковы бы ни были нелинейные функции в правой части исходного уравнения.

Теорема 2 утверждает, что если в числе корней характеристического уравнения первого приближения имеются корни, вещественные части которых положительны, то невозмущенное движение неустойчиво, каковы бы ни были нелинейные функции в правой части исходного уравнения.

Случай, когда характеристическое уравнение не имеет корней с положительной вещественной частью, но имеет хотя бы один корень с нулевой вещественной частью, является особым случаем. В особых случаях по корням характеристического уравнения линеаризованной системы нельзя сделать заключение об устойчивости или неустойчивости реальной (исходной) системы. Для получения такого заключения необходимы дополнительные исследования вида нелинейной функции (исследование членов уравнения, отброшенных при линеаризации) или

привлечение к анализу физических соображений.

Анализ устойчивости установившегося состояния системы при малых отклонениях от состояния равновесия, сводится к анализу корней характеристического уравнения, обычно имеющего для современных автоматически регулируемых систем высокий порядок:

D(p) = a₀×pⁿ + a₁×p^n-1 + a₂×p^n-2 + …+ a_n-1×p + a_n = 0.

Если p₁, p₂ , …, p_n - корни этого уравнения, то его решение, описывающее свободный переходный процесс в электрической системе, характеризуемый изменением любой переменной x во времени (наиболее характерной является угол между вектором ЭДС генератора и вектором напряжения на шинах принимающей системы) имеет вид:

x(t) =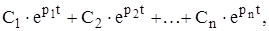

где С₁, С₂, …, С_n – постоянные, зависящие от начальных условий.

Корни характеристического уравнения могут быть комплексными попарно сопряженными 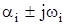или действительными a_i.

Каждому действительному корню a_i в решении будет соответствовать слагаемое вида 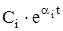. Если a_i < 0, то слагаемое вида 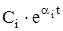с течением времени затухает (рис. 20, а); если a_i = 0, то 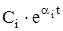неизменно (рис. 20, б); если a_i > 0, то 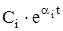c течением времени неограниченно возрастает (рис. 20, в).

Каждой паре комплексно сопряженных корней в решении будет соответствовать два слагаемых вида

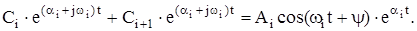
Если a_i < 0, то эти слагаемые представляют собой затухающее колебание (рис. 21, а), если a_i = 0, то гармоническое колебание постоянной амплитуды (рис. 22, б) и если a_i > 0, то колебание с неограниченно возрастающей амплитудой

(рис. 22, в).

Так как решение x(t) представляет собой сумму слагаемых вида 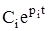, то достаточно лишь одному действительному корню p_i = a_i иметь положительное значение или двум комплексным корням 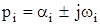иметь положительную действительную часть, как переменная, характеризующая свободный переходный процесс, будет с течением времени неограниченно возрастать, т.е. исследуемая система будет неустойчива.

Рисунок 20 – Переходные процессы при комплексных корнях характеристического уравнения

Если все действительные корни и все действительные части комплексных корней будут отрицательны, то система будет возвращаться в исходное состояние, т.е. она будет устойчива.

Если по осям декартовых координат отложить jw и a, то корни в этой плоскости изобразятся точками (рис. 22). Эту плоскость называют плоскостью корней.

Рассматривая корни характеристического уравнения как точки комплексной плоскости, условие устойчивости формулируют следующим образом: “ Для того чтобы состояние равновесия было устойчиво, необходимо и достаточно, чтобы все корни характеристического уравнения лежали в левой полуплоскости

корней”.

Коэффициенты характеристического уравнения зависят от параметров системы. Параметры системы, особенно режимные параметры, претерпевают в процессе работы изменения. При изменении коэффициентов характеристического уравнения корни его перемещаются на комплексной плоскости.

При некоторых значениях коэффициентов один действительный корень может оказаться в начале координат или пара комплексных корней - на мнимой оси, что определяет границу устойчивости.

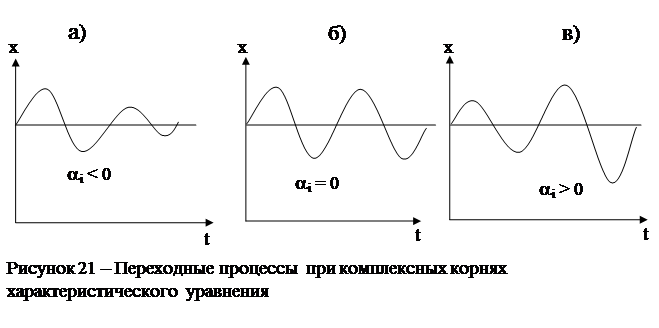
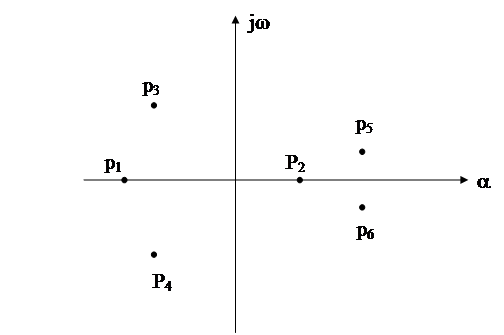
Рисунок 22 – Плоскость корней

Переход одного действительного корня или пары комплексных корней через

мнимую ось приведет к нарушению устойчивости системы.

Дата добавления: 2014-01-06