Случайные величины

К случайным величинам в энергетике относятся такие важные параметры как спрос на электрическую мощность и электроэнергию, отклонения частоты и напряжения от номинальных значений, располагаемая мощность электростанций, мощность агрегатов в аварийном ремонте, длительность безаварийной работы отдельных агрегатов и т.д.

Знания закономерностей изменения этих случайных величин необходимо как при проектировании, так и при эксплуатации электроэнергетических систем.

Случайные величины можно разделить на два класса: дискретные и непрерывные. Дискретная случайная величина может принимать только дискретные (разрозненные) значения, например, число агрегатов, вышедших аварийно из работы. Это число в ограниченном интервале является конечным. Значения непрерывных случайных величин могут изменяться непрерывно, т.е. даже в ограниченных интервалах такие величины могут иметь бесконечно большое число значений, например, ошибка прогнозирования электрических нагрузок.

Появление тех или иных значений случайной величины можно рассматривать как события, а различным событиям в общем случае, как известно, соответствуют различные вероятности.

Рассмотрим дискретную случайную величину X с возможными значениями x₁, x₂, x₃… x_n.

Обозначим вероятности этих событий:

р₁ = P(X = x₁); р₂ = P(X = x₂); р₃ = P(X = x₃); …; р_n = P(X = x_n).

Так как эти события образуют полную группу, то

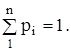
Если же множество значений случайной величины образует бесконечное, но

счетное множество, то ряд 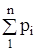сходится и его сумма равна 1.

Таким образом, суммарная вероятность, равная 1, распределена между всеми значениями случайной величины.

Законом распределения дискретной случайной величины называется всякое соотношение, устанавливающее связь между возможными значениями случайной величины и соответствующими вероятностями.

Простейшей формой задания этого закона является таблица, первая строка которой содержит возможные значения случайной величины (обычно в порядке возрастания), а вторая – соответствующие вероятности (см. табл. 10).

Такую таблицу называют рядом распределения случайной величины.

Пример 9. В энергетической системе имеется 4 однотипных генератора. Вероятность аварии каждогоиз нихq = 0,02, вероятность рабочего состояния р = 0, 98.

Будем считать случайной величиной количество аварийных агрегатов. Эта величина является дискретной и может принимать значения 0, 1, 2, 3, 4.

Произведя расчеты по формуле биномиального распределения (см. п. 5.3), получим следующую таблицу.

Число аварийных агрегатов
Вероятность pi	0,92237	0,07530	0,00230	0,00003	0,00000

Сумма вероятностей равна единице.

Чтобы придать ряду распределения более наглядный вид, часто прибегают к его графическому изображению: по оси абсцисс откладываются возможные значения случайной величины, а по оси ординат – вероятности этих значений. Для наглядности полученные значения соединяют отрезками прямых. Такая фигура называется многоугольником распределения (рис. 22).

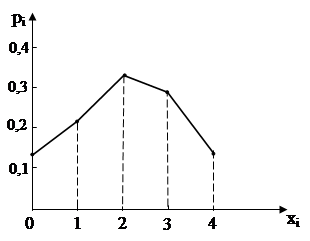Рисунок 22 – Многоугольник распределения

Закон распределения вероятностей непрерывных случайных величин нельзя представить в виде таблицы, так как число значений таких величин бесконечно даже в ограниченном интервале. Кроме того, для непрерывного распределения вероятность каждого отдельного значения случайной величины равна нулю, точнее, является бесконечно малой величиной. На этом и основано противопоставление непрерывных и дискретных распределений – ведь для последних вероятность, равная единице, распределена конечными положительными порциями. Для непрерывных та же единица распределена между бесконечным числом значений случайной величины и поэтому для каждого из них она будет бесконечно малой.

Поэтому для непрерывных случайных величин определяют вероятность попадания ее в некоторый интервал, который может быть принят как угодно малым.

Для количественной оценки вероятностей как непрерывных, так и дискретных случайных величин можно использовать функцию распределения F(x), которая равна вероятности того, что данная случайная величина X попадет в интервал значений от -¥ до некоторого фиксированного значения x, т.е. она меньше x:

F(x) =

Функцию F(x) называют также интегральной функцией распределения.

Для непрерывных случайных функция распределения задается аналитически, графически или в виде таблиц распределения.

По заданной функции распределения можно вычислить вероятность попадания непрерывной случайной величины в заданный интервал (x₁, x₂):

,

т.е. для того, чтобы определить вероятность попадания непрерывной случайной величины в интервал (x₁, x₂), где x₁ < x₂ , достаточно взять разность функций распределения при значениях x₂ и x₁.

Задание непрерывной случайной величины с помощью функции распределения не является единственным. Её можно задать с помощью другой функции, которая называется плотностью распределения вероятностей, которая определяется как первая производная функции F(x):

f(x) =

Функцию f(x) называют также дифференциальной функцией распределения.

В некотором смысле эта функция “более удобная”, чем интегральная функция F(x). Используя функцию F(x), трудно определить характер распределения случайной величины в небольшой окрестности той или иной точки числовой оси. Решить эту задачу позволяет плотность распределения вероятностей.

Рассмотрим основные свойства функции f(x).

1. Для функции f(x) имеет место равенство

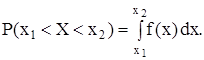(68)

2. Для любых x дифференциальная функция f(x) неотрицательна, т.е. f(x)0.

В энергетике применяют случайные величины со следующими распределениями вероятностей: нормальное, биномиальное, равномерное, экспоненциальное, распреде­­ление Пуассона и распределение Вейбулла. Области применения этих распределений рассмотрены ниже.

5.4 Числовые характеристики случайных величин

Для решения многих практических задач нет необходимости характеризовать случайную величину исчерпывающим образом. Зачастую бывает достаточно указать отдельные числовые параметры, которые позволяют в удобной, компактной форме отразить существенные особенности случайной величины.

Эти характеристики случайной величины, являющиеся не функциями, а числами, называют числовыми характеристиками случайной величины.

Наиболее важной характеристикой является математическое ожидание.

Математическим ожиданием дискретной случайной величины называется сумма произведений всех возможных значений случайной величины на вероятности этих значений:

Для непрерывной случайной величины математическое ожидание, естественно, выражается уже не суммой, а интегралом

где f(x) – плотность распределения случайной величины X.

Математическое ожидание связано следующей зависимостью со средним арифметическим измеренных или наблюдаемых значений случайной величины: при большом числе опытов среднее арифметическое найденных значений случайной величины приближается (сходится по вероятности) к ее математическому ожиданию.

Геометрически m_x представляет собой абсциссу центра тяжести площади, ограниченной кривой плотности распределения и осью абсцисс.

Математическое ожидание квадрата отклонения случайной величины X от центра ее распределения называется дисперсией.

Для непосредственно вычисления дисперсии служат формулы:

D_x = , (69)

(70)

По формуле (69) рассчитывается дисперсия дискретной, по формуле (70) - непрерывной случайной величины.

Квадратный корень из дисперсии называют средним квадратическим отклонением (иначе стандартным отклонением или стандартом).

.

Отношение стандартного отклонения к математическому ожиданию называют коэффициентом вариации:

5.5 Законы распределения дискретных случайных величин

Среди распределений дискретных случайных величин в электроэнергетике наиболее распространенными являются биномиальное и распределение Пуассона.

Биномиальное распределение применяется в тех случаях, когда исследуются однотипные объекты или процессы. Например, при оценке аварийности оборудования или определении числа дефектных деталей, при расчетах необходимого резерва оборудования, определении числа одновременно работающих электродвигателей, электронагревателей и других электроустановок, определении расчетных нагрузок однотипного оборудования и т. д.

Во многих практических случаях при многократных независимых испытаниях могут быть только два исхода: случайное событие А произойдет или не произойдет.

Пусть вероятность того, что в каждом из этих независимых испытаний событие А произойдет, равна p, где p – статистическая вероятность. Тогда вероятность противоположного события (событие А не происходит)

q = 1- p.

Зная р или q, можно определить вероятность того, что в n независимых испытаниях событие А, например повреждение агрегата, случится m раз. Обозначим эту вероятность через 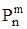. Она равна

,

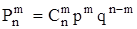где - число комбинаций из n элементов по m.

Число комбинаций вычисляется по формуле

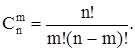
Распределение Пуассона применяется для описания простейших потоков однородных событий. Закон Пуассона - это закон редких явлений. Он выражает биномиальное распределение при большом числе опытов и малой вероятности события (обычно p < 0,1).

Распределение Пуассона играет важную роль в ряде вопросов физики, теории связи, теории надежности, теории массового обслуживания и т. д.

Допустим, что произведено большое число опытов n, в каждом из которых событие А имеет малую вероятность p. Тогда вероятность того, что событие А появится ровно m раз, может быть определена по формуле

, (71)

где a - параметр закона Пуассона, вычисляемый по формуле a = p×n.

Обычно формулу (71) используют, когда n > 100, а n×p < 10.

Пример 10. Некоторое устройство выходит строя, если откажет определенная микросхема. Вероятность ее отказа в течение 1 часа работы равна 0,001. Найти вероятность того, что в течение 3000 часов работы микросхему надо будет заменить не более 2 раз.

Р е ш е н и е. Среднее число отказов за 3000 часов работы

a = р×n = 0,001×3000 = 3

Вероятность безотказной работы устройства

0,0498

Вероятность одного отказа в течение 3000 часов

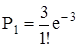= 0,1494

Вероятность двух отказов

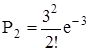=0,2240

Вероятность того, что число отказов будет меньше трёх:

P(m < 3) = 0,0498 + 0,1494 + 0,2240 = 0,4232

Дата добавления: 2014-01-06