Композиция графов

Пусть G₁(X,E₁) и G₂(X,E₂) — два графа с одним и тем же множеством вершин X. Композицией G₁(G₂) графов G₁ и G₂ называется граф с множеством вершин E, в котором существует дуга (x_i,x_j) тогда и только тогда, когда существует дуга (x_i,x_k), принадлежащая множеству E₁, и дуга (x_k,x_j), принадлежащая множеству E₂.

Рассмотрим выполнение операции композиции G₁(G₂) на графах, изображенных на рис.4.3. Для рассмотрения операции составим таблицу, в первом столбце которой указываются ребра (x_i, x_k), принадлежащие графу G₁, во втором — ребра (x_k, x_j), принадлежащие графу G₃, а в третьем — результирующее ребро (x_i, x_j) для графа G₁(G₂).

G1	G2	G1(G2)
(x1,x2)	(x2,x1) (x2,x3)	(x1,x1) (x1,x3)
(x1,x3)	(x3,x3)	(x1,x3)
(x2,x1)	(x1,x1) (x1,x3)	(x2,x1) (x2,x3)

Заметим, что дуга (x₁,x₃) результирующего графа в таблице встречается дважды. Однако, поскольку рассматриваются графы без параллельных ребер (дуг), то в множестве E результирующего графа дуга (x₁,x₃) учитывается только один раз, т.е. E = {(x₁,x₁), (x₁,x₃), (x₂,x₁), (x₂,x₃)}

На рис. 4.3 изображены графы G₁ и G₂ и их композиции G₁(G₂). На этом же рисунке изображен граф G₂(G₁). Рекомендуется самостоятельно построить граф G₂(G₁) и убедиться, что графы G₁(G₂) и G₂(G₁) не изоморфны.

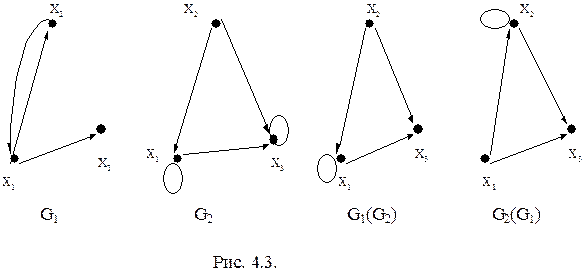
Пусть А₁ и A₂ – матрицы смежности вершин графов G₁(X,E₁) и G(X,E₂) соответственно. Рассмотрим матрицу A₁₂ элементы a_ij которой вычисляется так:

_n

a_ij = Úa_1ikÙa_2kj (4.1)

^k=1

где a_1ik и a_2kj – элементы матрицы смежности вершин первого и второго графов соответственно. Элемент a_ij равен 1, если в результирующем графе G₁(G₂) существует дуга, исходящая из вершины x_i и заходящая x_j, и нулю – в противном случае.

Пример 4.3. Выполнить операцию композиции для графов, пред­ставленных на рис. 4.3.

Составим матрицы смежности вершин графов:

			x1	x2	x3				x1	x2	x3
		x1						x1
A1	=	x2				A2	=	x2
		x3						x3

Вычислив элементы матрицы согласно (4.1), получаем:

			x1	x2	x3				x1	x2	x3
		x1						x1
A12	=	x2				A21	=	x2
		x3						x3

Нетрудно убедиться, что полученным матрицам смежности вершин соответствуют графы G₁(G₂) и G₂(G₁), представленные на рис. 4.3.

Декартово произведение графов. Пусть G₁(X,E₁) и G₂(Y,E₂) — два графа. Декартовым произведением G₁(X,E₁)´G₂(Y,E₂) графов G₁(X,E₁) и G₂(X,E₂) называется граф с множеством вершин X´Y, в котором дуга (ребро), идущая из вершины (x_iy_j) в (x_ky_l), существует тогда и только тогда когда существует дуга (x_ix_k), принадлежащая множеству дуг E₁ и j = l или когда существует дуга (y_j,y_l), принадлежащая множеству E₂ и i = k.

Выполнение операции декартова произведения рассмотрим на примере графов, изображенных на рис. 4.4. Множество вершин Z результирующего графа определяется как декартово произведение множеств X´Y. Множество Z содержит следующие элементы: z₁=(x₁y₁), z₂₌(x₁y₂), z₃=(x₁y₃), z₄=(x₂y₁), z₅=(x₂y₂), z₆=(x₂y₃).

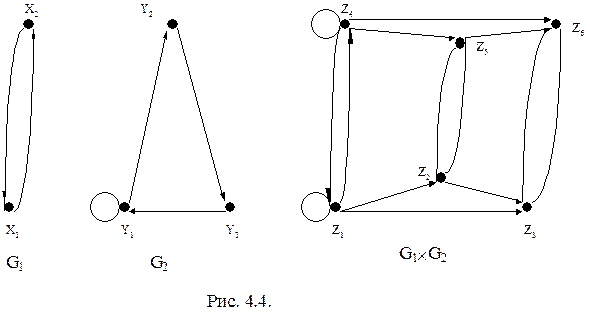Определим множество дуг результирующего графа. Для этого выделим группы вершин множества Z, компоненты которых совпадают. В рассматриваемом примере пять таких групп: две группы с совпадающими компонентами из множества X, и три группы, имеющие совпадающие компоненты из Y. Рассмотрим группу вершин результирующего графа, которые имеют общую компоненту x₁: z₁=(x₁y₁), z₂₌(x₁y₁), z₃=(x₁y₃). Согласно определению операции декартова произведения графов, множество дуг между этими вершинами определяется связями между вершинами множества Y. Таким образом, дуга (y₁,y₁) в графе G2 определяет наличие дуги (z₁,z₁) в результирующем графе. Для удобства рассмотрения всех дуг результирующего графа составим таблицу, в первом столбце которой перечисляются вершины с совпадающими компонентами, во втором – дуги между несовпадающими компонентами, а в третьем и четвертом – дуги в результирующем графе.

№ п.п.	Группы вершин с совпадаю­щими компонентами	Дуги для несовпада­­ю­щих компонент	Дуга (xiyj)®(xkyl)	Дуга (za,zb)
	z1=(x1y1), z2=(x1y2), z3=(x1y3)	(y1,y1) (y1,y2) (y2,y3) (y3,y1)	(x1y1)®(x1y1) (x1y1)®(x1y2) (x1y2)®(x1y3) (x1y3)®(x1y1)	(z1,z1) (z1,z2) (z2,z3) (z3,z1)
	z4=(x2y1), z5=(x2y2), z6=(x2y3)	(y1,y1) (y1,y2) (y2,y3) (y3,y1)	(x2y1)®(x2y1) (x2y1)®(x2y2) (x2y2)®(x2y3) (x2y3)®(x2y1)	(z4,z4) (z4,z5) (z5,z6) (z6,z4)
	z1=(x1y1), z4=(x2y1)	(x1,x2) (x2,x1)	(x1y1)®(x2y1) (x2y1)®(x1y1)	(z1,z4) (z4,z1)
	z2=(x1y2), z5=(x2y2)	(x1,x2) (x2,x1)	(x1y2)®(x2y2) (x1y2)®(x1y2)	(z2,z5) (z5,z2)
	Z3=(x1y3), z6=(x2y3)	(x1,x2) (x2,x1)	(x1y3)®(x2y3) (x2y3)®(x1y3)	(z3,z6) (z6,z3)

Граф G₁´ G₂ изображен на рис. 4.4.

Операция декартова произведения обладает следующими свойствами.

1. G₁´G₂ = G₂´G₁

2. G₁´(G₂´G₃) = (G₁´G₂)´G₃.

Операция декартова произведения графов может быть выполнена в матричной форме.

Пусть G₁(X,E₁) и G₂(Y,E₂) – два графа, имеющие n_x и n_y вершин соответственно. Результирующий граф G₁´G₂ имеет n_x×n_y вершин, а его матрица смежности вершин - квадратная матрица размером (n_x×n_y)´ (n_x ×n_y). Обозначим через a_ab = a_(ij)(kl) элемент матрицы смежности вершин, указывающий на наличие дуги (ребра), соединяющей вершину z_a=(x_iy_j) c z_b=(x_ky_l). Согласно определению операции этот элемент может быть вычислен при помощи матриц смежности вершин исходных графов следующим образом:

a_ab = a_(ij)(kl) = K_ik×a_2,jl Ú K_jl×a_1,ik, (4.2)

где a_1,ik, a_2,jl – элементы матрицы смежности вершин графов G₁ и G₂ соответственно;

K_ik – символ Кронекера, равный 1, если i=k, и нулю, если i¹k.

Пример 4.4. Выполнить операцию декартова произведения на графах, приведенных на рис. 4.4.

Составим матрицы смежности вершин исходных графов.

			x1	x2				y1	y2	y3
		x1					y1
A1	=	x2			A2	=	y2
							y3

Для построения матрицы смежности результирующего графа воспользуемся соотношением (4.2). В этом соотношении первое слагаемое K_ik×a_2,jl указывает на наличие дуг для вершин, у которых совпадают компоненты из множества X. Для пояснения сказанного, рассмотрим вспомогательную матрицу Axy, в которой элементы, для которых K_ik = 1, помечены символом X. Эти элементы принимают значения, равные значениям соответствующих элементов матрицы A₂ смежности вершин графа G₂, так, как это показано для матрицы A*.

			x1y1	x1y2	x1y3	x2y1	x2y2	x2y3
		x1y1	XÚY	X	X	Y	0	0
		x1y2	X	XÚY	X	0	Y	0
Axy	=	X1y3	X	X	XÚY	0	0	Y
		X2y1	Y	0	0	XÚY	X	X
		X2y2	0	Y	0	X	XÚY	X
		X2y3	0	0	Y	X	X	XÚY

			x1y1	x1y2	x1y3	x2y1	x2y2	x2y3
		x1y1	a1,11Ú a2,11	a2,12	a2,13	a1,12
		x1y2	a2,21	a1,11Úa2,22	a2,11		a1,12
A*	=	x1y3	a2,31	A2,32	a1,11Úa2,33	0	0	a1,12
		x2y1	a1,21	0	0	a1,22Úa2,11	a2,12	a2,13
		x2y2	0	a1,21	0	a2,21	a1,22Úa2,22	a2,23
		x2y3	0	0	a1,21	a2,31	a2,32	a1,22Ú a2,33

Второе слагаемое K_jl×a_1,ik соотношения (4.2) указывает на наличие дуг для групп вершин, у которых совпадают компоненты из множества Y. В матрице Axy элементы, для которых K_jl = 1 помечены символом Y. Эти элементы принимают значения, равные значениям соответствующих элементов матрицы A₁ смежности вершин графа G₁, так, как это показано для матрицы A*.

Заметим, что в матрицах Axy и A* на главной диагонали располагаются элементы, равные логической сумме значений элементов матриц смежности вершин обоих графов. Это определяется тем, что на главной диагонали расположены элементы, для которых K_ik = K_jl = 1.

Таким образом, матрица смежности вершин результирующего графа принимает вид:

			x1y1	x1y2	x1y3	x2y1	x2y2	x2y3
		x1y1
		x1y2
A	=	x1y3
		x2y1
		x2y2
		x2y3

Нетрудно убедиться, что полученной матрице смежности вершин соответствует граф G₁´G₂, представленный на рис. 4.4

Операция произведения графов. Пусть G₁(X,E₁) и G₂(Y,E₂) - два графа. Произведением G₁×G₂ графов G₁ и G₂ называется граф с множеством вершин X´Y, а дуга из вершины (x_i,y_j) в вершину (x_k,y_l) существует тогда и только тогда, когда существуют дуги (x_i,x_k) Î E₁ и (y_j,y_l) Î E₂.

Выполнение операции произведения рассмотрим на примере графов, изображенных на рис. 4.5. Множество вершин Z результирующего графа определяется как декартово произведение множеств X´Y. Множество Z содержит следующие элементы: z₁=(x₁y₁), z₂₌(x₁y₂), z₃=(x₁y₃), z₄=(x₂y₁), z₅=(x₂y₂), z₆=(x₂y₃).

Определим множество дуг результирующего графа. Для удобства рассмотрения составим таблицу, в первом столбце которой указываются дуги графа G₁, во втором – дуги графа G₂, а в третьем и четвертом – дуги результирующего графа.

G1	G2	(x1,y1)®(x2,y1)	(za, zb)
(x1,x2)	(y1,y1) (y1,y2) (y2,y3) (y3,y2)	(x1,y1)®(x2,y1) (x1,y1)®(x2,y2) (x1,y2)®(x2,y3) (x1,y3)®(x2,y2)	(z1,z4) (z1,z5) (z2,z6) (z3,z5)
(x2,x1)	(y1,y1) (y1,y2) (y2,y3) (y3,y2)	(x2,y1)®(x1,y1) (x2,y1)®(x1,y2) (x2,y2)®(x1,y3) (x2,y3)®(x1,y2)	(z4,z1) (z4,z2) (z5,z3) (z6,z2)

Результирующий граф G_1×G₂ изображен на рис.4.5.

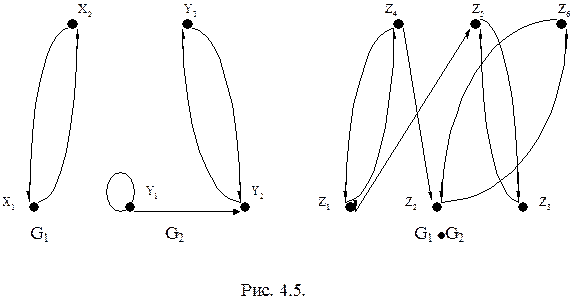
Операция произведения обладает следующими свойствами.

1. G₁×G₂ = G₂×G₁.

2. G₁×(G₂×G₃) = (G₁×G₂)×G₃.

Рассмотрим выполнение операции произведения графов в матричной форме.

Пусть G₁(X,E₁) и G₂(Y,E₂) – два графа, имеющие n_x и n_y вершин соответственно. Результирующий граф G₁×G₂ имеет n_x×n_y вершин, а его матрица смежности вершин - квадратная матрица размером (n_x×n_y)´ (n_x ×n_y). Обозначим через a_ab = a_(ij)(kl) элемент матрицы смежности вершин, указывающий на наличие дуги (ребра), соединяющей вершину z_a=(x_iy_j) c z_b=(x_ky_l). Этот элемент может быть вычислен при помощи матриц смежности вершин исходных графов следующим образом:

a_ab = a_(ij)(kl) = a_1,ik Ù a_2,jl, (4.3)

де a_1,ik, a_1,ik – элементы матрицы смежности вершин графов G₁ и G₂ соответственно.

Пример 4.5. Выполнить операцию произведения на графах, приведенных на рис. 4.5.

Составим матрицы смежности вершин исходных графов.

			x1	x2				y1	y2	y3
		x1					y1
A1	=	x2			A2	=	y2
							y3

Построим матрицу A смежности вершин результирующего графа, каждый элемент которой вычисляется согласно соотношению (4.3).

			x1y1	x1y2	x1y3	x2y1	x2y2	x2y3
		x1y1	a1,11Ù a2,11	a1,11Ùa2,12	a1,11Ù a2,13	a1,12Ùa2,11	a1,12Ù a2,12	a1,12Ù a2,13
		x1y2	a1,11Ù a2,21	a1,11Ù a2,22	a1,11Ù a2,23	a1,12Ù a2,21	a1,12Ù a2,22	a1,12Ù a2,23
A	=	x1y3	a1,11Ù a2,21	a1,11Ù a2,22	a1,11Ù a2,23	a1,12Ù a2,31	a1,12Ù a2,32	a1,12Ù a2,33
		x2y1	a1,21Ù a2,11	a1,21Ù a2,12	a1,21Ù a2,13	a1,22Ù a2,11	a1,22Ù a2,12	a1,22Ù a2,13
		x2y2	a1,21Ù a2,21	a1,21Ù a2,22	a1,21Ù a2,23	a1,12Ù a2,21	a1,12Ù a2,22	A1,12Ù a2,23
		x2y3	a1,21Ù a2,31	a1,21Ù a2,32	a1,21Ù a2,33	a1,22Ù a2,31	a1,12Ù a2,32	A1,12Ù a2,33

Для удобства рассмотрения разделим матрицу A на четыре квадратные подматрицы. Заметим, что каждая подматрица может быть получена путем логического элементов матрицы умножения A₂ на один из элементов a_1,ij матрицы A₁. С учетом этого матрицу A можно представить так:

			x1y1	x1y2	x1y3	x2y1	x2y2	x2y3
		x1y1	a1,11ÙA2	a1,12ÙA2
		x1y2
A	=	x1y3
		x2y1	a1,21ÙA2	a1,22ÙA2
		x2y2
		x2y3

Таким образом, матрица смежности вершин графа G₁×G₂ имеет вид:

			x1y1	x1y2	x1y3	x2y1	x2y2	x2y3
		x1y1
		x1y2
A	=	x1y3
		x2y1
		x2y2
		x2y3

Нетрудно убедиться, что полученной матрице смежности вершин соответствует граф G₁×G₂, представленный на рис. 4.5.

5. СВЯЗНЫЕ ГРАФЫ. КОМПОНЕНТА СВЯЗНОСТИ

Расcмотрим неориентированный граф G(X,E,F). Конечная последовательность ребер М = {e₁, e₂,..., e_k} графа называется цепью (маршрутом) длины k, если существует такая последовательность вершин (x₀, x₁,..., х_k), что F{e_i} = (x_i-1, x_i), где i = 1, 2,..., k. Вершины x₀ и x_k называются соответственно начальной и конечной вершинами маршрута, остальные вершины называются внутренними. Маршрут m длины k может записываться как в виде последовательности ребер m = {e₁, e₂,..., e_k}, так и в виде последовательности вершин m _{= {}x₀, x₁,..., x_k}.

Цепь m = {e₁, e₂,..., e_k}, в которой все ребра различны, называется простой. Цепь m ₌ {x₀, x₁,..., x_k}, в которой все вершины различны, называется элементарной.

Пусть m = {e₁, e₂,..., e_k} — цепь в графе G; для некоторой последовательности номеров i₁, i₂,..., i_r, (где r ³1, 1£ i₁<i₂<... <i_k) последовательность ребер (e_i1, e_i2,...,e_ir) называется подцепью цепи m; при этом говорят, что цепь (e_i1, e_i2,...,e_ir) выделена из цепи m = {e₁, e₂,..., e_k}.

Если цепь m имеет начальную вершину, но не имеет конечной, или имеет конечную вершину, но не имеет начальной, то она называется односторонне бесконечной. Если цепь не имеет ни начальной, ни конечной вершины, то она называется двусторонне бесконечной, замкнутой цепью, или циклом. Цепь называется нетривиальной, если она содержит хотя бы одно ребро (дугу); для обеспечения общности рассуждений вводится понятие нуль – цепи, не содержащей никаких ребер (дуг). Цикл называется простым, если все его ребра различны, и элементарным, если все вершины, через которые он проходит, различны.

Цепи m и m^| считаются равными, если они имеют одинаковую длину и состоят из одних и тех же ребер. В противном случае цепи m и m^| считаются различными.

Пример 5.1. В неориентированном графе G, приведенном на рис. 5.1 цепь m₁ = {e₁, e₂, e₄, e₈, e₁₀} длиной 5 может быть задана как последовательностью ребер, так и последовательностью вершин m₁ ={x₁, x₂, x₃, x₄, x₈, x₆}. В этой цепи вершина x₁ является начальной, а вершина x₆ — конечной. Последовательность ребер (e₂, e₄, e₈) — подцепь, выделенная из цепи m₁. Цепь m₂ = {e₁, e₂, e₄, e₇, e₅, e₄, e₇,e₃,...} является односторонне бесконечной.

Цепь m₃ = {e₄, e₈, e₁₀,e₉, e₆,e₇} является простой цепью, а m₄ = {e₂, e₄, e₈, e₁₀} — элементарной. Циклом является замкнутая цепь m₅ ={e₂, e₅, e₇, e₈, e₁₁, e₃}, а последовательность m₆ = {e₂, e₄, e₈, e₁₁, e₃} образует элементарный цикл.

Теорема 5.1. Пусть G = (X,E) - неориентированный граф, A(G) – матрица смежности его вершин. Тогда элемент c_ij матрицы C = Aⁿ(G) равен числу различных цепей длины n, соединяющих вершины x_i и x_j.

Доказательство. Если a_ik – число ребер, соединяющих вершины x_i и x_k, a_kj – число ребер, соединяющих вершины x_k и x_j, то произведение a_ik× a_kj есть число различных маршрутов длины 2, соединяющих вершины x_i и x_j и проходящих через вершину x_k. Тогда

,

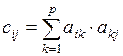где p – число вершин графа G, есть число всех маршрутов длины 2, соединяющих вершины x_i и x_j. С другой стороны, с_ij есть элемент матрицы A²(G), поэтому для n = 2 теорема доказана.

Воспользуемся индукцией по n и предположим, что теорема верна для m=n-1. Так как Aⁿ(G) = A(G)×A^n-1(G), то приведенные выше рассуждения доказывают справедливость теоремы для m = n. Тем самым теорема доказана.

Следствие 5.1. В неориентированном графе G маршрут длиной n существует тогда и только тогда, когда Aⁿ(G) ¹ 0.

Следствие 5.2. Если Aⁿ(G)=0 для некоторого n >0, то в неориен­ти­ро­ванном графе G нет циклов.

Пусть G(X,E) — неориентированный граф. Две вершины x_i и x_j называются связными, если существует маршрут m из вершины x_i в вершину x_j. Если маршрут m проходит через вершину x_k более одного раза, то можно, очевидно, удалить его циклический участок, и при этом оставшиеся ребра образуют маршрут m°, связывающий x_i и x_j. Отсюда следует, что связные вершины связаны элементарной цепью. Граф называется связным, если любая пара вершин связана, т.е. любые две вершины соединены цепью.

Пусть y - произвольная вершина неориентированного графа G = (X,E). Обо­значим через X_y множество всех вершин графа G, которые можно сое­динить с y цепями (вершину y также включаем в множество X_y). Пусть G_y — подграф графа G, множеством вершин которого является множество X_y, а множество ребер образуют все те ребра из E, концы которых принадлежат X_y. Построенный таким образом подграф G_y называется компонентой связности или связной компонентой графа G.

Теорема 5.2. Компоненты связности неориентированного графа G обладают следующими свойствами.

1. G_y ¹ 0 для любого y Î X.

2. Если G_y ¹ G_z, то G_y Ç G_z = Æ.

3. .

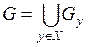Доказательство. Так как y Î X_y, то первое свойство выполняется. Вто­рое свойство докажем от противного. Если G_y Ç G_z ¹ Æ, то X_y Ç X_z ¹ Æ. Тогда существует вершина x Î X_y Ç X_z, которую можно соединить цепями как с y, так и с z. Отсюда следует, что вершины y и z можно соединить цепью, поэтому X_y = X_z. В результате получаем G_y = G_z, что и доказывает второе свойство.

Третье свойство следует из определения компоненты связности графа.

Следствие 5.3. Неориентированный граф связен тогда и только тогда, когда он состоит из одной компоненты связности.

Условия, эквивалентные связности графа, сформулированы в следую­щем утверждении.

Теорема 5.3. Неориентированный граф G = (X,E) связен тогда и только тогда, когда множество вершин X нельзя разбить на два непустых непересекающихся подмножества X₁ и X₂, которые не соединены ни одним ребром.

Доказательство. Необходимость указанного условия доказывается следующим образом. Если X₁ и X₂ — указанное в теореме разбиение, то любая цепь, соединяющая вершины x Î X₁ и y Î X₂, должна содержать хотя бы одно ребро, соединяющее множества X₁ и X₂. Поскольку таких ребер нет, то вершины x и y не могут быть соединены цепью. Это противоречит связности графа G, поэтому указанное разбиение не существует.

Доказательство достаточности следующее. Пусть G не связен, и пусть G_y – его компонента связности со множеством вершин X_y. Тогда X ¹ X_y, множество X₂ = X\X_y не пусто, X₂ Ç X_y = Æ. Ясно, что X₂ и X_y не соединены ни одним ребром. Это противоречит условию теоремы, поэтому граф G связен. Теорема доказана.

Следствие 5.4. Неориентированный граф G связен тогда и только тогда, когда не существует такой нумерации вершин графа G, при которой его матрица смежности вершин имеет вид

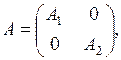
где A₁ и A₂ - квадратные матрицы.

Теорема 5.4. Пусть G – обыкновенный неориентированный граф с n вершинами и k компонентами связности. Тогда максимальное число ребер в графе G равно

.

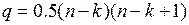Доказательство. Граф G имеет максимальное число ребер, если каждая компонента связности G_i, i = 1, 2,..., k имеет максимальное число ребер. Компонента связности G_i, имеющая максимальное число ребер, является полным графом. Число ребер полного графа с n_i вершинами равно 0,5×n_i×(n_i - 1). Таким образом, максимальное число ребер графа G, компоненты связности G_i которого имеют по n_i вершин, равно

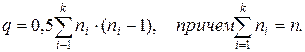
Полученное число зависит от того, как распределены вершины графа G по его компонентам связности. Предположим, что существует связные ком­поненты G₁ и G₂ графа G, имеющие более чем по одной вершине, т. е. n₁ > 1 и n₂ > 1. Пусть n₁ £ n₂. Рассмотрим граф G°, получаемый из графа G заменой компонент G₁ и G₂ на полные графы с (n₁-1) и (n₂+1) вершинами соответственно. Граф G° имеет n вершин и k компонент связности, а число его ребер равно

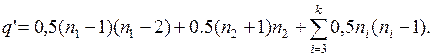
Тогда

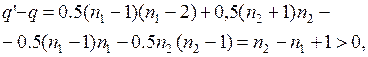
поэтому q’ > q. Итак, граф G° имеет больше ребер, чем граф G. Если и далее перестраивать граф указанным образом, то в результате получим граф, состоящий из k-1 изолированной вершины и одной полной компоненты связности с n - k + 1 вершиной. Этот граф имеет максимальное число ребер, равное 0,5×(n - k)×(n - k + 1). Теорема доказана.

Следствие 5.5. Если обыкновенный неориентированный граф G с n вершинами имеет больше, чем 0,5×(n - 1)×(n - 2) ребер, то он связен.

Доказательство. Из теоремы 5.3 следует, что 0,5×(n - 1)×(n - 2) — максимальное число ребер в обыкновенном графе с n вершинами и двумя компонентами связности. Если же в графе больше, чем 0,5×(n - 1)×(n - 2) ребер, то число компонент в нем либо k= 1, либо k ³ 3. Случай k ³ 3 противоречит условию, поэтому k = 1 и граф G связен.

Ориентированный граф G(X,E) называется сильно связным, если для любых его вершин x и y, x ¹ y, существуют пути m и m°, идущие соответственно из x в y и из y в x.

Рассмотрим теперь ориентированные графы. Пусть G(X,E,F) – орграф. Конечная последовательность дуг e₁, e₂, …, e_n графа G называется путем длиной n, или ориентированным маршрутом длины n, если существует такая последовательность вершин x₀, x₁, …, x_n, что F(e_i) = (x_i-1,x_i), где i = 1,2,…,. Путь m записывается в виде m = { e₁, e₂, …, e_n} или в виде m = {x₀, x₁, …, x_n }. В этом случае говорят, что путь состоит из дуг e₁, e₂, …, e_n, выходит из вершины x₀ и заходит в вершину x_n. Путь m называется простым, если все его дуги различны, и элементарным, если все его вершины различны.

Пути m и m’ считаются равными, если они имеют одинаковую длину и состоят из одних и тех же дуг. В противном случае пути m и m’ считаются различными.

Следующие утверждения доказываются точно так же, как это сделано для неориентированных графов в начале этого параграфа.

Теорема 5.5. Пусть G = (X,E) –орграф, A(G) – матрица смежности его вершин. Тогда элемент c_ij матрицы C = Aⁿ(G) равен числу различных путей длиной n, выходящих из вершины x_i и заходящих в вершину x_j.

Следствие 5.6. В орграфе G путь длиной n существует тогда и только тогда, когда Aⁿ(G) ¹ 0.

Следствие 5.7. Если Aⁿ(G)=0 для некоторого n >0, то в орграфе G нет циклов.

Орграф G(X,E) называется сильно связным, если для любых его вершин x и y, x¹y, существуют пути m и m’, идущие соответственно из x в y и из y в x.

Теорема 5.6. Орграф G(X,E) сильно связен тогда и только тогда, когда он имеет контур, проходящий через все вершины.

Доказательство. Пусть x и y – две вершины графа G, причем x ¹ y. По условию теоремы существует путь m₁, идущий из вершины x в вершину y.

Пусть X₁ – множество вершин пути m₁. Если X₁ = X, то достаточно взять путь m°, идущий из x в y и получим контур m₁ È m°, проходящий через все вершины графа. Если же X₁ ¹ X, то X\X₁ ¹ Æ. Тогда для вершины z Î X\X₁ строим путь m, идущий из y в z, и получаем путь m₂ = m₁ Èm. Пусть X₂ – множество вершин пути m₂. Тогда X₂ ¹ X₁, X₂ É X₁. Если продолжить этот процесс, то через конечное число шагов будет построен путь, содержащий все вершины графа, и, следовательно, искомый контур существует.

Пример сильно связного графа приведен на рис. 5.2.

6. ДЕРЕВЬЯ И ИХ СВОЙСТВА

В этом параграфе рассматривается частный вид графов, широко используемых, например, в теории электрических цепей, химии, вычислительной технике и в информатике.

Определение 6.1. Деревом называется связный граф, не содержащий цик­лов. Любой (в том числе несвязный) граф без циклов называется ацик­ли­ческим. Несвязный граф, каждая компонента связности которого является деревом, называется лесом. Можно сказать, что деревья являются компонентами леса. На рис. 6.1 изображены два дерева G ₁, G ₂ и лес G ₃.

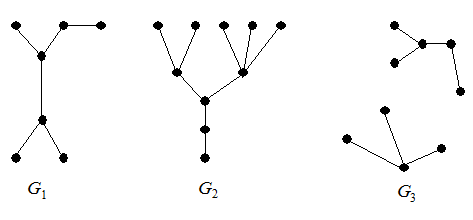
Рис. 6.1

Сформулируем основные свойства деревьев. Сделаем это в виде сово­куп­нос­ти утверждений, которые эквивалентны между собой (т.е. из любого утверждения следует любое другое) [].

Теорема 6.1. Пусть G (X, E) – неориентированный граф с p вершинами и q ребрами. Тогда следующие утверждения эквивалентны.

1°. G есть дерево.

2°. Любые две различные вершины x и y графа G соединены единственной простой цепью.

3°. G – связный граф, утрачивающий это свойство при удалении любого из его ребер.

4°. G – связный граф и p = q + 1.

5°. G – ациклический граф и p = q + 1.

6°. G – ациклический граф, причем если любые две его вершины x и y соединить ребром e, то в полученном графе будет ровно один простой цикл.

Для доказательства теоремы достаточно доказать следующую цепочку следствий: 1° Þ 2° Þ 3° Þ 4° Þ 5° Þ 6° Þ 1°, так как это означает, что из любого утверждения 1° – 6° выво­ди­тся любое другое.

1°Þ2°. Так как граф связен, то любые две его вершины можно сое­ди­нить простой цепью. Пусть m₁ и m₂ - две различные простые цепи, соединяю­щие вершины x и y. Если цепи m₁ и m₂ не имеют общих вершин, за исклю­чением вершин x и y, то 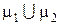есть простой цикл. Предположим, что цепи m₁ и m₂ имеют общие вершины, отличные от x и y. Пусть z – первая из таких вершин при движении от вершины x к вершине y и пусть m₁(x, z) и m₂(x, z) – части цепей m₁ и m₂, взятые от вершины x до вершины z. Тогда 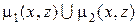- простой цикл. Это противоречит тому, что граф ацикличен, и поэтому m₁=m₂, т.е. утверждение 2° доказано.

2°Þ3°. Граф G – связен, поскольку любые две его различные вершины x и y соединены простой цепью. Возьмем некоторое ребро графа e = (x, y). Согласно 2° простая цепь m={ e } между вершинами x и y единственна. Если ребро e удалить, то вершины x и y будет невозможно соединить простой цепью, и полученный граф будет несвязным. Утверждение 3° доказано.

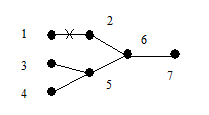
3°Þ4°. По условию 3° граф связен. Соотношение p = q + 1 докажем по индукции. Если граф имеет две вершины и удовлетворяет 3°, то он выглядит так:

В этом случае p = 2, q = 1 и соотношение p = q + 1 выполняется. Предполо­жим теперь, что соотношение верно для всех графов, удовлетворяющих 3° и имеющих меньше, чем p вершин, и докажем его для графа G с p вершинами. Удалим из графа G произвольное ребро e. Тогда новый граф G ´ будет несвязным и будет состоять из двух связных компонент G ₁ и G ₂. По предположению индукции имеем

p ₁ = q ₁ + 1, p ₂ = q ₂ + 1,

где p_i – число вершин компоненты G_i, q_i – число ее ребер. Следовательно,

p = p ₁ + p ₂, q = q ₁ + q ₂ + 1,

поэтому p = q ₁ + q ₂ + 2 = q + 1, и свойство 4° доказано.

4°Þ5°. Предположим, что граф G, удовлетворяющий 4°, имеет простой цикл m длиной l ³ 1. Этот цикл содержит l вершин и l ребер. Для любой из p - l вер­шин, не принадлежащих циклу m, существует инцидентное ей ребро, ле­жа­щее на кратчайшей цепи (т.е. цепи минимальной длины), идущей от данной вершины к некоторой вершине цикла m. Все такие ребра попарно различны. Если вершины x ₁ и x ₂ инцидентны одному такому ребру e, то e = (x ₁, x ₂), и кратчайшая цепь m₁ для вершины x ₁ проходит через вершину x ₂, а кратчайшая цепь m₂ для вершины x ₂ проходит через вершину x ₁ (рис. 6.2). Это противоречит тому, что цепи m₁ и m₂ – кратчайшие. Общее число ребер q в графе G в этом случае не меньше, чем l + p – l = p, т.е. q ³ p, что противоречит соотношению p = q + 1. Отсюда следует, что G – ациклический граф, и утверждение 5° доказано.

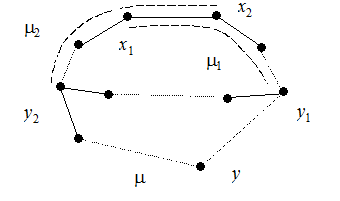
Рис. 6.2

5°Þ6°. Так как G – ациклический граф, то каждая его компонента связности G_i (i = 1, 2, …, k) является деревом. Для каждой компоненты G_i имеем в соответствии с 5° p_i = q_i + 1, откуда 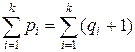, т.е. p = q + k. С другой стороны, p = q + 1, поэтому k = 1, т.е. граф G связен. Таким образом, G – дерево. Тогда (см. 2°) любые две различные вершины x и y графа G соединены единственной простой цепью. Если добавить ребро между несмежными вершинами x и y, то оно образует с указанной цепью единственный простой цикл. Утверждение 6° доказано.

6°Þ1°. По условию 6° G – ациклический граф. Если граф G не является связным, то возьмем вершины x и y из различных компонент связности графа G и соединим их ребром e. Построенный граф 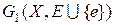является, как и граф G, ациклическим. Это противоречит свойству G, поэтому G – связный граф, и свойство 1° доказано. Таким образом, доказана и теорема 6.1.

Определение, аналогичное дереву, можно ввести и для орграфа.

Определение 6.2. Орграф G (X, E) называется прадеревом или ориентированным деревом, растущим из корня x ₀, при следующих условиях:

1°. Неориентированный граф G', соответствующий графу G, является деревом.

2°. Единственная простая цепь между x ₀ и любой другой вершиной x графа G' является путем в орграфе G, идущим из вершины x ₀ в вершину x.

На рис. 6.3 изображено ориентированное дерево.

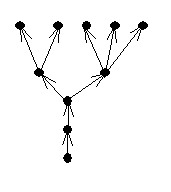
Рис. 6.3

В неориентированном графе G (X, E) вершина x называется концевой или висячей, если d(x) = 1, т.е. если этой вершине инцидентно единственное ребро e. Это ребро также называется концевым или висячим. С висячими вершинами связана следующая теорема.

Теорема 6.2. В любом дереве G (X, E) с p ³ 2 вершинами имеется не менее двух концевых вершин.

Доказательство. Пусть q – число ребер дерева G. В силу теоремы 6.1 p = q + 1. Кроме того, из теоремы 1.1 имеем

.

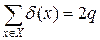Таким образом, получаем

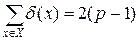. (6.1)

Предположим, что x ₀ – единственная концевая вершина в дереве G. Тогда d(x ₀) = 1, d(x) ³ 2, если x ¹ x ₀. Отсюда

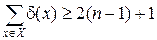. (6.2)

Неравенство (6.2) противоречит (6.1), поэтому либо концевых вершин нет, либо их по крайней мере две. Если концевых вершин в G нет, то d(x) ³ 2 для всех x Î X. Тогда

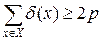. (6.3)

Неравенство (6.3) тоже противоречит (6.1). Отсюда следует, что концевых вершин в G две или больше. Теорема доказана.

Важным является вопрос о том, сколько существует деревьев с заданным числом вершин. Для деревьев с помеченными вершинами (например пронумерованными) или для помеченных деревьев ответ на этот вопрос дает следующая теорема.

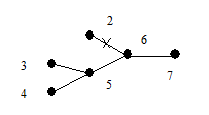
Теорема 6.3. (А. Кэли, 1897 г.). Число помеченных деревьев с p вершинами равно p^{p -2}.

Доказательство. Пусть G (X, E) – дерево с p помеченными вершинами. Для простоты предположим, что вершины пронумерованы в произвольном порядке числами 1, 2, …, p. Рассмотрим способ, позволяющий однозначно закодировать дерево G.

В соответствии с теоремой 6.2 дерево G имеет концевые вершины. Пусть x ₁ – первая концевая вершина в последовательности 1, 2, …, p и пусть e ₁ = (x ₁, y ₁) – соответствующее концевое ребро. Удалим из дерева вершину x ₁ и ребро e ₁. Получим новое дерево G ₁ с числом вершин p - 1. Найдем теперь пер­­вую концевую вершину x ₂ дерева G ₁ в последовательности вершин 1, 2, … …, p из множества {1, 2, …, p }\{ x ₁}, далее возьмем концевое ребро e ₂ = (x ₂, y ₂) и удалим из G ₁ x ₂ и e ₂. Эту процедуру последовательно повторяем. Через (p - 2) шага остается дерево из двух вершин x_{p -1}, y_{p -1} и одного ребра e_{p -1} = (x_{p -1}, y_{p -1}). Рассмотрим последовательность вершин

s(G) = { y ₁, y ₂, …, y_{p -2}}.

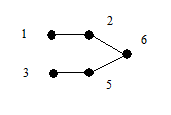
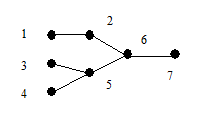
Очевидно, что по данному дереву последовательность строится однозначно. Покажем теперь, что по данной последовательности вершин s (G) дерево G можно восстановить однозначно. В последовательности 1, 2, …, p существуют вершины, не принадлежащие s (G). Выберем первую из них x ₁ и построим ребро e ₁ = (x ₁, y ₁). Затем удалим x ₁ из последовательности 1, 2, …, n и y ₁ удалим из s(G). Аналогичным образом построим ребро e ₂ = (x ₂, y ₂). Продолжая этот процесс, мы однозначно восстановим дерево G. Рассмотрим пример.

Построение кода	Восстановление
s(G)	s(G) и список вершин
(6,5,5,6) 2,3,4,5,6,7 (2,6)
(5,5,6) 3,4,5,6,7 (2,6,5)
(5,6) 4,5,6,7 (2,6,5,5)
(6) 5,6,7 (2,6,5,5,6)

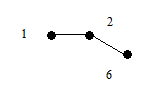
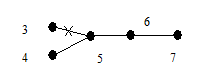
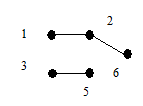
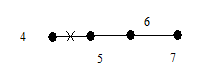
Рассмотренный пример позволяет отметить следующие две особеннос­ти:

1° В списке s(G) вершины могут повторяться.

2°. При восстановлении дерева последнее ребро соединяет вершину y_{p -2} и оставшуюся в списке 1, 2, …, p вершину не равную y_{p -2}.

Итак, существует взаимно однозначное соответствие между множеством помеченных деревьев с p вершинами и множеством последовательностей вершин s(G). Число таких последовательностей равно, очевидно, p^{p -2}, что и требовалось доказать.

Отметим, что среди p^{p -2} помеченных деревьев с p вершинами могут быть и изоморфные.

Определение 6.3. Подграф G ₁(X ₁, E ₁) неориентированного графа G (X, E) называется каркасом, или остовным деревом графа G, если G ₁ – дерево и X = X ₁.

Теорема 6.4. Граф G (X, E) тогда и только тогда обладает каркасом, когда он связен.

Доказательство. Необходимость этого очевидна. Докажем достаточность. Пусть G (X, E) – связный граф. Выясним, есть ли в графе G такое ребро, удаление которого не нарушает связности графа G. Если таких ребер нет, то граф есть дерево в соответствии с теоремой 1. Если же такое ребро, например e, существует, то выбросим его и придем к графу G ₁(X, E \{ e }). Затем указанную процедуру проделываем с графом G ₁ и т.д. Через конечное число шагов будет построен, очевидно, каркас графа G. Теорема доказана.

Доказательство теоремы дает алгоритм построения некоторого каркаса в связном графе. Однако связный граф может иметь несколько каркасов, поэтому естественно поставить задачу выбора каркаса, удовлетворяющего дополнительным условиям.

Определение 6.4. Графом с нагруженными ребрами (нагруженным графом) называется неориентированный граф G (X, E), каждому ребру e Î E которого поставлено в соответствие число m(e) ³ 0, называемое весом или длиной ребра e.

Аналогично можно определить нагруженный орграф.

Поставим задачу нахождения такого каркаса G ₁(X, E ₁) в нагруженном графе G (X, E), для которого сумма

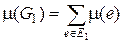
минимальна. Каркас с таким свойством называется минимальным каркасом. В соответствии с теоремой 4 каждый нагруженный связный граф обладает минимальным каркасом. Эта задача возникает при проектировании линий связи и электропередач, дорог, трубопроводов и т.п., когда требуется соединить системой каналов связи заданные узлы так, чтобы любые два узла были связаны (возможно, через другие узлы), а общая длина каналов связи была минимальной; при этом узлы можно считать вершинами нагруженного графа, весам ребер которого соответствует длина возможного канала связи между соответствующими узлами. Тогда искомая сеть каналов будет минимальным каркасом этого графа.

Дата добавления: 2014-01-06