Основные уравнения электродинамики

Тема 2.

Паразитические звуки

Позиционные изменения

1) Редукция. Изменение (ослабление) согласных и гласных звуков по
качеству и количеству (долготе) в зависимости от места в слове, нахождения
в безударных слогах, и т.д.

Рус. дом - дома - домоводство. В безударных слогах «о» подвергается редукции. Редукция может быть полной: Ваня - Вань, Иванович - Иваныч, Ивановна - Иванна.

Англ. пата - пате (второй гласный сначала редуцировался частично, а затем полностью, сохранившись в правописании). Good morning - g'morning -morning.

2) Апокопа - отпадение звука в конце слова: чтобы - чтоб.

3) Синкопа - отпадение звука не на конце слова: Иванович - Иваныч.

4) Оглушение - потеря звонкости имеет место во многих языках. Обыч­но это объясняется преждевременным возвращением голосовых связок в со­стояние покоя, напр., рус. луга - луг [лук], труба - труб [труп].

1) Протеза - появление звука в начале слова.

Например, рус. осемъ - восемь, ус(-енща) - гусеница, отчина - вотчина, исп. - estudiante от лат. studens, estrella от Stella (звезда), баш. ыстакан, ыштан (стакан, штаны).

2) Эпентеза - появление звука в середине слова.

Например, рус. Италия [Италийа] от Italia, Иоанн - Иван, в просторечии - кака-ва, рубель, шпиён, баш. итат. произношение «икс», «акт» как [икыс], [акыт].

3) Эпитеза - появление звука в конце слова: рус. песнь - песня.

4) Субституция. Замена звука, чуждого данному языку, звуком родного языка.

Например, нем. Herzog - герцог, Hitler - Гитлер (звука, соответствующего нем. «/г» нет в русском языке), анг. meeting - митинг (звук «ng» отсутствует в русском языке), вместо фр. звука, обозначаемого буквой u (tu, pure) и нем. ц в рус. яз. пишет­ся и произносится [йу].

5) Диэреза (греч. выкидка). Опущение звука: рус. солнце, сердце, честный, счастливый; баш. ултыр (садись) -утыр.

6) Элизия. Выпадение конечного гласного перед предшествующим глас­ным. Это явление особенно свойственно романским языкам, напр., фр. D'Artagnan - de Artagnan, DArc - de Arc), баш. ни эшлэй -нишлэй.

ВОПРОСЫ ДЛЯ САМОПРОВЕРКИ

1. Какие отношения существуют между парадигматикой и синтагматикой?

2. В чём выражается синтагматика фонем?

3. Какие видоизменения звуков происходят в потоке речи?

В обобщенном законе Гаусса свободный заряд Q, находящийся в объеме V, ограниченном замкнутой поверхностью S, определяется выражением . Применим к левой части теорему Остроградского-Гаусса. Получаем

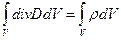(19) - III-е уравнение в интегральной форме

Это равенство справедливо для любого объема. Поэтому подынтегральные выражения равны, т.е.

(20) - III-е уравнение в дифференциальной форме

Уравнение (20), справедливое в любой обыкновенной точке пространства в любой момент времени, выражает обобщенный закон Гаусса в дифференциальной форме. Оно математически выражает физический факт: источником или стоком векторного поля D является плотность объемного электрического заряда, линии вектора D начинаются в точках, где > 0 и заканчиваются в точках, где < 0. Уравнение называют третьим уравнением Максвелла в дифференциальной форме, а обобщенный закон Гаусса является его интегральной формой.

Применяя к принципу непрерывности магнитного потока теорему Остроградского-Гаусса, получаем:

(21) - IV-е уравнение в интегральной форме

Поскольку объем V произволен, то равенство может выполняться только при

(22) - IV-е уравнение в дифференциальной форме

Это уравнение, справедливое в любой обыкновенной точке пространства в любой момент времени, выражает в дифференциальной форме физический факт непрерывности векторных линий магнитной индукции; векторное поле магнитной индукции В не имеет истоков; в природе магнитные заряды отсутствуют. Уравнение (22) называют четвертым уравнением Максвелла в дифференциальной форме, а принцип непрерывности магнитного потока является его интегральной формой.

Рассмотрим закон полного тока . Он справедлив для любого вещества, но при постоянном во времени токе. Применим к левой части закона полного тока теорему Стокса. Получаем

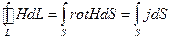(23)

Поскольку поверхность S произвольна, но одна и та же в поверхностных интегралах, то подынтегральные выражения поверхностных интегралов равны, т.е.

rotH = j(p) (24)

Это дифференциальная форма закона полного тока в стационарном случае. Действительно, применим к обеим частям уравнения операцию дивергенции. Дивергенция ротора любого вектора всегда равна нулю. Поэтому 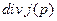= 0, т.е. получено уравнение, но справедливое только для случая постоянного тока (и заряда), когда = 0.

Пусть плотность тока зависит от времени, т.е. 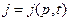. Если применить выражение к нестационарному полю, то оно оказывается несправедливым, поскольку не удовлетворяется закон сохранения электрического заряда. Это указывает на то, что эти выражения являются неполными. Допустим, что дополнено некоторым слагаемым . Применив здесь операцию дивергенции к обеим частям равенства, с учетом получаем .

Используя закон сохранения электрического заряда и учитывая, имеем . Решением последнего уравнения 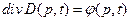является , где a — произвольный вектор. Максвелл постулировал, что 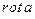= 0, тогда 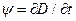. Вектор 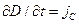называют плотностью тока смещения. При этом имеем

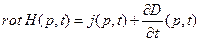(25)

Здесь сумма j + j_c называется вектором плотности полного электрического тока. Интегральной формой уравнения является:

(26) - I-е уравнение в интегральной форме

Это закон полного тока в интегральной форме, справедливый в нестационарном случае.

Уравнение (25) выражает закон полного тока в дифференциальной форме. Оно устанавливает количественную связь между входящими в него векторными величинами в любой точке пространства и в любой момент времени. Изменяющаяся в момент времени t в точке пространства р плотность тока 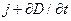порождает в этой точке и в этот момент времени вихрь вектора Н. Если даже в точке р в момент времени t плотность тока j отсутствует, то вихрь меняющегося в пространстве магнитного поля порождается током смещения с плотностью , т.е. меняющимся во времени электрическим полем. Уравнение (25) называют первым уравнением Максвелла.

Пусть имеется поверхность S, опирающаяся на контур L (рис. 1). Поместим контур L во внешнее магнитное поле с индукцией В. Изменение во времени магнитного потока Ф через поверхность S, вызывает в этом контуре электродвижущую силу Э (э.д.с.), определяемую циркуляцией вектора Е вдоль контура L: 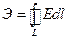. Если контур L имеет некоторую проводимость, то под действием э.д.с. в контуре возникает ток проводимости, который можно измерить. Опыт показывает, что величина э.д.с. равна скорости изменения магнитного потока Ф во времени: 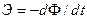, т.е.

(27)

Это закон электромагнитной индукции, открытый Фарадеем опытным путем.

Максвелл обобщил закон электромагнитной индукции, постулировав равенство для произвольного замкнутого контура, проходящего в любой среде. В частном случае контур L может быть проводящим, он может быть и воображаемым. С учетом этого постулата называют обобщенным законом электромагнитной индукции.

В электродинамике неподвижных сред контур L должен быть покоящимся (неподвижным). Поверхность S тоже считаем неподвижной, но произвольной. Тогда изменение магнитного потока во времени происходит только за счет изменения вектора В во времени. Это значит, что производную по времени можно внести под знак интеграла, где интегрирование выполняется по пространственным координатам, в виде частной производной. При этом получаем:

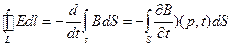(28)=2-е уравнение в интегральной форме

Из этого обобщенного закона электромагнитной индукции для неподвижных сред получают второе уравнение Максвелла.

Применим к левой части (28) теорему Стокса. Получаем:

Так как поверхность S произвольна, то это равенство возможно только при равенстве подынтегральных выражений, т.е.

(29) - II-е уравнение Максвелла в дифференциальной форме

Это второе уравнение Максвелла. Оно справедливо в любой точке пространства в любой момент времени и выражает обобщенный закон электромагнитной индукции в дифференциальной форме. Из (29) следует, что изменение во времени в точке р магнитного поля сопровождается изменением в окрестности точки р (по пространственным координатам) электрического поля.

Выражение (29) является интегральной формой второго уравнения Максвелла.

Полная система уравнений Максвелла состоит из четырех уравнений

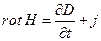
(30)

Первые два уравнения обладают симметрией в следующем смысле: по первому уравнению изменение во времени электрической индукции порождает вихревое магнитное поле, вектор напряженности которого изменяется в пространстве; по второму уравнению изменение во времени магнитной индукции порождает вихревое электрическое поле, изменяющееся в пространстве. Из этого следует возможность существования ЭМ волн в средах вдали от тел с токами проводимости. Электрическое и магнитное поля могут существовать, взаимно порождая друг друга.

По аналогии с первым уравнением Максвелла величину ЭВ 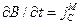в правой части второго уравнения Максвелла можно рассматривать как плотность магнитного тока смещения.

Система уравнений Максвелла — это результат обобщения основных законов электродинамики, установленных с помощью опытных данных. Эти уравнения правильно отражают законы электромагнетизма, так как выводы теории полностью подтверждаются опытными данными. Не обнаружено опытных данных, противоречащих теоретическим результатам, найденным на основе решения системы уравнений Максвелла. Поэтому система уравнений Максвелла принимается в качестве аксиом.

Дата добавления: 2014-01-06