
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Теорема Чебышева и ее следствия
Теорема Чебышева. Пусть дисперсии независимых СВ Х1,Х2,…,Хn ограничены одной и той же постоянной С, а число их достаточно велико. Тогда, как бы мало не было число ε >0,вероятность того, что отклонение среднего арифметического этих СВ от среднего арифметического их математических ожиданий не превзойдет ε по абсолютной величине, сколь угодно близка к единице.
Следствие1. Если независимые СВ имеют одинаковые математические ожидания, равные а, дисперсии их ограничены одной и той же постоянной С, а число их достаточно велико, то для любого ε >0 вероятность того, что отклонение среднего арифметического этих СВ от а не превзойдет по абсолютной величине ε,сколь угодно близка к единице:
Р (| Х1+Х2+…Хn / n –а |≤ ε)>1-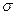 , как бы ни были малы ε и
, как бы ни были малы ε и 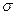 .Следствие 1 является наиболее простой формой закона больших чисел. Согласно закону больших чисел, среднее арифметическое достаточно большого числа измерений практически будет, как угодно мало отличаться от истинного значения математического ожидания искомой величины.
.Следствие 1 является наиболее простой формой закона больших чисел. Согласно закону больших чисел, среднее арифметическое достаточно большого числа измерений практически будет, как угодно мало отличаться от истинного значения математического ожидания искомой величины.
Следствие 2. (теорема Пуассона). Если вероятность pi наступления события А в i-испытании (i=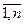 ) не меняется, когда становятся известными исходы предыдущих испытаний, а число испытаний n достаточно велико, то вероятность того, что частность события А будет как угодно мало отличаться от среднего арифметического вероятностей pi, сколь угодно близка к единице:
) не меняется, когда становятся известными исходы предыдущих испытаний, а число испытаний n достаточно велико, то вероятность того, что частность события А будет как угодно мало отличаться от среднего арифметического вероятностей pi, сколь угодно близка к единице:
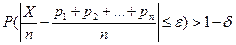 , для любых ε >0 и
, для любых ε >0 и 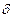 >0
>0
Следствие3 (теорема Бернулли). Если вероятность р наступления события А в каждом из n независимых испытаний постоянна, а число испытаний достаточно велико, то вероятность того, что частость события А будет как угодно мало отличаться от его вероятности, сколь угодно близка к единице:
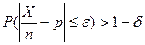
Ни одна из рассмотренных теорем не дает точного или хотя бы приближенного значения искомой вероятности, а указывается лишь ее нижняя или верхняя граница. Приближенные значения вероятностей при больших n можно получить только с помощью предельных теорем. В них на случайные величины налагаются дополнительные ограничения или рассматриваются СВ определенного вида.
Теорема (Ляпунова). Если независимые СВ Х1,Х2,…,Хn имеют конечные математические ожидания а1,а2,…,аn и конечные дисперсии, число их достаточно велико, а предел
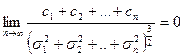 (*)
(*)
где Сi-абсолютные центральные моменты 3-го порядка СВ Хi (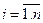 ),то сумма их с достаточной степенью точности распределены по нормальному закону с параметрами:
),то сумма их с достаточной степенью точности распределены по нормальному закону с параметрами:
а=а1+а2+…+аn; 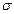 2=
2=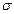 12+
12+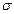 22+…+
22+…+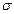 n2.
n2.
Условие (*) называется условием Ляпунова. Смысл его состоит в том, что действие каждого слагаемого невелико по сравнению с суммарным действием их всех.
Теорема. Сумма достаточно большого числа одинаково распределенных независимых СВ, имеющих абсолютные центральные моменты 3-го порядка, распределена по нормальному закону.
Вопросы для самоконтроля знаний:
1.Алгебра событий.
2.Условная вероятность. Независимые случайные события.
3. Классическое определение вероятности события
4. Формула Бернулли, Пуассона, Теорема Лапласа (практическая значимость)
5. Формула полной вероятности, формула Байеса (практическая значимость)
6.Как определить математическое ожидание и дисперсию дискретной случайной величины?
7. Сущность закона больших чисел.
8. Как определить математическое ожидание и дисперсию непрерывной случайной величины.
|
|
Дата добавления: 2014-01-06; Просмотров: 3459; Нарушение авторских прав?; Мы поможем в написании вашей работы!