
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Оценка точности выполнения арифметических операций
|
|
|
|
Как уже неоднократно отмечалось, для представления чисел в любой форме в компьютере отводится конечная длина разрядной сетки. Поэтому числа, в общем случае, из-за неизбежных процедур округления, представляются с некоторой погрешностью. В связи с этим вычисления в компьютере выполня-ются с погрешностью, которая в некоторых случаях может существенно накапливаться.
Пусть величины А и В заданы с абсолютными погрешностями А и В:
А = [A] А, В = [B] В= где [A] и [B] - машинное представление чисел А и В. Тогда, как нам уже известно, относительные погрешности представления этих чисел будут равны:
A = A / |A| и B = B / |B|.
Можно показать, что относительная погрешность алгебраической суммы будет равна:
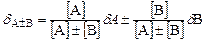 ,
,
относительная погрешность произведения:
AB = |A| + |B|,
а относительная погрешность частного:
A/B = |A| + |B|,
Из приведенных соотношений видно, что операция умножения и деления незначительно увеличивают относительную погрешность, а вычитание почти равных чисел может сильно ее увеличить. Действительно, если принять, что
= A B, а [A] мало отличается от [B], то

В связи с тем, что величина (А - В) в данном случае мала, а то А-В может быть достаточно большой величиной.
Из-за неизбежных погрешностей машинных вычислений может наблюдаться нарушение некоторых основных законов математики. Например, может не выполняться точно закон ассоциативности для умножения. Закон дистрибутивности, связывающий операции умножения и сложения, может значительно нарушаться, т.е. не будет строго выполняться равенство:
А х (В + С) = (А х В) + (А х С),
а отсюда может возникнуть ситуация, когда
2 х (А2+ В2) < (А + В)2.
Поэтому нужно очень тщательно оценивать конкретные условия вычислений и, при необходимости, переходить к представлению чисел с двойной точностью и принимать различные другие меры, чтобы в какой-то степени исключить влияние накопленной погрешности на результат вычислений.
|
|
|
|
Дата добавления: 2014-01-06; Просмотров: 358; Нарушение авторских прав?; Мы поможем в написании вашей работы!