
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Лекция 15. Взаимодействие электромагнитных волн с веществом. Фазовая и групповая скорости электромагнитных волн. Нормальная и аномальная дисперсии. Электронная теория дисперсии
|
|
|
|
Лекция 13. Обобщение Максвеллом представлений об электромагнитной индукции. Взаимосвязь переменных электрического и магнитного полей. Уравнения Максвелла в интегральной и дифференциальной формах, их физическое истолкование Сравнительная характеристика электрического и магнитного полей.
Про классическую теорию электромагнитного взаимодействия и его переносчика - электромагнитное поле - говорят иногда, что электродинамика Максвелла - это уравнения Максвелла. В 60 - ых годах прошлого столетия Максвелл выполнил работу, подобную той, которую два века до него осуществил Ньютон. Если Ньютон довершил создание первой фундаментальной теории движения, то Максвелл завершил создание первой теории физического взаимодействия (электромагнитного). Подобно классической механике Ньютона, в основу электродинамики Максвелла также были положены некоторые предельно фундаментальные и элементарные соотношения, выраженные уравнениями, получившими имя Максвелла.
Эти уравнения имеют две формы - интегральную и дифференциальную своего выражения и фактически они выражают взаимосвязь характеристик электромагнитного поля с характеристиками источников (зарядов и токов), это поле порождающих. Эта связь не имеет такого простого выражения, как, например связь мер движения и взаимодействия, выражаемая основным законом динамики - вторым законом Ньютона. Поэтому уравнения Максвелла, выражающие основную идею электродинамики - учения об электромагнитном взаимодействии - появляются при её изучении в вузе - лишь в конце курса.
Как и любые другие предельно общие теоретические положения, уравнения Максвелла в рамках самой электродинамики формально не выводятся. Они получаются как результат творческого обобщения разнообразного опытно-экспериментального материала, и их правильность подтверждается различными следствиями и практическими приложениями.
|
|
|
До Максвелла была известна полная система уравнений электро- и магнито статики и одно уравнение электро динамики - уравнение, выражающее закон электромагнитной индукции. В целом же эта совокупность уравнений не являлась полной системой, однозначно задающей состояние электромагнитного поля. Для получения такой системы Максвелл произвёл обобщение закона электромагнитной индукции e = - dФ¤dt, записав его уравнение в интегральной форме:
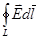 = -
= - = -
= - (вектор
(вектор 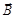 зависит и от t, и от
зависит и от t, и от 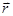 , а поток Ф =
, а поток Ф = 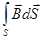 - только от t)
- только от t)
Полученное уравнение можно представлять себе как обобщённую на вихревое электрическое поле, теорему о циркуляции вектора  в электростатике. Здесь Максвелл фактически выбросил проводящий контур, который был у Фарадея и который, по Максвеллу, являлся просто индикатором наличия (по индукционным токам) вихревого электрического поля в области вокруг изменяющегося магнитного поля.
в электростатике. Здесь Максвелл фактически выбросил проводящий контур, который был у Фарадея и который, по Максвеллу, являлся просто индикатором наличия (по индукционным токам) вихревого электрического поля в области вокруг изменяющегося магнитного поля.
В представленной Максвеллом форме закона электромагнитной индукции более выпукло просвечивает физическая суть явления, согласно которому переменное магнитное поле порождает в окружающем пространстве вихревое (с ненулевой циркуляцией) электрическое поле. Представив так явление электромагнитной индукции, Максвелл смог, оперевшись на соображения симметрии, предположить возможность существования в природе и обратного электромагнитной индукции эффекта. Его можно назвать магнитоэлектрической индукцией, суть которой в том, что изменяющееся во времени электрическое поле, порождает в окружающем пространстве магнитное поле. Формально это записывается так, что циркуляция напряженности магнитного поля равна быстроте изменения во времени потока индукции электрического поля. С учётом же того, что магнитное поле с самого начала (со статического состояния) является вихревым, то есть для него циркуляция всегда не равна нулю, обобщённая взаимосвязь магнитного и электрического полей примет вид:
|
|
|
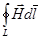 = I + Iсм, где Iсм =
= I + Iсм, где Iсм = 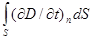
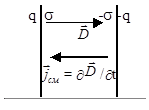 Здесь быстрота изменения потока индукции электрического поля формально эквивалентна некоторому току. Этот ток называют током смещения. Можно представить, что этот ток как бы замыкает протекание тока в цепи, например, с конденсаторами, через которые обычный ток проводимости не протекает. Плотность тока смещения
Здесь быстрота изменения потока индукции электрического поля формально эквивалентна некоторому току. Этот ток называют током смещения. Можно представить, что этот ток как бы замыкает протекание тока в цепи, например, с конденсаторами, через которые обычный ток проводимости не протекает. Плотность тока смещения  равна быстроте изменения электрического смещения (вектора
равна быстроте изменения электрического смещения (вектора  ):
):  = (¶
= (¶ /¶t). При разряде заряженного конденсатора по проводам протекает ток проводимости, и, кроме того, в пространстве между пластинами убывает (изменяется) электрическое поле.
/¶t). При разряде заряженного конденсатора по проводам протекает ток проводимости, и, кроме того, в пространстве между пластинами убывает (изменяется) электрическое поле.
Быстрота же изменения индукции электрического поля, то есть ¶ ¤¶t и есть плотность тока смещения
¤¶t и есть плотность тока смещения  . Ток смещения замыкает ток проводимости в разрывах между проводниками. Он, как и ток проводимости, создаёт вокруг себя магнитное поле, а в диэлектрике (там его называют поляризационным током) он выделяет тепло - так называемые диэлектрические потери.
. Ток смещения замыкает ток проводимости в разрывах между проводниками. Он, как и ток проводимости, создаёт вокруг себя магнитное поле, а в диэлектрике (там его называют поляризационным током) он выделяет тепло - так называемые диэлектрические потери.
Итак, теперь мы можем записать полную систему уравнений единого электромагнитного поля - систему уравнений Максвелла:
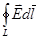 = -
= - 
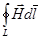 = I +
= I + 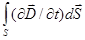
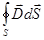 = qå
= qå 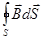 = 0
= 0
В статическом состоянии электрическое (электростатическое) поле порождается только неподвижными (или равномерно движущимися) в данной ИСО электрическими зарядами и является потенциальным (обладает нулевой циркуляцией). Магнитостатическое поле порождается только токами и всегда является непотенциальным (вихревым). Электростатическое поле, имея своими источниками заряды, имеет начало своих силовых линий на положительных зарядах и конец - на отрицательных зарядах (или в бесконечности). Магнитное же поле не имеет таких источников, поскольку магнитных монополей до сих пор не обнаружено, и потому его силовые линии даже в статическом состоянии являются замкнутыми, не имея ни начала, ни конца.
В динамическом же, нестационарном состоянии, когда источники полей и сами, порождаемые ими поля, становятся изменяющимися во времени, выявляется новая принципиальная особенность электрического и магнитного нестационарных полей. Выясняется, что в этом состоянии они приобретают способность порождать друг друга, становиться источниками друг друга. В результате возникает новое неразрывно взаимосвязанное состояние единого электромагнитного поля. Первое уравнение Максвелла, как уже говорилось, указывает на то, что изменяющееся во времени магнитное поле, порождает в окружающем пространстве вихревое электрическое поле. Второе же уравнение Максвелла говорит о том, что магнитное поле порождается не только токами, но и переменным во времени электрическим полем. В итоге мы можем заключить, что переменные (нестационарные) электрическое и магнитное поля являются взаимными источниками друг друга, и их различие во многом относительно. В нестационарном состоянии они способны существовать совершенно самостоятельно от источников (переменных токов), их породивших, в виде единого неразрывного электромагнитного поля.
|
|
|
Последние два уравнения Максвелла указывают на разный характер симметрии электрического и магнитного стационарных полей.
Для решения основной задачи электродинамики, уравнения Максвелла, выражающие её основную идею (связь характеристик поля с характеристиками его источников), должны быть дополнены так называемыми материальными уравнениями, связывающими характеристики поля с характеристиками вещественной среды. Этими уравнениями являются следующие:
 = eоe
= eоe ;
; 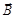 = mоm
= mоm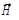 и
и 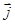 = g
= g , где e и m - диэлектрическая и магнитная проницаемости среды, а g - удельная электропроводность среды.
, где e и m - диэлектрическая и магнитная проницаемости среды, а g - удельная электропроводность среды.
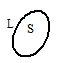 Уравнения Максвелла часто записывают в более компактной - дифференциальной форме, которая получается из интегральной формы путём предельного перехода контуров и поверхностей интегрирования к нулю: S ® 0 и L ® 0.
Уравнения Максвелла часто записывают в более компактной - дифференциальной форме, которая получается из интегральной формы путём предельного перехода контуров и поверхностей интегрирования к нулю: S ® 0 и L ® 0.
Введем векторный оператор, называемый "набла" и обозначаемый Ñ, как вектор со следующими компонентами: Ñ = (¶/¶х, ¶/¶у, ¶/¶z).
Для любого векторного поля  (
(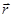 ) = (Ах, Ау, Аz) важными являются следующие совокупности дифференциальных операций:
) = (Ах, Ау, Аz) важными являются следующие совокупности дифференциальных операций:
|
|
|
а) скалярная, называемая дивергенцией  :Ñ
:Ñ = diu
= diu  = ¶Ах/¶х + ¶Ау/¶у + ¶Аz/¶z
= ¶Ах/¶х + ¶Ау/¶у + ¶Аz/¶z
б) векторная, называемая ротором  :
:
Ñ  = rot
= rot  =
= 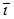 (¶Ау/¶z - ¶Ая/¶у) +
(¶Ау/¶z - ¶Ая/¶у) +  (¶Аz/¶х - ¶Ах/¶z) +
(¶Аz/¶х - ¶Ах/¶z) + 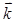 (¶Ау/¶Х - ¶АХ/¶У)
(¶Ау/¶Х - ¶АХ/¶У)
В этих обозначениях уравнения Максвелла в дифференциальной форме, примут следующий вид:
rot = - ¶
= - ¶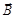 /¶t; rot
/¶t; rot 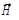 =
= 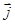 + ¶
+ ¶ /¶t; diu
/¶t; diu  = r; diu
= r; diu 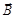 = 0
= 0
или Ñ  = - ¶
= - ¶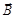 /¶t; Ñ
/¶t; Ñ 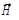 =
= 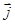 + ¶
+ ¶ /¶t; Ñ
/¶t; Ñ  = r; Ñ
= r; Ñ 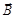 = 0
= 0
В уравнения Максвелла входят только свободные заряды r и токи проводимости 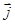 . Связанные заряды и молекулярные токи входят в эти уравнения неявно - через характеристики среды – диэлектрическую и магнитную проницаемости e и m.
. Связанные заряды и молекулярные токи входят в эти уравнения неявно - через характеристики среды – диэлектрическую и магнитную проницаемости e и m.
Для перехода к дифференциальной форме записи теоремы о циркуляции воспользуемся известной из векторного анализа теоремой Стокса, связывающей циркуляцию вектора с поверхностным интегралом от ротора этого вектора:
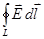 =
=  ,
,
гдеS – поверхность, ограниченная контуром L. Под ротором вектора понимают векторный дифференциальный оператор, задаваемый следующим образом:
rot  =
= 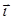 (¶Еу/¶z - ¶Еz/¶у) +
(¶Еу/¶z - ¶Еz/¶у) + 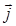 ( ¶Еz/¶х - ¶Ех/¶z) +
( ¶Еz/¶х - ¶Ех/¶z) + 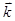 (¶Еx/¶y - ¶Еy/¶x)
(¶Еx/¶y - ¶Еy/¶x)
Физический смысл ротора вскрывают, устремляя поверхность S к нулю. В пределах достаточно малой поверхности ротор вектора можно считать постоянным и вынести за знак интеграла:
 = rot
= rot ×
× 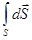 = rot
= rot ×S.
×S.
Тогда, согласно теореме Стокса:rot  = (1/S)
= (1/S)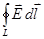 при S ® 0.
при S ® 0.
Отсюда ротор вектора можно определить как поверхностную плотность циркуляции этого вектора.
Так как в ЭСП циркуляция вектора  равна нулю, то равен нулю и ротор вектора
равна нулю, то равен нулю и ротор вектора  :
:
rot  = 0.
= 0.
Это уравнение и есть дифференциальная форма теоремы о циркуляции вектора  в ЭСП.
в ЭСП.
Для перехода к дифференциальной форме записи теоремы Остроградского – Гаусса воспользуемся известной из векторного анализа теоремой Гаусса, связывающей поток вектора по замкнутой поверхности с интегралом от дивергенции этого вектора по объему, заключенному в этой поверхности:
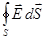 =
= 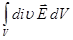
Под дивергенцией вектора понимают скалярный дифференциальный оператор (совокупность производных), задаваемый следующим образом:
div  = ¶Ех/¶х + ¶Еу/¶у + ¶Еz/¶z.
= ¶Ех/¶х + ¶Еу/¶у + ¶Еz/¶z.
Физический смысл дивергенции вскрывают, устремляя объем V к нулю. В пределах достаточно малого объема дивергенцию вектора можно считать постоянной и вынести за знак интеграла:
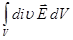 = div
= div ×
×  = (1/V) div
= (1/V) div  . Тогда, согласно теореме Гаусса,
. Тогда, согласно теореме Гаусса,
div  = (1/V)
= (1/V)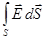 при V ® 0.
при V ® 0.
Отсюда дивергенцию вектора можно определить как объемную плотность потока этого вектора.
Соотнося теорему Остроградского – Гаусса 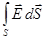 = qå/eо = (1/eо)
= qå/eо = (1/eо) и теорему Гаусса
и теорему Гаусса 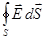 =
= 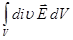 , видим, что левые их части равны друг другу. Приравнивая их правые части, получаем:
, видим, что левые их части равны друг другу. Приравнивая их правые части, получаем:
div  = r/eо.
= r/eо.
Это уравнение и представляет собой дифференциальную форму теоремы Остроградского – Гаусса.
Лекция 14. Электромагнитные волны. Объяснение возникновения электромагнитных волн с позиций уравнений Максвелла. Уравнение бегущей электромагнитной волны. Волновое уравнение. Перенос энергии электромагнитной волной. Вектор Умова - Пойнтинга. Излучение диполя.
Электромагнитные волны представляют собой распространяющиеся в пространстве взаимосвязанные колебания электрического и магнитного полей. В отличие от звуковых (акустических) волн, электромагнитные волны могут распространяться в вакууме.
Качественно механизм возникновения свободного (от источников в виде электрических зарядов и токов) электромагнитного поля может быть пояснён на основе анализа физической сущности уравнений Максвелла. Два фундаментальных эффекта, отображаемых уравнениями Максвелла - электромагнитная индукция (порождение переменным магнитным полем переменного вихревого электрического поля) и магнитоэлектрическая индукция (порождение переменным электрическим полем переменного магнитного поля) приводят к возможности электрического и магнитного переменных полей быть взаимными источниками друг друга. Взаимосвязанное изменение электрического и магнитного полей и представляет собой единое электромагнитное поле, которое способно в вакууме распространяться со скоростью света
с = 3×108 м/с. Это поле, способное существовать совершенно независимо от зарядов и токов и вообще от вещества и представляет собой второй (наряду с веществом) - полевой вид (форму) существования материи.
В опыте электромагнитные волны были обнаружены в 1886 г Г. Герцем, спустя 10 лет после смерти, предсказавшего теоретически их существование Максвелла. Из уравнений Максвелла в непроводящей среде, где r = 0 и 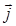 = 0, взяв операцию ротора от первого уравнения и подставив в него выражение для rot
= 0, взяв операцию ротора от первого уравнения и подставив в него выражение для rot 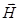 из второго уравнения, получим:
из второго уравнения, получим:
rot = - ¶
= - ¶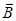 /¶t = - mоm¶
/¶t = - mоm¶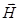 /¶t; rot rot
/¶t; rot rot = -mоm¶/¶t(rot
= -mоm¶/¶t(rot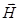 ) = - mоmeоe¶
) = - mоmeоe¶ 2/¶t2 = - (1/u2)¶Е2/¶t2
2/¶t2 = - (1/u2)¶Е2/¶t2 rot
rot 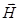 = ¶
= ¶ /¶t = eоe ¶
/¶t = eоe ¶ /¶t;
/¶t;
Из векторного анализа известно, что rot rot  = grad div
= grad div – D
– D , но grad div
, но grad div º 0 и тогда
º 0 и тогда
D = 1/u2)¶
= 1/u2)¶ 2/¶t2, где D = ¶2/¶х2 + ¶2/¶у2 + ¶2/¶z2 - оператор Лапласа - сумма вторых частных производных по пространственным координатам.
2/¶t2, где D = ¶2/¶х2 + ¶2/¶у2 + ¶2/¶z2 - оператор Лапласа - сумма вторых частных производных по пространственным координатам.
В одномерном случае получаем дифференциальное уравнение в частных производных, называемое волновым:
¶ 2/¶х2 - 1/u2)¶
2/¶х2 - 1/u2)¶ 2/¶t2 = 0
2/¶t2 = 0
Такого же типа уравнение получается и для индукции  магнитного поля. Его решением является бегущая плоская монохроматическая волна, задавемая уравнением:
магнитного поля. Его решением является бегущая плоская монохроматическая волна, задавемая уравнением:
 =
=  cos (wt – kх + j) и
cos (wt – kх + j) и  =
= cos (wt – kх + j), где w/k = u = 1/Ö(mоmeоe) - фазовая скорость волны.
cos (wt – kх + j), где w/k = u = 1/Ö(mоmeоe) - фазовая скорость волны.
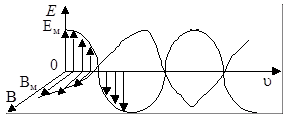 Векторы
Векторы  и
и 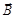 изменяются синфазно во времени, но во взаимно перпендикулярных плоскостях и перпендикулярно направлению распространения (скорости
изменяются синфазно во времени, но во взаимно перпендикулярных плоскостях и перпендикулярно направлению распространения (скорости 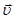 волны):
волны):  ^
^ 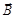 ,
,  ^
^ 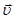 ,
, 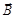 ^
^ 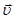 .
.
Свойство взаимоперпендикулярности векторов  и
и 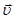 и
и 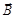 и
и 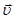 позволяет отнести электромагнитную волну к поперечным волнам.
позволяет отнести электромагнитную волну к поперечным волнам.
В вакууме электромагнитная волна распространяется со скоростью света u = с = 1/Ö(eоmо) = 3×108 м/с, а в вещественной среде волна замедляется, ее скорость убывает в Ö(em) раз, то есть u = с/Ö(em) = 1/Ö(eоmоem).
В каждой точке пространства значения векторов  и
и 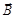 пропорциональны друг другу. Отношение напряжённостей электрического и магнитного полей определяется электрическими и магнитными свойствами (проницаемостями e и m) среды. Это выражение связано с равенством объемных плотностей энергий wэ и wм электрического и магнитного полей волны:
пропорциональны друг другу. Отношение напряжённостей электрического и магнитного полей определяется электрическими и магнитными свойствами (проницаемостями e и m) среды. Это выражение связано с равенством объемных плотностей энергий wэ и wм электрического и магнитного полей волны:
wэ = eоeЕ2/2 = wм = mоmН2/2 Þ Е/Н = Ö(mоm/eоe).
Отношение Е/Н, как нетрудно видеть, имеет размерность сопротивления: В/м: А/м = В/А = Ом. Применительно к вакууму, например, Е/Н = Ö(mо/eо) = 377 Ом - называется волновым сопротивлением вакуума. Отношение же Е/В = 1¤Ö(eоmо) = с = 3×108 м/с (в вакууме).
Распространяющиеся в пространстве электромагнитные колебания (электромагнитные волны) переносят энергию без переноса вещества - энергию электрического и магнитного полей. Ранее мы получали выражения для объёмных плотностей энергии электрического и магнитного полей:
wэ = eоeЕ2/2 и wм = mоmН2¤2 [Дж /м3].
Основной характеристикой переноса энергии волной является вектор 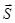 плотности потока энергии, называемый (применительно к электромагнитным волнам) вектором Пойнтинга, численно равный энергии, переносимой через единицу площади поверхности нормальной к направлению распространения волны, за единицу времени: [
плотности потока энергии, называемый (применительно к электромагнитным волнам) вектором Пойнтинга, численно равный энергии, переносимой через единицу площади поверхности нормальной к направлению распространения волны, за единицу времени: [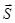 ] = Дж/м2с = Вт/м2.
] = Дж/м2с = Вт/м2.
За единицу времени через единичную площадку пройдёт вся та энергия, которая содержится в объеме V параллелепипеда (цилиндра) с основанием в 1 м2 и высотой равной скорости u распространения волны, то есть пути, проходимому волной за единицу времени:
S = wV = wu = (wэ + wм)¤Ö(eоmоem) = eоeЕ2¤2Ö(eоmоem) + mоmН2¤2Ö(eоmоem) = [Ö(eоe ¤mоm)]Е2/2 + [Ö(mоm ¤eоe)] Н2/2.
Так как Е/Н = Ö(mоm/eоe), то S = ЕН/2 + НЕ/2 = ЕН.
В векторной форме вектор Пойнтинга выразится как произведение векторов напряженностей электрического и магнитного полей: 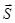 = [
= [
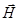 ] = w
] = w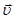 .
.
Простейшим излучателем электромагнитных волн служит электрический диполь, момент  которого изменяется с течением времени. Если изменения электрического момента носят повторяющийся, периодический характер, то такой "колеблющийся диполь" называется осциллятором или элементарным вибратором. Он представляет собой простейшую (элементарную) модель излучательной системы в электродинамике. Любой электронейтральный излучатель с размерами L << l в так называемой волновой или дальней зоне (при r >> l) имеет такое же поле (характер распределения в пространстве) излучения, как и осциллятор с равным дипольным моментом.
которого изменяется с течением времени. Если изменения электрического момента носят повторяющийся, периодический характер, то такой "колеблющийся диполь" называется осциллятором или элементарным вибратором. Он представляет собой простейшую (элементарную) модель излучательной системы в электродинамике. Любой электронейтральный излучатель с размерами L << l в так называемой волновой или дальней зоне (при r >> l) имеет такое же поле (характер распределения в пространстве) излучения, как и осциллятор с равным дипольным моментом.
 Осциллятор называют линейным или гармони- ческим, если у него дипольный момент изменяется по гармоническому закону: Р = Рм sin wt; Рм = q l.
Осциллятор называют линейным или гармони- ческим, если у него дипольный момент изменяется по гармоническому закону: Р = Рм sin wt; Рм = q l.
Как показывает теория излучения, мгновенная мощность N излучения электромагнитных волн гармоническим осциллятором пропорциональна квадрату второй производной изменения его дипольного момента, то есть:
N ~ ïd2Р/dt2ï2; N = mоïd2Р/dt2ï2/6pс = mоw4Рм2sin2 wt/6pс.
Средняя мощноcть < N > излучения диполя за период колебаний равна:
< N > = (1/Т) N dt = mоw4Рм2/12pс
N dt = mоw4Рм2/12pс
Обращает на себя внимание четвертая степень частоты в формуле для мощности излучения. Во многом поэтому для передачи радио- и телеинформации используются высокочастотные несущие сигналы.
Диполь излучает неодинаково в различных направлениях. В волновой (дальней) зоне интенсивность J излучения диполя: J ~ sin2 q ¤r2, где q - угол между осью диполя и направлением излучения. Зависимость J (q) при фиксированном r называется полярной диаграммой направленности излучения диполя. Она имеет вид восьмёрки. Из неё видно, что диполь сильнее всего излучает в направлении q = p/2, то есть в плоскости перпендикулярной оси диполя. Вдоль собственной оси, то есть при q = 0 или q = p, диполь совершенно не излучает электромагнитные волны.
Уравнение бегущей монохроматической волны Е = Ем cos (wt – kх + j) является идеализацией реального волнового процесса. В действительности ему должна соответствовать бесконечная во времени и пространстве последовательность горбов и впадин, перемещающаяся в положительном направлении оси х со скоростью u = w/k. Эта скорость называется фазовой, ибо представляет собой быстроту перемещения в пространстве эквифазовой поверхности (поверхности постоянной фазы). Действительно, уравнение эквифазовой поверхности имеет вид: Ф = (wt – kх + j) = const или, иначе, dФ = 0, то есть wdt - kdх = 0, откуда dх/dt = u = w/k.
Реальные волновые процессы ограничены во времени, то есть имеют начало и конец, и у них меняется амплитуда. Их аналитическое выражение может быть представлено в виде набора, группы, пакета волн (монохроматических):
Е =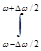 Ем w cos (wt – kw х + jw)dw
Ем w cos (wt – kw х + jw)dw
с близкими частотами, лежащими в узком интервале от w - Dw/2 до w + Dw/2, где Dw << w и близкими (не сильно различающимися) спектральными плотностями амплитуды Ем w, волновыми числами kw и начальными фазами jw.
При распространении в вакууме волны любой частоты имеют одинаковую фазовую скорость u = с = 1¤Ö(eоmо) = 3×108 м/с, равную скорости света. В вещественной среде за счёт взаимодействия электромагнитной волны с заряженными частицами (электронами прежде всего) скорость распространения волн начинает зависеть от свойств среды, её диэлектрической, и магнитной проницаемостей, согласно формуле: u = 1/Ö(eоmоem).
Диэлектрическая и магнитная проницаемости вещества оказываются зависящими от частоты (длины) электромагнитной волны, а, следовательно, и фазовая скорость распространения волны в веществе оказывается разной для разных её частот (длин волн). Этот эффект называется дисперсией электромагнитных волн, а среды называют диспергирующими. Вещественная среда может быть не диспергирующей лишь в некотором, не очень широком диапазоне частот. Совершенно не диспергирующей средой является лишь вакуум.
При распространении в диспергирующей среде волнового пакета, составляющие его волны с различающимися частотами будут обладать различными скоростями и с течением времени будут "разъезжаться" друг относительно друга. Волновой пакет будет в такой среде постепенно расплываться, рассеиваться, что и отражается термином "дисперсия".
Для характеристики скорости распространения волнового пакета как целого принимают скорость распространения его максимума - центра пакета волн с наибольшей амплитудой. Эту скорость называют групповой и, в отличие от фазовой скорости u = w/k, она определяется не через отношение w/k, а через производную u = dw/dk.
Естественно, что в вакууме, то есть в отсутствие дисперсии, фазовая скорость (быстрота перемещения эквифазовой поверхности) и групповая (быстрота переноса энергии волной) совпадают и равны скорости света. Понятие групповой скорости, определяемое через производную (быстроту изменения угловой частоты с ростом волнового числа) применимо только для несильно диспергирующих сред, где не очень сильное поглощение электромагнитных волн. Получим формулу взаимосвязи групповой и фазовой скоростей:
u = dw/dk = u - (kl/k)×du/dl = u - l×du/dl.
В зависимости от знака производной du/dl, групповая скорость u = u - l×du/dl может быть как меньше, так и больше фазовой скорости u электромагнитной волны в среде.
В отсутствие дисперсии du/dl = 0, и групповая скорость равна фазовой. При положительной производной du/dl > 0, групповая скорость меньше фазовой, имеем случай, называемый нормальной дисперсией. При du/dl < 0, групповая скорость волн больше фазовой: u > u, этот случай дисперсии называют аномальной дисперсией.
Причины и механизм явления дисперсии просто и наглядно можно проиллюстрировать на примере прохождения электромагнитной волны через диэлектрическую среду. В ней переменное электрическое поле взаимодействует со связанными в атомах вещества внешними электронами. Напряжённость электрического поля электромагнитной волны играет для электрона роль периодической вынуждающей силы, навязывающей ему вынужденное колебательное движение. Как мы уже анализировали, амплитуда вынужденных колебаний зависит от частоты вынуждающей силы, и в этом и кроются причины дисперсии электромагнитных волн в веществе и зависимости диэлектрической проницаемости вещества от частоты электромагнитной волны.
При смещении электрона, связанного с атомом, на расстояние х от положения равновесия, атом прибретает дипольный момент р = qех, а образец в целом - есть макродиполь с поляризованностью Р = nр = nqеx, где n - число атомов в единице объёма, qе – заряд электрона.
Из связи векторов 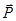 и
и  можно выразить диэлектрическую восприимчивость a, проницаемость e, а затем скорость u электромагнитной волны в веществе:
можно выразить диэлектрическую восприимчивость a, проницаемость e, а затем скорость u электромагнитной волны в веществе:
Р = eоaЕ = nqех Þ a = nqех/eоЕ; e = 1 + a = 1 + nqех/eоЕ; u = с/Ö(em)» с/Öe (при m» 1). Для небольших х: u = с/Ö(1 + nqех/eоЕ)» с/(1 + nqех/2eоЕ).
Отталкиваясь от второго закона Ньютона для упруго связанного с атомом электрона, находящегося в возмущающем электрическом поле Е = Емcos wt электромагнитной волны, найдём его смещение х от положения равновесия в атоме. Полагаем, что смещение х электрона изменяется по закону вынуждающей силы, то есть х = Хмсоs wt.
ma = - kх – ru + Fвын; mх¢¢ = - kх – rх¢ + qеЕ, или, при r = 0 Þ х¢¢ + wо2х = qеЕмcos wt/m,
где wо2 = k/m – собственная частота колебаний электрона, упруго связанного с атомом.
Подставляем решение х = Хмсоs wt в полученное дифференциальное уравнение вынужденных колебаний электрона:
- w2х + wо2х = qеЕм cos wt/m Þ х = qеЕм cos wt/[m(wо2 - w2)] = qеЕ/[m(wо2 - w2)]
Подставляем полученное выражение для смещения х в формулу для фазовой скорости электромагнитной волны:
u» с/(1 + nqех/2eоЕ) = с/[1 + nqе2/2meо(wо2 - w2)]
На частоте w = wо фазовая скорость u электромагнитной волны обращается в ноль.
На некоторой частоте wр, при которой nqе2/meо(wо2 - wр2) = - 1, фазовая скорость волны претерпевает разрыв. Значение этой «резонансной» частоты wр = wо + nqе2/meо» 1017 с-1.
Изобразим полученную зависимость фазовой скорости от частоты и от длины волны. Разрывный характер зависимости u(w), называемой дисперсионной, связан с тем, что мы пренебрегли сопротивлением среды и диссипацией энергии колебаний, положив коэффициент сопротивления r = 0. Учет трения приводит к сглаживанию дисперсионной кривой и устранению разрывов.

 Так как частота w и длина волны l обратно пропорциональны (w = 2pn = 2pс/l), то график дисперсионной зависимости u(l) обратен графику u(w).
Так как частота w и длина волны l обратно пропорциональны (w = 2pn = 2pс/l), то график дисперсионной зависимости u(l) обратен графику u(w).
На участке нормальной дисперсии 1 - 2 фазовая скорость u больше скорости света в вакууме. Это не противоречит теории относительности, ибо реальный сигнал (информация, энергия) передаются с групповой скоростью u, которая здесь меньше скорости света.
Групповая скорость u = u - l×du/dl превышает скорость света с в вакууме на участке аномальной дисперсии 2 – 3, где фазовая скорость u убывает с ростом длины волны l и производная du/dl < 0. Но в области аномальной дисперсии имеет место сильное поглощение, и понятие групповой скорости становится неприменимым.
Лекция 16. Представления о пространстве и времени в современной физике. Объединение пространства со временем в СТО. Относительность классических понятий одновременности, длины и длительности.
В 1905 г А. Эйнштейн впервые оформил в теоретическую систему кинематические, т. е. пространственно-временные представления, «подсказанные» опытом анализа движений с большими, так называемыми релятивистскими (соизмеримыми со скоростью света с = 3×108 м/с в вакууме) скоростями.
В механике Ньютона пространственно-временные представления специально не выделялись и фактически считались очевидными, согласующимися с наглядным опытом медленных движений. Однако предпринятые в XIX в попытки объяснить исходя из этих представлений особенности распространения такого релятивистского объекта как свет, приводили к противоречию с опытом (опыт Майкельсона, 1881 г, 1887 г. и др.). Анализируя возникшую проблемную ситуацию, А. Эйнштейн сумел в 1905 г сформулировать два основополагающих утверждения, называемых постулатами (принципами), согласующихся с опытом релятивистских (высокоскоростных) движений. Эти утверждения, получившие название постулатов Эйнштейна, составили основу его специальной (частной) теории относительности.
1. Принцип относительности Эйнштейна: все законы физики инвариантны по отношению к выбору инерциальной системы отсчета (ИСО), т. е. в любых ИСО законы физики имеют одинаковый вид, не зависят от произвола субъекта (ученого) в выборе ИСО. Или, иначе - все ИСО равноправны, отсутствует какая-либо привилегированная, избранная, абсолютная[5] ИСО. Или, еще - никакими физическими опытами, проводимыми внутри ИСО, нельзя определить, движется она с постоянной скоростью или покоится. Этот принцип согласуется с принципом объективности познания.
До Эйнштейна в механике был известен принцип относительности Галилея, который был ограничен рамками только механических явлений и законов. Эйнштейн фактически обобщил его на любые физические явления и законы.
2. Принцип инвариантности (постоянства) и предельности скорости света. Скорость света в вакууме конечна, одинакова во всех ИСО, т. е. не зависит от относительного движения источника и приемника света и является предельной скоростью передачи взаимодействий. Этот принцип закреплял в физике концепцию близкодействия, сменившую господствовавшую ранее концепцию дальнодействия, основывающуюся на гипотезе о мгновенности передачи взаимодействий.
 Из двух принципов (постулатов) Эйнштейна вытекают важнейшие для кинематики, более общие, чем классические (галилеевские) преобразования, то есть формулы взаимосвязи пространственных и временной координат x, y, z, t одного и того же события[6], наблюдаемого из разных ИСО.
Из двух принципов (постулатов) Эйнштейна вытекают важнейшие для кинематики, более общие, чем классические (галилеевские) преобразования, то есть формулы взаимосвязи пространственных и временной координат x, y, z, t одного и того же события[6], наблюдаемого из разных ИСО.
Возьмем частный случай выбора двух ИСО, при котором одна из них, обозначаемая (К), движется относительно другой, обозначаемой (К¢), со скоростью V вдоль оси х. В начальный момент времени начала координат О и О¢ обеих ИСО совпадали, и оси Y и Y¢, а также Z и Z¢, тоже совпадали. Для этого случая формулы преобразования пространственно-временных координат одного и того же события при переходе от одной ИСО к другой, называемые преобразованиями Лоренца, имеют следующий вид:
х¢ = (х - Vt)/Ö(1 - V2/с2); у¢ = у; z¢ = z; t¢ = (t - Vх/с2)/Ö(1 - V2/с2) -
- прямые преобразования Лоренца (из ИСО (К) в ИСО (К¢);
х = (х¢ + Vt¢)/Ö(1 - V2/с2); у = у¢; z = z¢; t = (t¢ + Vх¢)/Ö(1 - V2/с2) -
- обратные преобразования Лоренца (из ИСО (К¢) в ИСО (К).
Преобразования Лоренца являются более общими, по сравнению с преобразованиями Галилея, которые они содержат в себе как частный, предельный случай, справедливый при малых, дорелятивистских скоростях (u << с и V << с) движений тел и ИСО. При таких, «классических» скоростях, Ö(1 – V2/с2)» 1, и преобразования Лоренца переходят в преобразования Галилея:
х¢ = х - Vt; у¢ = у; z¢ = z; t¢ = t и х = х¢ + Vt¢; у = у¢; z = z¢; t = t¢
В таком соотношении формул преобразования Лоренца и Галилея находит свое проявление важный методологический принцип научно-теоретического познания - принцип соответствия. Согласно принципу соответствия, научные теории диалектически развиваются по пути ступенчатого обобщения - расширения своей предметной области. При этом более общая теория не отменяет прежнюю, частную, а лишь вскрывает ее ограниченность, очерчивает границы и пределы ее справедливости и применимости, и сама сводится к ней в области этих границ.
Термин "специальная" в названии теории относительности Эйнштейна означает как раз, что она сама является ограниченной (частной) по отношению к другой, тоже созданной А. Эйнштейном теории, получавшей название "общая теория относительности". Она обобщает специальную теорию относительности на любые, не только инерциальные системы отсчета.
Из преобразований Лоренца вытекает ряд кинематических следствий, противоречащих наглядным классическим представлениям и давшим основание назвать релятивистскую кинематику и релятивистскую механику в целом теорией относительности.
Что же относительно, то есть, зависимо от выбора ИСО в СТО? Прежде всего, относительным оказывается факт одновременности двух событий, а также длина тела и длительность процесса. В релятивистской динамике в разряд относительных переходит сила, а у некоторых ученых и масса. Следует, однако, помнить, что главным в любой теории является не относительное, а инвариантное (устойчивое, сохраняющееся, неизменное). Релятивистская механика, вскрывая относительность одних понятий и величин, заменяет их другими инвариантными величинами, такими, например, как комбинация (тензор) энергии-импульса.
1. Относительность одновременности событий.
Пусть в ИСО (К) происходят два события, задаваемые координатами x1, y1, z1, t1 и x2, y2, z2, t2, причем t1 = t2, т. е. в ИСО (К) эти события происходят одновременно.
Громадной заслугой Эйнштейна явилось привлечение внимания к тому, что в классической механике Галилея - Ньютона совершенно не было определено, как фиксировать факт одновременности двух событий, находящихся в разных местах. Интуитивно, в соответствии с принципом дальнодействия, предполагающим бесконечной скорость распространения взаимодействий (что достаточно оправдано для медленных движений), считалось очевидным, что разнесенность событий в пространстве не может влиять на характер их временного соотношения.  Эйнштейн же предложил строгий способ установления факта одновременности разноместных событий, основанный на размещении в этих местах синхронизированных часов. Синхронизировать часы он предложил с помощью реального сигнала, обладающего наивысшей скоростью - светового сигнала. Одним из способов синхронизации часов в конкретной ИСО является такой: часы, находящиеся в точке с координатой х будут синхронизированы с единым центром в точке 0 - начале ИСО, если в момент прихода к ним светового сигнала, испущенного из точки 0 в момент tо, они покажут время tх = tо + х/c.
Эйнштейн же предложил строгий способ установления факта одновременности разноместных событий, основанный на размещении в этих местах синхронизированных часов. Синхронизировать часы он предложил с помощью реального сигнала, обладающего наивысшей скоростью - светового сигнала. Одним из способов синхронизации часов в конкретной ИСО является такой: часы, находящиеся в точке с координатой х будут синхронизированы с единым центром в точке 0 - начале ИСО, если в момент прихода к ним светового сигнала, испущенного из точки 0 в момент tо, они покажут время tх = tо + х/c.
Так как синхронизация осуществляется сигналом, обладающим предельно высокой, но не бесконечной скоростью, то часы, синхронизированные в одной ИСО, окажутся разсинхронизированными в другой (и во всех других) ИСО в силу их относительного движения. Следствием этого и является относительность одновременности разноместных событий и относительность временных и пространственных интервалов (длительностей и длин).
Формально этот вывод следующим образом вытекает из преобразований Лоренца:
в ИСО (К¢) событию 1 соответствует момент времени t1¢ = (t1 - Vх1/с2)/Ö(1 - V2/с2), а событию 2 ® момент t2¢ = (t2 – Vх2/с2)/Ö(1 – V2/с2), так, что при t1 = t2, t2¢ – t1¢ = [(х1 – х2)V/с2]/Ö(1 – V2/с2), и два события 1 и 2, одновременные в одной ИСО – в ИСО (К), оказываются неодновременными в другой (в ИСО (К¢).
В классическом (дорелятивистском) пределе, при V << с, t2¢ – t1¢ » 0, факт одновременности двух событий становится абсолютным, что, как уже говорилось, соответствует бесконечной скорости передачи взаимодействий и синхронизирующего сигнала: с ® ¥ или с >> V.
В релятивистской теории одновременность событий оказывается абсолютной лишь
в частном случае одноместных событий: при х1 = х2 всегда при t1 = t2 и t1¢ = t2¢.
2. Относительность длины тел (пространственных интервалов).
Пусть в ИСО (К) вдоль оси х покоится стержень длиной l о = х2 – х1.
ИСО, в которой тело покоится, называется собственной для данного тела, а его характеристики, в данном случае длина стержня, также называются собственными.
В ИСО (К¢), относительно которой стержень движется, и которая называется лабораторной ИСО, длина стержня l ¢ = х2¢ - х1¢ определяется как разность координат концов стержня, зафиксированных одновременно по часам данной ИСО, т. е., при t1¢ = t2¢.
Используя формулы преобразований Лоренца для х1 и х2, содержащие время в штрихованной ИСО (К¢), установим взаимосвязь l и l ¢:
х1 = (х1¢ + Vt1¢)/Ö(1 - V2/с2); х2 = (х2¢ + Vt2¢)/Ö(1 - V2/с2); Þ х2 - х1 = (х2¢ - х1¢)/Ö(1 - V2/с2)
или окончательно: l ¢ = l оÖ(1 - V2/с2) – эта формула выражает закон преобразования длин
(пространственных интервалов), согласно которому в направлении перемещения размеры тел сокращаются. Этот эффект относительности длины тел, их релятивистского сокращения в направлении перемещения, является реальным, а не кажущимся физическим эффектом, но не динамическим, не связанным с каким-либо силовым воздействием, вызывающем сжатие тел и сокращение их размеров. Этот эффект является чисто кинематическим, связанным с выбранным способом определения (измерения) длины и конечностью скорости распространения взаимодействий. Его можно пояснить и так, что понятие длины перестало в СТО быть характеристикой только одного тела, самого по себе, а стало совместной характеристикой тела и системы отсчета (подобно скорости тела, его импульсу, кинетической энергии и т. п.).
Такие характеристики, изменяются для разных тел в одной и той же ИСО, что естественно и привычно для нас. Но так же, хотя и менее привычно, они изменяются и для одного и того же тела, но в разных ИСО. При малых скоростях движения этот эффект зависимости длины тела от выбора ИСО практически незаметен, почему в механике Ньютона (механике медленных движений) он и не обращал на себя внимания.
Подобный же анализ преобразований Лоренца на предмет выяснения соотношения между длительностями двух процессов, измеряемыми из разных ИСО, одна из которых является собственной, т. e. движется вместе с носителем процесса и измеряет его длительность (разностьмоментов конца и начала процесса) о одними и теми же часами, приводит к следующим результатам:
= о(1 - V2с2), где о - собственная длительность процесса (отсчитываемая одними и теми же часами, движущимися вместе с происходящими событиями, а - длительность того же процесса, отсчитываемая разными часами в ИСО, относительно которой носитель процесса движется и в моменты начала и конца процесса он находится в разных ее местах.
Иногда этот эффект интерпретируют так: говорят, что движущиеся часы идут медленнее неподвижных, и отсюда выводят ряд парадоксов, в частности парадокс близнецов. Следует отметить, что вследствие равноправия всех ИСО в СТО, все кинематические эффекты (и сокращения длины в направлении движения, и замедления времени - длительности движущимися относительно носителя процесса часами) являются обратимыми. И хороший пример такой обратимости представляет собой опыт с мю-мезонами, нестабильными частицами, образующимися в результате взаимодействия с атмосферой, бомбардирующих ее космических лучей. Физиков вначале удивило существование этих частиц на уровне моря, где они должны были бы распасться за время их жизни, т. е. не успеть долететь от верхних слоев атмосферы (где они образуются) до уровня моря.
Но дело оказалось в том, что физики вначале применили в расчетах собственное время жизни -мезонов о = 210-6 с, а расстояние, проходимое ими брали лабораторное, то есть
l = 20 км. Но либо в таком случае нужно и длину (путь, проходимый -мезонами) брать собственную, которая оказывается "сокращенной", "укороченной" соответственно множителю (l –V2/с2). Либо нужно не только длину, но и время брать лабораторным, а оно возрастает пропорционально 1/(l–V2/с2). Таким образом, релятивистские эффекты преобразования временных и пространственных интервалов позволили физикам увязать концы с концами в реальном эксперименте и явлении природы.
При малых скоростях V с релятивистская формула преобразования длительностей процессов переходит в классическую . Соответственно длительность в этом предельном случае (приближении) теряет релятивистскую относительность и становится абсолютной, т. е. не зависящей от выбора ИСО.
Пересматривается в СТО и закон сложения скоростей. Его релятивистскую (общую) форму можно получить, взяв дифференциалы от выражений для х, х, t и t, в формулах преобразований Лоренца и, поделив dх на dt и dх на dt, то есть, образовав из них скорости
х = dх/dt и х = dх/dt.
dх = (dх + Vdt)/(l –V2/с2); dt = (dt + Vdх/с2)/(l –V2/с2);
dх/dt = (dх + Vdt)/(dt + Vdх/с2) = (dх/dt + V)/[1 + V(dх/dt)/с2] х = (х + V)(1 + Vх/с2)
dх = (dх - Vdt)/(l –V2/с2); dt = (dt - Vdх/с2)/(l –V2/с2);
dх/dt = (dх - Vdt)/(dt - Vdх/с2) = (dх/dt - V)/[1 - V(dх/dt)/с2] х = (х - V)(1 - Vх/с2)
Формулы х = (х + V)(1 + Vх/с2) и х = (х - V)(1 - Vх/с2) и выражают собой
релятивистские законы сложения скоростей или, иначе говоря, преобразования скоростей
при переходе от ИСО (К) к ИСО (К) и наоборот.
В дорелятивистском пределе малых скоростей c эти формулы переходят в хорошо известные выражения классического (галилеевского) закона сложения скоростей: х = х + V и х = х – V.
Интересно проследить, как релятивистская форма закона сложения скоростей согласована с принципом постоянства скорости света во всех ИСО. Если в ИСО (К) имеем скорость х = с и ИСО (К) движется относительно ИСО (К) тоже со скоростью V = с, то и относительно ИСО (К) скорость света будет по прежнему равна с:
х = (х + V)(1 + Vх/с2) = (с + с)(1 + сс/с2) = с. Классический же закон сложения приводил к результату: х = х + V = с + с = 2с, т. е. противоречил опыту, ибо не содержал
в себе ограничений на "потолок" скоростей.
|
|
|
Дата добавления: 2014-01-06; Просмотров: 1303; Нарушение авторских прав?; Мы поможем в написании вашей работы!