Основные виды математических моделей

ДЛЯ ПОЛУЧЕНИЯ МАТЕМАТИЧЕСКИХ МОДЕЛЕЙ

ОБРАБОТКА РЕЗУЛЬТАТОВ ЭКСПЕРИМЕНТА

В основе обработки результатов активного и пассивного эксперимента с количественными факторами лежит регрессионный анализ. Он включает метод отыскания параметров математической модели (метод наименьших квадратов) и статистическую обработку данных.

Зависимость выходной величины (отклика) 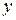от варьируемых факторов , полученная с применением регрессионного анализа, называется регрессионной моделью:

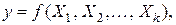(3.1)

где это обозначение некоторой функции от варьируемых факторов, называемой функцией отклика.

Регрессионная модель, таким образом, является частным случаем математической модели объекта. Выходных величин может быть несколько. Например, в процессе обработки детали на станке могут измеряться размеры детали, силы резания и шероховатость поверхности. Тогда зависимость вида (1) строится для каждого отклика. При этом, если по результатам каждого опыта замеряются сразу все отклики, то, по сравнению со случаем единственной выходной величины возрастают только затраты на измерение нескольких откликов и на обработку результатов эксперимента.

Построенная регрессионная модель позволяет получить информацию о самом объекте и о способах управления им. С помощью регрессионной модели легко оценить степень и характер влияния каждого из факторов на выходную величину; модель может послужить основой для оптимизации процесса. Существенно, что вид регрессионной модели должен быть задан заранее, или до проведения эксперимента следует выбрать, к какому классу относится функция 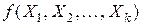. Например, можно искать регрессионную модель в виде многочлена (полинома) определенного порядка, либо в виде экспоненты, тригонометрического многочлена и т. д. Таким образом, при планировании эксперимента для математического описания объекта по результатам опытов рассчитываются только значения констант в регрессионной модели. Если, например, имеется единственный варьируемый фактор 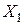, а моделью является экспонента , то для построения модели в явном виде следует по результатам эксперимента вычислить значения коэффициентов 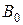и . Возникает вопрос, как выбирается вид регрессионной модели. Здесь исследователю должны помочь знания об объекте, которыми он располагает до постановки эксперимента – априорная информация (от латинского a priori – до опыта). Имеются в виду всевозможные исследования данного объекта, проведенные ранее экспериментаторами и теоретиками, сведения, накопленные технологами и производственниками.

Поскольку вид регрессионной модели постулируется, задается до проведения эксперимента, остается пока открытым вопрос о достоверности такой модели. Чтобы оценить применимость построенной модели, соответствие ее исследуемому объекту, в планировании эксперимента предусмотрена специальная процедура, называемая проверкой адекватности регрессионной модели. По результатам этой проверки исследователь имеет возможность принять или отвергнуть гипотезу о том, соответствует ли построенная модель результатам эксперимента, и, следовательно, пригодна ли она для описания объекта. Наибольшее применение нашли методы планирования эксперимента, в которых регрессионные модели объектов представляются в виде многочленов первого и второго порядка от варьируемых факторов. Модель в виде многочлена первого порядка сокращенно называют регрессионной моделью первого порядка, или линейной. В общем случае, при наличии 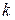варьируемых факторов линейная регрессионная модель объекта имеет вид

(3.2)

где 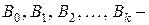коэффициенты, числовые значения которых определяются по результатам эксперимента. Их называют коэффициентами регрессии, а уравнение (2) или, в общем случае, (1) – уравнением регрессии. Коэффициенты , стоящие перед обозначениями факторов , называют линейными коэффициентами регрессии, а коэффициент 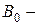свободным членом.

Таким образом, выбор регрессионной модели первого порядка для описания объекта равносилен предположению о линейной зависимости выходной величины от каждого из факторов, т. е. утверждению о том, что выходная величина изменяется пропорционально изменению варьируемого фактора. Кроме того, представление регрессионной модели в виде многочлена первого порядка предполагает отсутствие эффектов взаимодействия между факторами. Это означает, что степень и характер влияния каждого фактора на выходную величину не зависят от уровней варьирования остальных факторов.

Из сказанного следует, что линейная регрессионная модель дает, как правило, приближенное представление о влиянии факторов на объект. Применение таких моделей оправдано в следующих основных случаях: 1) на начальных этапах исследования объекта или в других ситуациях, когда экспериментатора удовлетворяет ограниченная точность линейного приближения; 2) при жестком ограничении на количество опытов, поскольку экспериментальные планы, позволяющие получить линейную модель, являются экономными; в деревообработке это относится, прежде всего, к экспериментам, проводимым в производственных условиях при исследовании процессов сушки, пиления и ряда других; 3) в ситуации, когда экспериментатор уверен в достоверности линейной модели, например, по результатам теоретических исследований.

Обратимся к рассмотрению моделей второго порядка, т. е. моделей в виде многочленов второго порядка от варьируемых факторов. Построим вначале модель второго порядка (иначе – квадратичную модель), например, для трех варьируемых факторов:

(3.3)

Из уравнения (3) ясна общая структура квадратичной модели. Эта модель, рассматриваемая для произвольного числа 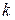факторов, содержит, во-первых, все слагаемые линейной модели: свободный член 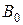, линейные члены . Дополнительно к этому модель второго порядка включает квадратичные члены, являющиеся произведениями коэффициентов регрессии на квадраты факторов: и члены с парными взаимодействиями, которые представляют собой коэффициенты регрессии, умноженные на произведения двух различных факторов, т. е. члены вида:

Зависимость выходной величины от каждого из факторов, полученная на основе квадратичной модели, представляется на графике отрезком параболы, имеющей ветви, направленные либо вверх; либо вниз. Такое представление позволяет достаточно полно описать широкий круг реальных зависимостей. Модель второго порядка удовлетворительно «работает» также при наличии одного максимума или минимума выходной величины в пределах диапазона варьирования факторов.

Описание объекта квадратичной моделью даст заведомо плохие результаты, если: 1) истинная зависимость отклика от некоторого фактора имеет более одного экстремума (рис. 3.1, а); 2) зависимость 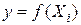имеет точку перегиба (рис. 3.1, б); 3) при некотором значении значение отклика резко (скачком) изменяется (рис. 3.1, в).

В первых двух случаях можно рекомендовать для описания объекта многочлены третьего или более высокого порядка. Другим выходом из положения, пригодным для всех трех случаев, является деление диапазона варьирования факторов на более мелкие поддиапазоны, и изучение объекта для каждой из полученных областей отдельно. Однако правильное выделение областей варьирования требует наличия априорной информации о характере исследуемой зависимости.

а	б	в
Рис. 3.1. Случаи неудовлетворительного описания зависимостей моделями второго порядка

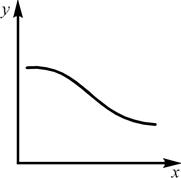
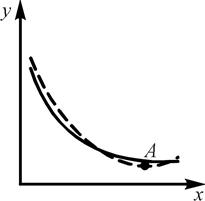
Следует особо отметить случай, если графиком истинной зависимости является кривая, имеющая горизонтальную асимптоту (рис. 3.2). Если такую зависимость описать квадратичной моделью, то соответствующая парабола (штриховая линия) может иметь экстремум внутри диапазона варьирования фактора, который совершенно не соответствует физической картине явления.

Рис. 3.2. Случай зависимости с горизонтальной асимптотой

В данном случае разумно уменьшить диапазон варьирования фактора, исключив его правую часть.

Дата добавления: 2014-01-07