Лекция 5. Операторный метод анализа линейных систем

Раздел 2.

Операторный метод анализа линейных систем.

Иммануил Кант: во всякой науке столько истины, сколько в ней математики,

Давид Гилберт: Математика – основа всего точного естествознания.

Система управления состоит из элементов, имеющих различную физическую природу. Для анализа их взаимодействия удобно перейти к единообразному, стандартному описанию. В инженерной практике наибольшее распространение получил следующий способ:

а) каждый реальный элемент рассматривается как отдельное устройство системы и находится его описание (звено, модель);

б) взаимодействие между звеньями задается путем описания связей между их входами и выходами, т.е. связей, определяющих структуру системы.

1. Описание элементов.

Приступим к изучению свойств отдельных элементов.

Элементом САУ называется устройство, преобразующее один процесс (входное воздействие) в другой процесс (выходную реакцию), другими словами, устройство, которое осуществляет преобразование «вход-выход». Необходимо получить математическую модель элемента, т.е. его описание на каком-либо формальном языке.

Универсальным языком теоретического естествознания, служащим для математического моделирования взаимосвязей процессов в природе и технике, является язык уравнений – алгебраических и, в особенности, дифференциальных.

Под математической моделью элемента мы понимаем ДУ элемента, связывающее выходные и входные величины (сигналы) элемента. ДУ есть описание преобразования «вход-выход» в неявной форме.

Схематическое представление элемента показано на рисунке ниже

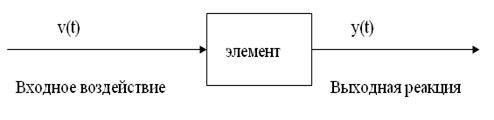
Элемент, представленный своим уравнением (математической моделью), называется звеном.

Обычно уравнение элемента получают аналитическим путем, используя законы природы, которые положены в основу принципа действия элемента (модели типа «белый ящик»). Другой путь - идентификация: определение математической модели сложных элементов, обычно объектов управления, экспериментальным путем (модели типа «черный ящик»).

Первый путь получения математической модели для элементов механической природы использовать законы Ньютона и принцип Даламбера. Последний гласит:

«Состояние равновесия (статическое равновесие) динамической системы, подвергаемой действию внешней движущей силы повинуется следующему принципу, «для любого тела алгебраическая сумма внешних приложенных к нему сил, противодействующих движению в любом направлении, равна нулю».

Для электрических элементов-законы Кирхгофа и Ома. Для электромеханических элементов –законы электротехники и законы механики, для гидравлических элементов-законы гидравлики и т.д.

Наиболее общей математической моделью динамического элемента является нелинейное дифференциальное уравнение (НЛДУ) следующего вида

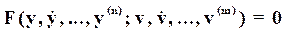, (1)

где

F – нелинейная функция;

; .

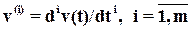Здесь n – порядок уравнения, определяющий и порядок элемента.

Уравнение (1) называют уравнением динамики элемента.

Заметим, что выход динамического (инерционного) элемента зависит от настоящего значения входа и прошлых значений входа и выхода в отличие от статического (безинерционного) элемента, выход которого зависит лишь от настоящего значения входа.

Уравнение статики элемента. Пусть входное воздействие – постоянная величина, 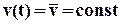, так что

.

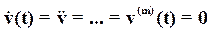Пусть существует такое 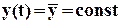, которое обращает уравнение (1) в тождество. При этом

.

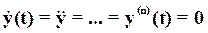Такой режим, с постоянными значениями на входе и выходе, носит название состояние равновесия (покоя, номинальный режим работы, рабочая точка).

Подставляя в уравнение динамики (1) вместо y и v соответственно 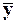и 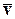, получаем уравнение статики элемента:

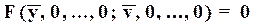. (2)

Разрешая (1) относительно выходного сигнала, находим уравнение статики

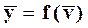, записанное в другом виде. Уравнение статики является нелинейным алгебраическим уравнением (НАУ). График зависимости 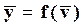называется статической характеристикой элемента. Как пример, на рисунке ниже показана статическая характеристика электронного прибора.

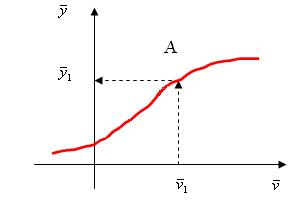
Зная график, легко определить выход 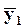по известному входу 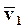, не решая уравнения статики. При этом точка А с координатами (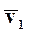,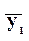) называется рабочей точкой (set point).

Элементы, описываемые нелинейными алгебраическими (НАУ) или нелинейными дифференциальными уравнениями (НЛДУ), называются нелинейными.

Уравнение элемента описывает свойства элемента в неявном виде. Для анализа свойств элемента в явном виде надо решить следующую задачу.

Известно уравнение (1) и v(t), необходимо определить y(t). Если элемент нелинейный, то трудно решить НЛДУ. Но существуют приемы, позволяющие упростить математическую модель. К таким приемам относится в первую очередь линеаризация.

2. Линеаризация – процесс преобразования нелинейной математической модели элемента (1) в эквивалентное, при определенных условиях, линейное ДУ.

Пусть нелинейный элемент находится в состоянии равновесия, при этом выход и вход характеризуются 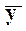и 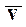. Предположим, что входное воздействие отклонилось от 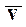, а значит в соответствии с уравнением (1) отклонится и выход y от 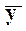, так что

, .

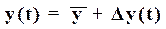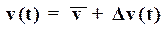Здесь 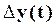- отклонение выхода, 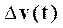- отклонение входа.

Отсюда отклонения от нуля i - ых производных выхода и входа соответственно:

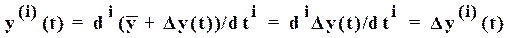
при 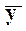=const,

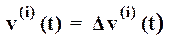
при 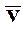=const.

Подставляя в (1) 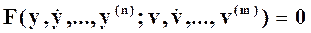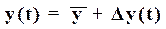,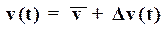получаем уравнение нелинейного элемента в отклонениях (приращениях)

. (3)

Предположим, что нелинейная функция однозначна и дифференцируема по всем своим аргументам, по крайней мере, в окрестности точки А, соответствующей положению равновесия, т.е. существуют частные производные функции F в окрестности точки А. При этом можно разложить F в ряд Тейлора в окрестности точки A с координатами(,):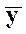

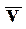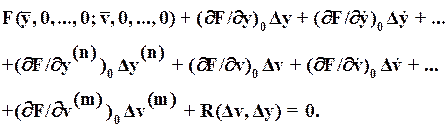(4)

Здесь R – остаточный член разложения в ряд.

Предположим, что отклонения выхода и входа 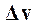и 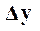, и их производных являются малыми, при этом можем пренебречь R, т.е. считать, что

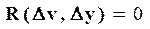
в виду малости по сравнению с другими членами разложения, т.к. он включает слагаемые, содержащие отклонения 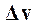и 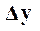в степени выше первой.

Принимая во внимание уравнение (2) 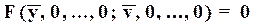и вышесказанное относительно R, можно записать уравнение (4) в виде

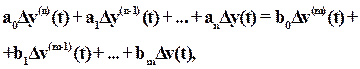(5)

где

, ,

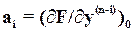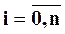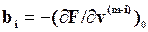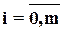, . (6)

Индекс «0» в уравнениях (4) и (6) означает, что после определения частных производных заменяем y на 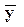, v на 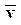. Следовательно, 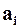и 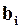- постоянные коэффициенты, а уравнение (5) является линейной математической моделью элемента (ЛДУ с постоянными коэффициентами).

Как видим, сущность линеаризации заключается в замене нелинейного ДУ (3) линейным ДУ (5).

Такая замена справедлива при малых отклонениях входа и выхода элемента, т.е. уравнения (3) и (5) эквивалентны только при выполнении данного условия.

Заметим, что уравнение (5), называемое линеаризованным уравнением элемента, отражает его нелинейные свойства. Действительно, при изменении рабочей точки, т.е. при другом постоянном входе, изменяются в соответствии с выражением (6) коэффициенты уравнения (5).

Пример 1.

Рассмотрим в качестве элемента цепь RL.

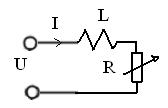
Пусть входной величиной является омическое сопротивление R; а выходной величиной – ток I. Пусть к этой цепи приложено постоянное напряжение U=const.

Уравнение цепи можно представить на основе закона Кирхгофа:

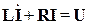
или

.

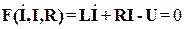Это уравнение – нелинейное ДУ 1-го порядка (уравнение динамики), т.к. входная величина R является коэффициентом при входной величине I, следовательно, n=1, m=0 в уравнении (1)

.

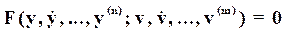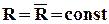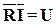Полагая и I=const, и учитывая, что , находим уравнение статики элемента или

.

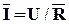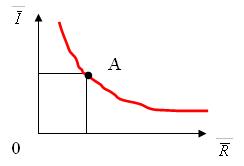
Такому уравнению соответствует статическая характеристика цепи, изображенная на рисунке ниже.

Полагая в уравнении (5)

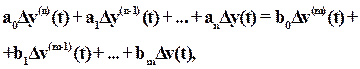
n=1, m=0 и заменяя в нем y на I, v на R, находим линеаризованное уравнение цепи (уравнение линеаризованного звена (ЛДУ))

,

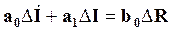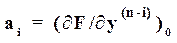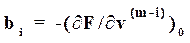,(6)

Коэффициенты определяем с помощью уравнения (6):

,

,

.

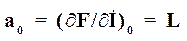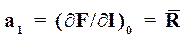При этом линеаризованное уравнение имеет вид

.

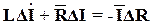Пример 2. Рассмотрим механическую управляемую систему (объект управления масса - пружина-демпфер), показанную на рис ниже, где y, k, m и c(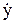) есть положение массы, постояная пружины, масса и сила вязкого трения соответственно.

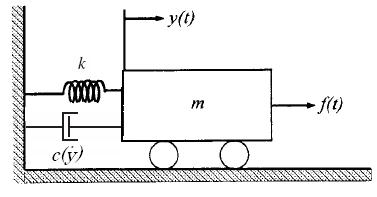
Примем в качестве входной величины приложенную к массе силу f(t), а в качестве выходной величины положение массы y(t). Используя принцип Даламбера, согласно которому сумма моментов, приложенных к телу должна быть равна нулю или эквивалентно второй закон Ньютона (F=ma), получаем уравнение механической системы

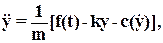
или

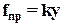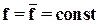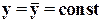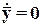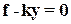где представляет упругую силу пружины. Найденное уравнение является нелинейным дифференциальным уравнением второго порядка в силу нелинейной зависимости силы вязкого трения от скорости перемещения массы, причем n=2, m=0. Полагая и , и учитывая, что , находим уравнение статики элемента или

.

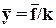В данном случае статическая характеристика элемента линейная и коэффициенты

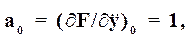
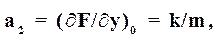
линеаризованного уравнения

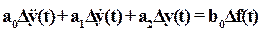
не зависят от выбранного состояния равновесия. Так, если c(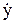)=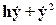, то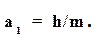

С помощью пакета интерактивных средств обучения ICTools для динамики и управления можно исследовать процесс линеаризации объекта управления в виде бака с жидкостью, описываемого нелинейным дифференциальным уравнением первого порядка 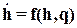. Matlab6.5/Ictools-6.0-windows-new/ictools.m/Linear systems/Modeling of Dynamical Systems/

Математическая модель ОУ:

,

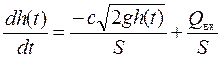(1)

где 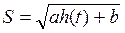– площадь поперечного сечения бака (a и b – константы), с – коэффициент расхода жидкости на оттоке бака, g = 9.8м/с².

Дата добавления: 2014-01-07