Возрастание и убывание функций. Экстремумы функции

Одно из самых важных применений производных состоит в том, что с их помощью можно проводить исследования функций, находить промежутки возрастания и убывания, экстремальные значения функции, а также наибольшее и наименьшее значения непрерывных функций на отрезке.

Необходимое и достаточное условие возрастания и убывания функций

Теорема 6.7. (Необходимые условия). Если дифференцируемая на интервале функция возрастает на данном интервале, то 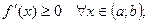если функция убывает на , то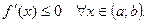

Доказательство. Рассмотрим функцию – возрастающую на интервале 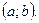Возьмем произвольную точку и 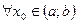зададим приращение так чтобы 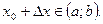Определим отношение 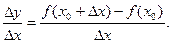Из условия возрастания функции следует, что

при 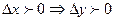, т.е.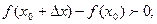

при 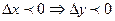, т.е.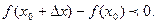

Отсюда ясно, что 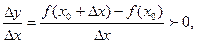так как числитель и знаменатель имеют одинаковые знаки. По условию теоремы функция имеет производную в точке 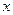и переходя к пределу отношений приращений (строгое неравенство заменяется на нестрогое), получим 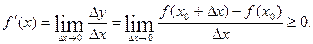Теорема доказана.

Итак, для дифференцируемой функции 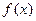необходимое условие монотонности кратко может быть записано следующим образом:

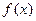– возрастает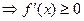 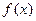– убывает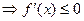

Теорема 6… (Достаточные условия). Если дифференцируемая на интервале 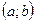функция 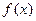имеет 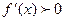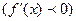для 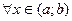, то эта функция возрастает (убывает) на интервале .

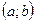Доказательство. Возьмем две произвольные точки такие, что 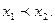По теореме Лагранжа имеем 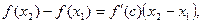где 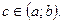По условию 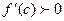и 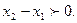Следовательно, 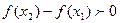или 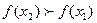, что означает возрастание функции на интервале 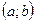. Теорема доказана.

Аналогично доказывается убывание функции.

Итак, для дифференцируемой функции 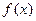достаточное условие монотонности кратко может быть записано следующим образом:

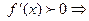
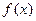– возрастает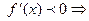 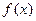– убывает

Геометрически теоремы означают, что в каждой точке графика возрастающей функции касательная образует острый угол с положительным направлением оси Ox (рис.29 a), а в каждой точке графика убывающей функции касательная образует тупой угол с положительным направлением оси Ox (рис. 29 б).

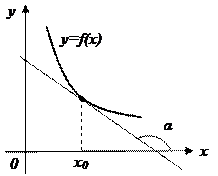
а б

Рис.29

Экстремумы функции

Пусть функция определена на промежутке 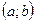и 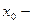внутренняя точка этого промежутка.

Точка называется точкой максимума функции , если в некоторой окрестности этой точки при 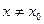верно неравенство 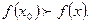Значение 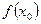называется максимумом функции .

Точка называется точкой минимума функции , если в некоторой окрестности этой точки при 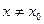верно неравенство 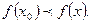Значение 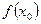называется м инимумом функции .

Максимумы и минимумы функции называют экстремумами функции.

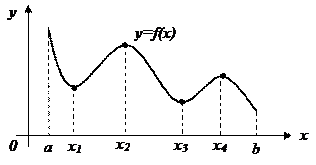Рис.30

Для графика функции 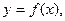изображенном на рис. 30, 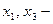точки минимума, 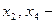точки максимума, значения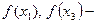минимум функции, 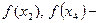максимум функции.

Замечание 1. Функция на данном промежутке может иметь не один экстремум, причем некоторые из минимумов могут быть больше некоторых из ее максимумов.

Замечание 2. Экстремальные точки функции должны быть внутренними для области определения данной функции; конечные значения области определения не могут относиться к экстремальным, так как они не принадлежат области определения вместе с некоторой своей окрестностью слева или справа.

Замечание 3. Экстремальные значения функции нельзя смешивать с понятием наибольшего и наименьшего значения функции на промежутке. Экстремальное значение функции в точке – это максимальное или минимальное по отношению к близлежащим значениям. Под наибольшим (наименьшим) значением функции на отрезке понимают такое значение, больше (меньше) которого нет ни в одной точке, включая концы отрезка.

Теорема .. (необходимое условие экстремума)

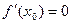Если дифференцируемая функция имеет экстремум в точке , то или 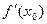не существует.

Доказательство следует из теоремы Ферма.

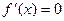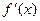Критическими точками (подозрительными на экстремум) непрерывной функции называются внутренние точки области определения, в которых или не существует.

Теорема… (первое достаточное условие экстремума ). Если непрерывная функция дифференцируема в некоторой окрестности критической точки и пи переходе через нее (слева направо) производная 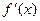меняет знак с плюса на минус, то есть точка максимума; с минуса на плюс, то есть точка минимума.

Доказательство основано на признаке монотонности функции: при смене знака 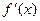с «+» на «–» функция от возрастания переходит к убыванию, значит, 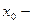точка максимума.

Дата добавления: 2014-01-07