Лекция 13

План лекции

1. Свертка функций. Теорема об изображении свертки функций.

2. Изображение запаздывающей функции.

3. Изображение -функции и ее производных.

4. Дифференцирование в комплексной области.

Теорема 6.

Если функции f₁(t) и f₂(t) являются оригиналами и имеют соответственно изображения F₁(s) и F₂(s), то

L[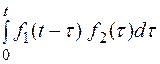] = F₁(s)∙ F₂(s)

Теорема утверждает, что произведению изображений в вещественной области соответствует интеграл свертки.

Доказательство.

Обозначим F(s) = L[]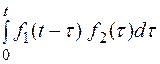

По определению

F(s) =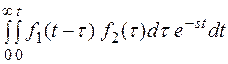

Верхний предел во внутреннем интеграле можно перенести из т. t в т. ∞, если подынтегральное выражение умножить на 1().

Рис. 1.

F(s) =

Изменим порядок интегрирования

F(s) =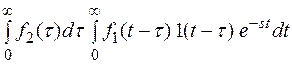

Принимая во внимание вид функции 1(t-τ) как функции аргумента t, запишем

F(s) =

Для второго интеграла введем подстановку 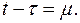Отсюда следует, что

;

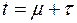
F(s) =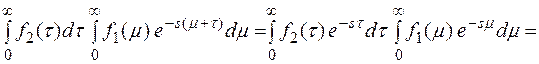

=

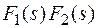
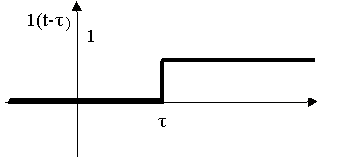
Рис. 2.

Замечание.

Может показаться на первый взгляд, что теорему свертки удобно использовать для вычисления обратного преобразования Лапласа. На самом деле это не так, интеграл свертки приводит к громоздким вычислениям.

7. Изображение запаздывающей функции.

Теорема 7.

Если функция f(t) является оригиналом и имеет изображение F(s), то преобразование Лапласа запаздывающей функции:

при условии

при t < τ. (*)

Доказательство.

По определению

F(s) =

Положим , тогда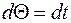

F(s) =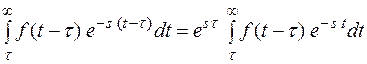

Принимая во внимание соотношение при t < τ нижний предел можно перенести из т. τ в т.0. Получим

F(s) = 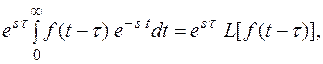отсюда следует, что

.

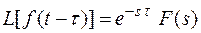Замечание 1.

По условию теоремы функция f(t) является оригиналом, следовательно, может быть записана в виде: f(t)·1(t). Запаздывающий оригинал имеет вид:

, т. е. запаздывающий оригинал обязательно удовлетворяет условию (*).

Замечание 2.

При пользовании данной теоремой во избежание ошибок оригинал следует записывать в видеf(t)·1(t).

Пример 1.

Найти L[]

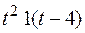По теореме 7 найдем функцию f(t)·1(t)

f(t-4)·1(t-4) = t² 1(t-4). Очевидно

f(t)·1(t) = (t + 4)² 1(t)

по теореме запаздывания

L[] =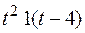

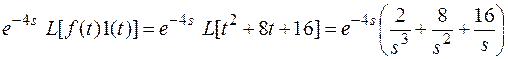
Пример 2.

Найти

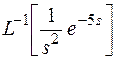
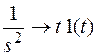
по теореме запаздывания

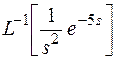= (t – 5) 1(t – 5).

8. Предельный переход по второй независимой переменной.

Теорема 8.

Пусть а – переменная независящая от t и s. Если функция f(t,а) является оригиналом относительно переменной t и имеет изображение F(s,a), то при условии существования выписанных ниже пределов справедливо равенство:

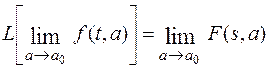
Доказательство.

По определению

Перейдем к пределу

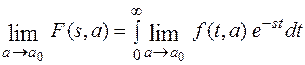
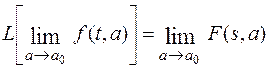
Используя эту теорему, найдем изображение δ - функции. Рассмотрим функцию f(t,a), изображенную на рисунке.

Очевидно,

f(t,a) =

L[f(t,a)] =

L[f(t- τ)] = где

Рассмотрим предел

т.о.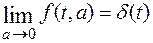

В соответствии с теоремой 8:

L[δ(t)] =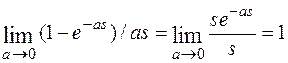

Т. о. Получили L[δ(t)] = 1.

Для производной δ(t) справедливо соотношение

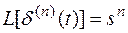
Это равенство формально может быть получено применением теоремы 2.

Для запаздывающей δ(t) справедливо соотношение

L[δ(t-τ)] =

L[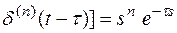(в соответствии с теоремой 7).

9.Дифференцирование в комплексной области.

Теорема 9.

Если функция f(t) является оригиналом и имеет изображение F(s), то

L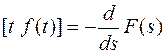

Теорема утверждает, что дифференцирование изображений в вещественной области соответствует умножению оригинала на аргумент t.

Доказательство.

По определению

F(s) =

Продифференцируем равенство по s. Это возможно, т. к. F(s)- аналитическая функция в области Re s > .

F(s) =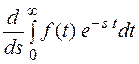

Перейдем к дифференцированию под знаком интеграла, получим

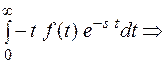
F(s) = L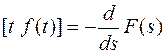

В соответствии с таблицей

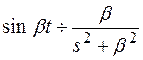
По теореме 9

L[

L[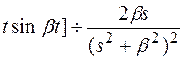

Аналогично

L[

Дата добавления: 2014-01-07