Тобто похідна складеної функції дорівнює добутку похідної заданої функції по проміжному аргументу на похідну цього аргументу по незалежній змінній

Таблиця похідних.

(u = u (x), v=v (x), – диференційовні функції від x)

1. ;

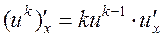2. ;

3. .

4. .

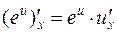5. .

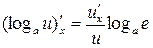6. .

7. .

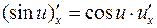8. .

9. .

10. .

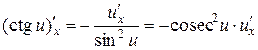11. .

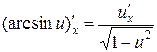12. .

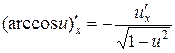13. .

14. .

Приклад. Знайти похідні функцій:

1) ; 2) ; 3) ;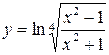

4) y = (1 + sin³ 5 x)²; 5) 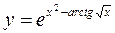; 6) .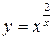

Розв’язання. Використовуючи таблицю похідних, дістанемо:

1)

;

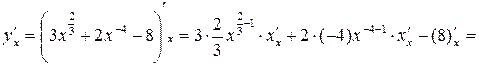
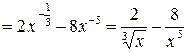2)

;

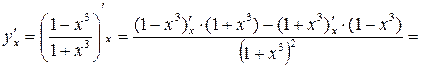
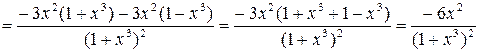3)

;

4)

;

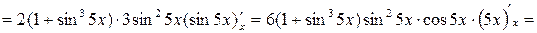
5)

;

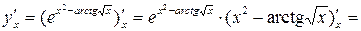
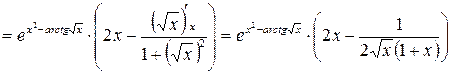6)

.

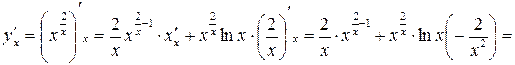
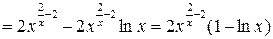Похідна степенево-показникової функції (формула Лейбніца-Бернуллі).

Степенево-показниковою функцією називають функцію, у якої і основа, і показник є змінні, тобто функцію y(x) = u(x)^v(x), (u (x) > 0).

Для виведення формули її похідної прологарифмуємо обидві частини рівності y = u^v. Маємо: ln |y | = v ln u, (u > 0).

Тоді

; ;

; ;

.

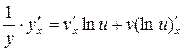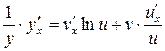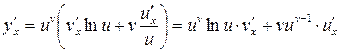Отже, маємо формулу

,

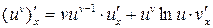за якою похідна степенево-показникової функції дорівнює сумі по­хід­них: степеневої функції (якщо v (x) вважати сталою) та показникової функції (u (x) вважається сталою).

Об’єднуючи встановлені формули та правила диференціюван­ня, дістанемо таблицю похідних, за допомогою якої і знаходять похідні елементарних функцій.

Диференціювання неявних і параметрично заданих функцій. Рівняння дотичної і до кривої

1. Диференціювання неявно заданих функцій

Нехай функція y = y (x) задана неявно рівнянням F (x, y) = 0. Для знаходження похідної 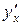цієї функції потрібно про­диференціювати обидві частини заданого рівняння по x, вважаючи y функцією від x, а потім з одержаної рівності виразити .

Приклад. Знайти , якщо y (x) визначається рівнянням:

1) x ² + y ² = R ²; 2) y = cos (x + y).

Розв’язання. 1) Знайдемо похідну по аргументу x від обох час­тин заданого рівняння. Дістанемо

; 2 x + 2 y ·= 0; x + y ·= 0

і виразимо з останньої рівності:

.

2) Аналогічно маємо:

; ;

; ;

; .

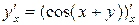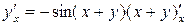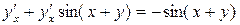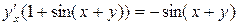З наведених прикладів бачимо, що похідна неявної функції ви­ражається через незалежну змінну і саму функцію. Тому для обчис­лення значення похідної неявної функції при деякому значенні аргу­менту x = x ₀ потрібно знати і значення самої функції в точці x ₀.

2. Диференціювання параметрично заданих функцій

Нехай функція y = y (x) задана параметрично рівняннями

x = x (t), y = y (t) (T ₀ £ t £ T ₁), (1)

де x (t), y (t) – диференційовні функції від t. Потрібно знайти похідну функції y = y (x), тобто .

Якщо функція x = x (t) на відрізку [ T ₀, T ₁] має диференційовну обернену функцію t = j(x), тоді, враховуючи (1), будемо мати

y = y (t), t = j(x),

тобто y є складеною функцією аргументу x. За правилом диференцію­вання складеної функції дістаємо

,

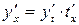де , тобто

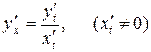. (2)

Виведена формула дозволяє знаходити похідну 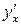функції, за­даної параметрично, не знаходячи безпосередньої залежності y від x.

Приклад. Знайти , якщо

x = R (t – sin t), y = R (1 – cos t).

Розв’язання. Нагадаємо, що це-рівняння циклоїди. Зна­ходимо 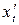та 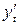: 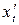= R (1 – cos t), 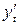= R sin t. Тепер

.

3. Рівняння дотичної і нормалі до кривої

Нехай рівняння y = f (x) є рівняння деякої кривої, яка в точці M ₀(x ₀, f (x ₀)) має дотичну, тобто функція y = f (x), диференційовна при
x = x ₀. Проведемо через точку M ₀(x ₀, f (x ₀)) кривої y = f (x) дотичну M ₀ T.

Означення. Нормаллю (рис.1) до кривої y = f (x) називається пряма, яка проходить через точку дотику M ₀(x ₀, f (x ₀)) перпендикуляр­но до дотичної в цій точці (пряма M ₀ R).

Рівняння дотичної шукаємо у вигляді:

y – y ₀ = k (x – x ₀),

де k = tg a – кутовий коефі­цієнт прямої. Із геометричного змісту похідної відомо, що
tg a = f ¢(x ₀). Отже, рівняння до­тичної до кривої y = f (x), прове­де­ної в точці M ₀(x ₀, f (x ₀)), має вигляд

y – y ₀ = f ¢(x ₀)(x – x ₀), (3)

де y ₀ = f (x ₀).

Як відомо, кутові коефіцієнти взаємно перпендикулярних пря­мих зв’язані рівністю k ₁· k ₂ = – 1. Тому кутовий коефіцієнт нормалі до кривої, проведеної в точці M ₀(x ₀, f (x ₀)), дорівнює і рів­няння нормалі має вигляд:

. (4)

Означення. Кутом a між двома криви­ми, що перетинаються в точці M ₀ (x ₀, y ₀), нази­вається кут між дотичними до цих кривих у точці їх перетину. На рис. 2 це кут TM ₀ T ₁ = q.

Цей кут можна знайти за формулою:

.

Приклад. Скласти рівняння дотичної і нормалі до кривої y = x ³

в точці M ₀(1, 1).

Розв’язання. Рівняння дотичної має вигляд (3):

y – y ₀ = f ¢(x ₀)(x – x ₀),

де x ₀ = 1, y ₀ = 1. Маємо y ¢ = (x ³)¢ = 3 x ².Тоді f ¢(x ₀) = f ¢(1) = 3. Отже, шу­кане рівняння дотичної:

y – 1 = 3(x – 1); 3 x – y – 2 = 0.

Рівняння нормалі має вигляд (4)

,

тобто , або x + 3 y – 4 = 0.

Приклад. Довести, що рівняння дотичної до еліпса 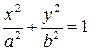у точці дотику M ₀(x ₀, y ₀) має вигляд

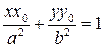. (8)

Розв’язання. Рівнянням функція у (х) задана неявно. Знайдемо як похідну неявно заданої функції. Дістанемо:

; ; .

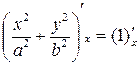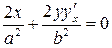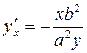Підставимо в координати точки M ₀(x ₀, y ₀) і складемо рівнян­ня дотичної за формулою (3)

.

Виконаємо очевидні перетворення:

.

Поділивши на a ² b ², матимемо

.

Права частина останньої рівності дорівнює 1 тому, що точка M ₀(x ₀, y ₀) лежить на еліпсі (її координати задовольняють рівняння еліпса). Отже, формула (8) доведена.

Аналогічний вигляд мають рівняння дотичних до гіперболи та параболи у точці дотику M ₀(x ₀, y ₀). А саме:

гіпербола – дотична ;

парабола y ² = 2 px – дотична yy₀ = p (x + x ₀).

Приклад. Скласти рівняння дотичної та нормалі до лінії x = 2 e^t, y = e^-t при t ₀ = 0.

Розв’язання. Використаємо формули (6) та (7). Знахо­димо координати точки дотику: x ₀ = 2 e ⁰ = 2, y ₀ = e ⁰ = 1, тобто М ₀ (2, 1) – точка дотику. Далі знаходимо похідні , і обчислюємо їх при t = 0: 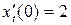, . Тепер, у відповідності з (6), (7), дістанемо шукане рівняння дотичної

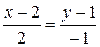, або x + 2 y – 4 = 0,

і рівняння нормалі

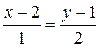, або 2 x – y – 3 =0

Дата добавления: 2014-01-07