Гидравлика 8 страница

Проекции этой силы на оси х, у и z (рис. 6.3) представляют собой горизонтальные и вертикальную составляющие, величины которых соответственно равны

;

;

.

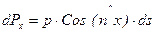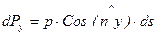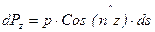так как проекциями орта нормали на оси координат являются косинусы углов между нормалью и соответствующей осью координат.

Из рис. 6.3 видно, что

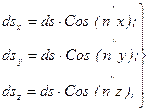; (6.8)

Тогда составляющие силы давления, действующей на площадку ds, можно представить в виде

;

;

.

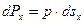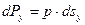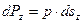Если воспользоваться формулой (6.7) и пренебречь атмосферным давлением, то последние зависимости примут вид

;

;

.

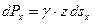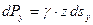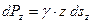Напомним, что индекс у буквы s означает проекцию площадки ds на плоскость, перпендикулярную соответствующей оси.

Компоненты сил давления на всю рассматриваемую криволинейную поверхность, погруженную в жидкость, будут равны

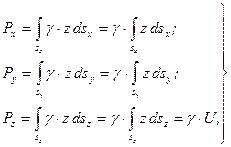(6.9)

где U - объем жидкости, заключенный между рассматриваемой криволинейной поверхностью и поверхностью жидкости.

На рис. 6.3 этот объем ограничен поверхностью AA'BB'CC'. Таким образом, вертикальная составляющая суммарного давления жидкости на криволинейную стенку равняется весу жидкости в объеме цилиндрической поверхности с вертикальными образующими, ограниченной снизу криволинейной стенкой и сверху поверхностью жидкости.

Горизонтальные составляющие суммарной силы давления на криволинейную стенку, как видно из формул, тоже определяются через веса некоторых объемов.

Главный вектор сил давления на стенку по величине равен

.

Точка приложения главного вектора, называемая центром давления, определяется для криволинейной стенки довольно сложно.

Найдем главный вектор и центр давления для плоской стенки s, расположенной под некоторым углом к горизонту (рис. 6.4).

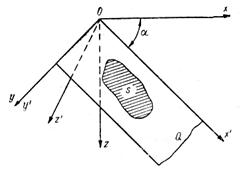
Рис. 6.4. Главный вектор и центр давления

для плоской стенки

Для этого проведем плоскость Q, включающую стенку s, до ее пересечения с поверхностью жидкости и расположим две системы координат, имеющих общее начало в точке О, так, чтобы плоскость хОу одной системы лежала на поверхности жидкости, а плоскость системы x'Oy' совпадала с плоскостью Q. Если оси у и у' совместим с прямой, образованной от пересечения плоскости Q с поверхностью жидкости, то угол между осями х и x' будет равен углу 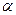наклона плоскости стенки. Ось z' будет нормалью к Q и s. Тогда в соответствии с выражениями (6.8) получим

;

;

.

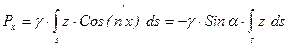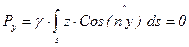Откуда величина главного вектора будет равна

.

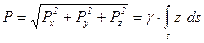Последний интеграл равен площади стенки s, умноженной на координату 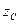центра инерции или центра тяжести этой площадки. Следовательно, окончательно получим

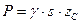. (6.10)

Так как , то .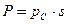

Это означает, что сила давления жидкости на плоскую стенку определяется весом цилиндрического столба этой жидкости с площадью основания, равной площади стенки, и высотой от поверхности до центра тяжести стенки. Если воспользоваться последней формулой, то следует, что главный вектор сил давления на плоскую стенку по величине равен произведению гидростатического давления в центре тяжести стенки на ее площадь.

Точка приложения главного вектора, называемая центром давления, в общем случае не совпадающая с центром тяжести, может быть определена на основании законов статики твердого тела. Известно, что момент главного вектора системы сил равен сумме моментов составляющих сил, т.е. если обозначим координаты центра давления 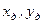и 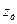, то уравнения моментов относительно осей координат будут

;

;

.

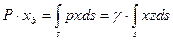Из системы этих трех уравнений можно найти три неизвестные величины: 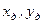и .

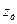Нетрудно показать, что центр давления расположен ниже центра тяжести. Если в последнем соотношении заменим р по формуле (6.10) и разделим обе части на , то получим

.

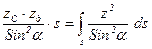Как известно, интеграл, стоящий в правой части, называется моментом инерции площади относительно оси Оу. Если представить соответствующий момент инерции относительно параллельной этой оси прямой, проходящей через центр тяжести, в виде 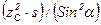и вспомнить, что момент инерции относительно оси, проходящей через центр инерции, меньше момента инерции относительно любой другой параллельной оси, то можно написать неравенство

.

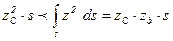Сократив обе части неравенства на , окончательно получим .

6.3. Относительный покой (равновесие) жидкости

Ранее было рассмотрено в основном равновесие жидкости под действием лишь одной массовой силы - ее веса. Этот случай имеет место тогда, когда жидкость покоится в сосуде, неподвижном относительно Земли, а также в сосуде, движущемся равномерно и прямолинейно. Если же сосуд с жидкостью находится в неравномерном или непрямолинейном движении, то на частицы жидкости кроме силы тяжести действуют еще силы инерции, причем если они постоянны по времени, то жидкость принимает новое положение равновесия. Такое равновесие жидкости называется относительным покоем.

При относительном покое свободная поверхность жидкости и прочие поверхности уровня могут существенно отличаться от поверхностей уровня при покое жидкости в неподвижном сосуде, т.е. от горизонтальной плоскости. При определении формы и положения свободной поверхности жидкости, находящейся в относительном покое, следует руководствоваться основным свойством всякой поверхности уровня, которое заключается в следующем: равнодействующая массовых сил всегда действует нормально к поверхности уровня. В самом деле, если бы равнодействующая массовая сила действовала под некоторым углом к поверхности уровня, то касательная составляющая этой силы вызывала бы перемещение частиц жидкости вдоль поверхности уровня. Однако в состоянии относительного покоя отсутствуют какие-либо перемещения частиц жидкости как относительно стенок сосуда, так и друг относительно друга. Следовательно, единственно возможным направлением равнодействующей массовой силы является направление, нормальное к свободной поверхности, а также и к другим поверхностям уровня.

Поверхности уровня не могут между собой пересекаться, иначе по линии пересечения двух таких поверхностей был бы получен ряд точек, давление в которых в одно и тоже время имело бы два разных значения, что невозможно.

Рассмотрим два характерных случая относительного покоя жидкости: в сосуде, движущемся прямолинейно и равноускоренно и в сосуде, вращающемся вокруг вертикальной оси с постоянной угловой скоростью.

Пусть сосуд с жидкостью движется прямолинейно с постоянным ускорением a. В этом случае результирующую массовую силу, действующую на жидкость, найдемкак сумму векторов силы инерции, направленной в сторону, обратную ускорению a и силы тяжести (рис. 6.5).

Обозначив вектор равнодействующей массовой силы, отнесенной к единице массы, через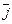, получим

, (6.11)

где и - векторы единичных сил инерции и тяжести.

Для всех частиц рассматриваемого объема жидкости равнодействующие массовые силы параллельны друг другу, а поверхности уровня перпендикулярны к этим силам, поэтому

Рис. 6.5. Силы, действующие при относительном покое

жидкости и прямолинейном равноускоренном

движении сосуда

все поверхности уровня, в том числе свободная поверхность, являются плоскостями, параллельными друг другу. Угол наклона этих плоскостей к горизонту определяется из условия перпендикулярности их к силе .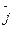

Для определения положения свободной поверхности жидкости в сосуде, движущемся прямолинейно равноускоренно, необходимо к предыдущему условию добавить уравнение объемов, т.е. нужно знать объем жидкости в сосуде и выразить его через размеры сосуда В, Н и первоначальный уровень жидкости h.

Возьмем, например, около точки М площадку dS, параллельную свободной поверхности, и на этой площадке построим цилиндрический объем с образующей, нормальной к свободной поверхности. Условие равновесия указанного объема жидкости в направлении нормали к свободной поверхности будет иметь вид

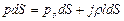, (6.12)

где последний член представляет собой полную массовую силу, действующую на выделенный объем жидкости, а l - расстояние от точки М до свободной поверхности. После сокращения на dS получим

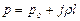. (6.13)

В частном случае, когда а = 0 и соответственно j = g, формула (6.13) превращается в основное уравнение гидростатики.

То же уравнение (6.13) можно получить интегрированием дифференциального уравнения (6.5). Для этого одну из координатных осей удобнее направить вдоль линии действия результирующей массовой силы j. Приняв такое направление, например, для оси z, будем иметь:

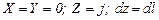. (6.14)

Следовательно, вместо уравнения (6.5) можно записать:

, (6.15)

или после интегрирования и определения постоянной подстановкой параметров свободной поверхности

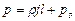. (6.16)

Полученное уравнение совпадает с формулой (6.13).

Возьмем открытый цилиндрический сосуд с жидкостью и сообщим ему вращение с постоянной угловой скоростью w вокруг его вертикальной оси. Жидкость постепенно приобретет ту же угловую скорость, что и сосуд, а свободная поверхность ее видоизменяется; в центральной части уровень жидкости понизится, у стенок - повысится, и вся свободная поверхность жидкости станет некоторой поверхностью вращения (рис. 6.6).

На жидкость в этом случае будут действовать две массовые силы - сила тяжести и центробежная сила, которые, будучи отнесенными к единице массы, соответственно равны g и w²r.

Рис. 6.6. Поверхность жидкости при вращении открытого

сосуда вокруг вертикальной оси

Равнодействующая массовая сила j увеличивается с увеличением радиуса за счет второй составляющей, а угол наклона ее к горизонту уменьшается. Эта сила нормальна к свободной поверхности жидкости, поэтому наклон этой поверхности с увеличением радиуса возрастает. Найдем уравнение кривой АОВ в системе координат z и r с началом в центре дна сосуда. Учитывая, что сила j является нормалью к кривой АОВ, из чертежа находим

tg a = dz/dr = w²r/g, (6.17)

откуда dz = w²rdr/g, или после интегрирования

z = w²r²/(2g) + C. (6.18)

В точке пересечения кривой АОВ с осью вращения r = 0, z = h = С, поэтому окончательно будем иметь:

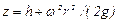, (6.19)

т.е. кривая АОВ является параболой, а свободная поверхность жидкости - параболоидом. Такую же форму имеют и другие поверхности уровня.

Пользуясь уравнением (6.19), можно определить положение свободной поверхности в сосуде, например максимальную высоту Н подъема жидкости и высоту h расположения вершины параболоида при данной угловой скорости w. Для этого необходимо использовать еще уравнение объемов: объем неподвижной жидкости равен ее объему во время вращения.

Для определения закона изменения давления во вращающейся жидкости в виде функции радиуса и высоты выделим вертикальный цилиндрический объем жидкости с основанием в виде элементарной горизонтальной площадки dS (точка М) на произвольном радиусе r и высоте z и запишем условие его равновесия в вертикальном направлении. С учетом уравнения (6.19) будем иметь

.

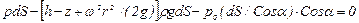После сокращений получим

. (6.20)

Это значит, что давление возрастает пропорционально радиусу и уменьшается пропорционально высоте z. Если сосуд, вращающийся вокруг вертикальной оси, имеет крышку и заполнен жидкостью доверху, то ее форма измениться не может, но изменяется давление в соответствии с выражением (6.20).

Уравнение свободной поверхности жидкости можно найти, если положить р = р₀ После сокращений и преобразований уравнения (6.20) будем иметь

. (6.21)

7. МОДЕЛЬ ИДЕАЛЬНОЙ (НЕВЯЗКОЙ) ЖИДКОСТИ

7.1. Модель идеальной (невязкой) жидкости.

Уравнения Эйлера

Из всех моделей жидкости, рассматриваемых в гидромеханике, наиболее простой является модель идеальной жидкости. Идеальной жидкостью называют жидкость, в которой отсутствуют внутреннее трение и теплопроводность. Таким образом, при движении идеальной жидкости касательных сил трения нет и все взаимодействие между соприкасающимися объемами жидкости сводится к действию нормальных поверхностных сил.

Допущение об отсутствии касательных поверхностных сил означает, что недиагональные компоненты напряжений в точке движущейся жидкости, приведенные в выражении (4.14), обращаются в нуль

.

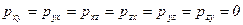Это допущение относится не только к площадкам, нормальным к осям произвольно выбранной системы координат, но и к любой наклонной к координатным осям площадке. Тогда, согласно выражениям (4.13), можно написать проекции напряжения сил давления, нормальных к произвольно направленной площадке

;

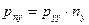и .

есть проекции напряжения 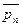на координатные оси, равные

.

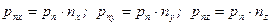Приравнивая правые части соответствующих проекций, получим

. (7.1)

Равенство (7.1) означает, что при движении идеальной жидкости, так же как при состоянии равновесия любой сплошной среды, нормальное напряжение в данной точке не зависит от направления площадки, к которой оно приложено.

В гидростатике и гидродинамике скалярную величину нормального напряжения давления в данной точке потока идеальной жидкости будем называть гидродинамическим давлением или давлением в данной точке. Знак минус означает, что гидродинамическое давление направлено в сторону, противоположную внешней нормали площадки.

Модель идеальной жидкости существенно упростила математическую постановку задач гидромеханики, поэтому долгие годы классическая гидромеханика занималась лишь изучением движения идеальной жидкости.

Несмотря на то что идеальная жидкость в действительности не существует, многие теоретические решения, полученные в предположении идеальности жидкости, имеют большое практическое значение. Пригодность модели идеальной жидкости, для многих задач обтекания тел объясняется прежде всего тем, что идеальная жидкость сохраняет основные свойства реальных жидкостей (непрерывность или сплошность). Кроме того, при обтекании хорошо обтекаемых тел (крыла самолета, ракеты, лопатки турбины и пр.) влияние вязкости на распределение давления по поверхности этих тел сказывается лишь в очень слабой степени. Однако влияние вязкости оказывает решающее значение при подсчете сопротивлений тел в движущейся жидкости.

Для вывода уравнения движения воспользуемся уравнением в напряжениях (5.11), проекция которого на ось х будет

где - проекция ускорения;

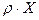- проекция массовой силы, отнесенной к единице объема.

Остальные три слагаемых представляют собой производные от нормальных и касательных напряжений в жидкости.

Так как в идеальной жидкости вязкость отсутствует, а касательные напряжения равны нулю, то величина нормальных напряжений будет 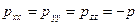. Поэтому уравнения движения идеальной жидкости в проекциях на оси координат имеют вид

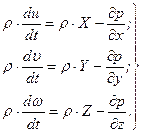(7.2)

Полученную систему уравнений в векторной форме можно представить в виде

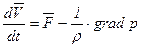. (7.3)

Это уравнение движения идеальной жидкости часто называют уравнением Эйлера.

Для жидкости, находящейся в покое, из уравнения (7.3) можно получить известное уравнение гидростатики, приравняв к нулю производные от скорости по времени. В этом случае жидкость находится в равновесии под действием только массовых и поверхностных сил и уравнения примут вид

;

;

.

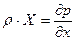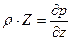В общем случае скорость движения жидкости зависит как от координат, так и от времени, поэтому

.

Подставив соответственно выражение для и в уравнение (7.2), получим следующий вид дифференциальных уравнений движения (уравнений Эйлера)

(7.4)

Для интегрирования дифференциальных уравнений движения необходимо иметь некоторые начальные и граничные условия. Пусть обтекаемое тело будет неподвижным. Так как поверхность этого тела является поверхностью тока и через нее жидкость не течет, то нормальная составляющая скорости в точках поверхности тела равна нулю, т.е. .

Идеальная жидкость лишена вязкости, поэтому при обтекании тела частицы ее скользят по поверхности и касательная составляющая скорости в точках поверхности тела не равна нулю, т.е. .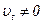

Начальные условия могут быть заданы в виде значений проекций скорости на некоторой поверхности в потоке в момент времени .

В какой-либо точке потока должна быть известна также величина давления, а в случае сжимаемой жидкости и значение плотности.

Уравнению движения идеальной несжимаемой жидкости можно придать вид, отличный от уравнения Эйлера. Для этого формально преобразуем левую часть уравнения Эйлера.

Ускорение жидкости в проекции на ось х записывалось в уравнении Эйлера в виде

Добавлением и вычитанием величины этому выражению можно придать вид

.

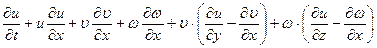Так как

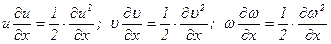
и

,

то левая часть уравнения Эйлера будет иметь вид

,

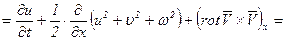
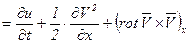где 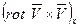- проекция векторного произведения двух векторов на ось x.

Преобразуя аналогично остальные уравнения Эйлера, запишем уравнения движения идеальной жидкости в форме Громека

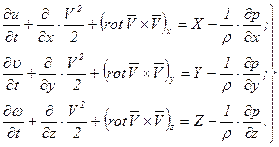(7.5)

Предположим, что массовые силы, проекции которых на оси координат обозначены через X, Y и Z, имеют потенциал, т.е. что существует такая функция координат U, которая удовлетворяет следующим условиям

или

.

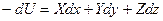Это предположение можно сделать потому, что в практике массовой силой большей частью является сила тяжести, а сила тяжести, как известно, имеет потенциал.

Тогда, считая 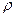постоянной величиной, уравнения (7.5) можно записать в виде

;

;

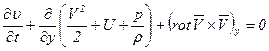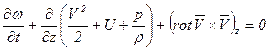
или в векторном виде

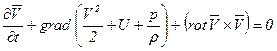. (7.6)

Уравнение (7.6), так же как и уравнение (7.5), называется уравнением Эйлера в форме Громека. Граничные и начальные условия для этих уравнений будут такими же, как и для уравнения Эйлера. Особенность уравнения Эйлера в форме Громека заключается в выделении в явном виде члена, содержащего вихрь вектора скорости.

При равенстве нулю слагаемого система уравнений (7.5) сильно упрощается и нетрудно получить интеграл этого уравнения. Последнее слагаемое обращается в нуль в трех случаях: 1) скорость потока равна нулю; 2) векторы скорости и вихря скорости параллельны и поэтому векторное произведение равно нулю. Это случай так называемого винтового движения, весьма редко встречающегося в практике; 3) вихрь скорости равен нулю. Это - безвихревой или так называемый потенциальный поток.

7.2. Интегралы уравнения движения жидкости для разных

случаев движения. Баротропные и бароклинные течения

Если во всей области движения 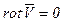, то существует потенциал скорости 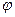, т.е. по формуле (3.55)

(7.7)

или

.

Тогда уравнение Эйлера в форме Громека (7.6) примет вид

.

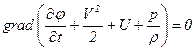Следовательно, выражение в скобках может зависеть только от времени, а от координат не зависит. Интеграл этого уравнения будет

,

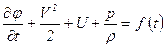где 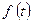определяется из граничных условий. Этот интеграл уравнения Эйлера называется интегралом Коши для потенциального движения идеальной несжимаемой жидкости.

Когда массовые силы являются только силами тяжести, потенциал этих сил принимает вид U = gz, а интеграл Коши

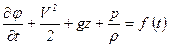. (7.8)

В уравнении (7.8) имеется два неизвестных 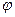и р, поэтому для решения задачи следует воспользоваться уравнением неразрывности

.

Подставляя в это уравнение значения проекций скорости по формуле (7.7), получим

. (7.9)

Уравнение (7.9) является уравнением Лапласа, решая которое можно найти 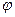. Подставив значение 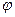в уравнение (7.8) и имея в виду, что

,

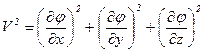определим давление р. Произвольная функция 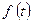будет найдена по величине р(t) в некоторой точке.

Если движение стационарно, т.е. 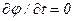, то уравнение (7.8) примет вид

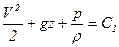. (7.10)

Этот интеграл уравнений Эйлера называется интегралом Бернулли для потенциального стационарного потока идеальной несжимаемой жидкости. Постоянная будет одной и той же для всей области потенциального потока. Этот интеграл, часто называемый уравнением Бернулли, имеет большое значение для всей гидромеханики. Из уравнения Бернулли видно, что во всей области безвихревого потока энергия жидкости в единице массы остается постоянной. Первое слагаемое выражения (7.10) является кинетической энергией, второе - потенциальной и третье - работой сил давления.

Умножив все слагаемые уравнения (7.10) на величину плотности, получим интеграл Бернулли в виде суммы слагаемых, имеющих размерность давления

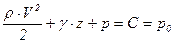, (7.11)

Дата добавления: 2014-01-06