Гидравлика 9 страница

где р - пьезометрический напор;

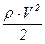- скоростной или динамический напор;

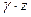- геометрический напор;

- полный напор.

В соответствии с уравнением (7.11) сумма динамического, пьезометрического и геометрического напоров во всей области потенциального потока остается величиной постоянной.

Разделив обе части уравнения (7.11) на g, получим уравнение Бернулли в виде

. (7.12)

Каждый член, входящий в уравнение (7.12), имеет размерность длины. Величину называют динамической высотой, - пьезометрической и z - геометрической высотой.

Согласно уравнению (7.12) сумма динамической, геометрической и пьезометрической высот во всей области потенциального потока остается величиной постоянной.

При отсутствии массовых сил интеграл Бернулли запишется в виде

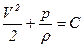(7.13)

или

.

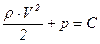Если в уравнении (7.11) скорость V будем считать равной нулю, то получим интеграл уравнения Эйлера для гидростатики .

Для того чтобы проинтегрировать уравнения Эйлера (7.2) вдоль линии тока, проделаем некоторые преобразования. Умножим уравнения (7.2) соответственно на dx, dy, dz

Затем, сложив почленно и разделив на 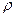, получим

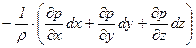. (7.14)

Отдельные слагаемые левой части уравнения, имея в виду стационарность потока, представим в виде

Уравнение (7.14) будет справедливо лишь на линии тока, если между элементами дуги и скоростью будут соблюдаться соотношения (3.13)

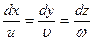
или

.

Используя последние равенства, получим

;

так как выражение в скобках представляет собой полный дифференциал. Окончательно левая часть уравнения (7.14) может быть представлена следующим образом

.

Тогда, полагая наличие потенциала массовых сил, уравнение (7.14) запишем в виде

или

. (7.15)

При постоянной плотности, что соответствует несжимаемой жидкости, получим

.

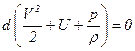Это уравнение можно легко проинтегрировать. Интегралом будет

или, имея в виду выражение потенциала сил тяжести, запишем

. (7.16)

Выражение (7.16) называется интегралом или уравнением Бернулли для линии тока.

Это уравнение получено при отсутствии предположения о потенциальности потока. Таким образом, выражение (7.16) справедливо также вдоль линии тока в случае вихревого движения. Уравнение (7.16) тождественно с уравнением Бернулли для потенциального потока. Различие состоит в том, что при потенциальном потоке постоянная С сохраняет свое значение для всей области потока, а при вихревом потоке каждая линия тока имеет свое значение постоянной С. Если все линии тока начинаются в области, в которой жидкость покоится или движется равномерно и прямолинейно, постоянная С будет одинакова для всех линий тока. В случае вихревого движения постоянная С сохраняет свое значение и вдоль вихревой линии.

Когда плотность жидкости не постоянна, вид интеграла Бернулли определяется зависимостью плотности жидкости от параметров потока. Наиболее простым с точки зрения математики является движение, при котором плотность есть функция только от давления. Жидкости, плотность которых есть функция давления, называются баротропными. Для баротропных жидкостей плотность равна

.

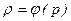Тогда уравнение (7.15) для стационарного потока при наличии потенциала массовых сил будет

.

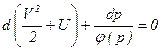Если ввести интеграл в виде

, (7.17)

то получим

или

.

Последнее выражение есть интеграл Бернулли для баротропного движения.

Интеграл Бернулли для одномерного баротропного движения при отсутствии массовых сил имеет вид

,

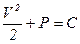где Р - так называемая функция давления, значение которой определяется из выражения (7.17) при заданной связи между плотностью и давлением.

Для изотермического процесса функция давления равна

,

следовательно, интеграл Бернулли будет иметь вид

. (7.18)

Приведенные в данном разделе уравнения интегралов Бернулли далеко не исчерпывают всех возможных его видов, но указанных форм вполне достаточно для понимания изложения последующего материала.

Интеграл Бернулли является одним из основных уравнений гидравлики (механики жидкости и газа) и широко применяется в различных своих формах.

8. ОБЩАЯ ИНТЕГРАЛЬНАЯ ФОРМА УРАВНЕНИЙ КОЛИЧЕСТВА ДВИЖЕНИЯ И МОМЕНТА

КОЛИЧЕСТВА ДВИЖЕНИЯ

8.1. Законы сохранения

На движение сплошных сред распространяются общие законы природы. Среди этих законов особенно важное и наиболее общее значение имеют законы сохранения. В механике обычно рассматриваются законы сохранения четырех величин: массы, количества движения, момента количества движения и энергии.

Все законы сохранения относятся к так называемым изолированным системам. Будем в дальнейшем называть систему изолированной или замкнутой в том случае, если через контрольную поверхность - окружающую систему - нет переноса массы, количества движения и энергии. На изолированную систему не действуют внешние силы.

Количество движения системы материальных точек, как известно из теоретической механики, есть векторная величина, равная произведению массы системы на скорость ее центра инерции.

Закон сохранения массы для изолированной системы выражается в том, что масса m такой системы остается постоянной во все время движения, т.е. количество вещества остается постоянным или

. (8.1)

Закон сохранения количества движения утверждает, что при движении изолированной системы общее количество движения остается постоянным во все время движения, т.е.

. (8.2)

Так как 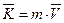(m - масса данной системы, а - скорость ее центра инерции), то

.

Но по закону сохранения массы для данной системы
m = const, поэтому

.

Отсюда видно, что ускорение центра инерции изолированной системы равно нулю

.

Если изолированная система состоит из отдельных частей, то

,

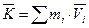где 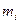- массы отдельных частей данной системы;

- скорости их центров инерции.

При 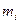= const, имеем

или

.

Отсюда следует, что если одна часть системы с массой 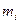получила некоторое изменение скорости дивижения , то остальные части изолированной системы должны изменить свои скорости так, чтобы выполнялось последнее равенство.

Закон сохранения момента количества движения утверждает, что при движении изолированной системы момент количества движения системы относительно некоторой точки, равный

,

где - радиус-вектор центра инерции части системы с массой ;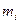

- скорость центра инерции этой части,

остается постоянным во все время движения, т.е.

, (8.3)

так как

.

Отсюда следует, что если внутри изолированной неподвижной системы в некоторый момент времени часть системы придет в движение, то остальная часть системы должна прийти в такое движение, чтобы общий момент количества движения оставался равным нулю.

Закон сохранения энергии гласит, что сумма всех видов энергии Е в изолированной или замкнутой системе остается во все время движения величиной постоянной, т.е.

. (8.4)

8.2. Закон изменения количества движения

Из курсов физики и теоретической механики известна теорема об изменении количеств движения, согласно которой производная по времени от главного вектора количеств движения массы, заключенной в некотором объеме , равна главному вектору всех внешних сил , приложенных к объему

. (8.5)

Рассмотрим применение этой теоремы к стационарно движущемуся потоку жидкости.

Когда количество движения жидкости в объеме , заключенном внутри некоторой неподвижной (так называемой контрольной) поверхности s, будет равно

.

Подставив значение 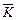в уравнение (8.5), получим

.

Так как, согласно закону о сохранении массы в течение всего времени масса частиц жидкости остается постоянной, т.е. , то предыдущее равенство запишется следующим образом

или в проекциях на оси координат

;

;

.

Сделаем далее преобразования лишь для проекции на ось х. Так как для стационарного движения 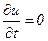и

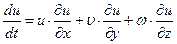
а

;

;

.

то

Очевидно, что второй интеграл в правой части обращается в нуль, так как при стационарном движении сжимаемой жидкости .

Пользуясь формулой Остроградского - Гаусса для связи интегралов по поверхности s и по объему , заключенному в этой поверхности, в форме

,

получим выражение изменения количества движения в проекции на ось х в виде

где

есть проекция вектора скорости на нормаль к площадке ds и, следовательно, есть масса жидкости, проходящая через элементарную площадку контрольной поверхности s.

Проделав аналогичные операции с проекциями на оси у и z, получим

;

.

Следовательно, уравнение импульсов или закон изменения количеств движения для стационарного движения любых жидкостей и всех сплошных сред (мука, пыль, песок и пр.) можно представить в векторной форме в следующем виде

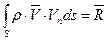. (8.6)

Можно заметить, что полученный закон изменения количеств движения для сплошных сред существенно отличается от ранее приведенной его формулировки для твердого тела. Это отличие выражается в том, что вместо производной по времени от количества движения некоторого твердого тела с объемом для сплошной среды рассматривается так называемый перенос количества движения через замкнутую контрольную поверхность s. Причем для определения изменения количеств движения некоторой массы жидкости, заключенной внутри контрольной поверхности, достаточно изучить только то, что происходит на этой контрольной поверхности.

8.3. Закон изменения момента количества движения

Для системы частиц закон об изменении момента количеств движения формулируется следующим образом: производная по времени от вектора главного момента количеств движения системы относительно какого-либо центра равна вектору главного момента внешних сил, приложенных к системе, взятому относительно того же центра, т.е.

. (8.7)

Если применить этот закон для объема жидкости 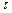, ограниченного контрольной поверхностью s, то получим, что изменение момента количеств движения 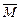относительно некоторой точки будет

.

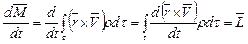После преобразований, аналогичных рассмотренным в предыдущем разделе 8.2, окончательно получим

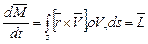. (8.8)

Следовательно, действие моментов внешних сил определяется моментом количеств движения жидкости, переносимым через поверхность s.

Еще раз подчеркнем, что применение законов об изменении количеств и момента количеств движения к объему, ограниченному некоторой контрольной поверхностью, не требует знания того, что происходит внутри выбранного объема. Необходимы знания величин лишь на поверхности s.

8.4. Силовое воздействие потока на ограничивающие

его стенки

В некоторых случаях в гидравлике удобно применять уравнения количества движения (импульса сил), например, когда надо найти силу воздействия потока на преграду или русло, не рассматривая процессы, происходящие внутри потока жидкости.

Для материального тела массой m, движущегося со скоростью , изменение количества движения за время dt вследствие действия силы 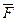выразится векторным уравнением

, (8.9)

где - приращение количества движения, обусловленное импульсом .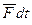

Применим эту теорему механики к участку потока с расходом Q между сечениями 1-1 и 2-2 в условиях установившегося течения (рис. 8.1).

Рис. 8.1. Схема применения уравнения количества

движения к жидкости

За время dt этот участок переместится в положение, определяемое сечениями 1'-1' и 2'-2'. Чтобы выразить приращение количества движения рассматриваемого участка, нужно из количества движения объема между сечениями 1-1 и 2-2 вычесть количество движения объема между сечениями 1’-1’ и 2'-2'. При вычитании количество движения промежуточного объема, ограниченного сечениями 1'-1’ и 2-2, сократится и останется лишь разность количеств движения элементов 2-2' и 1-1', которые на рис. 8.1 заштрихованы. Объемы этих элементов , а следовательно, и их массы одинаковы, поэтому приращение количества движения будет равно .

Это приращение количества движения обусловлено импульсом всех внешних сил, действующих на объем жидкости между сечениями 1-1 и 2-2, - сил давления в первом и втором сечениях и , силы тяжести всего объема G, а также реакции стенок русла R, которая складывается из сил давления и трения, распределенных по боковой поверхности объема. Обозначим вектор равнодействующих всех сил через 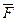. Тогда

,

или после сокращения на dt

. (8.10)

Таким образом, при установившемся движении вектор равнодействующей всех внешних сил, действующих на жидкость в фиксированном объеме, равен геометрической разности количеств движения жидкости, вытекающей из этого объема и втекающей в него за единицу времени. В этом заключается теорема Эйлера об изменении количества движения жидкого объема.

Уравнение (8.10) можно записать в виде

(8.11)

и в соответствии с этим построить замкнутый треугольник (или многоугольник) векторов, как показано на рис. 8.1. В связи с тем что в уравнении (8.11) вектор , имеет знак «минус», при построении он направлен в сторону, обратную действительному его направлению. То же уравнение (8.11) можно записать и в проекциях на ту или иную ось.

В качестве примера определим силу воздействия потока жидкости на преграду. Пусть жидкость вытекает в атмосферу и наталкивается на безграничную стенку, установленную нормально к потоку. В результате жидкость растекается по стенке, изменяя направление своего течения на 90° (рис. 8.2). Известны площадь сечения потока S, скорость истечения и плотность жидкости .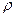

Рис. 8.2. Воздействие струи на преграду

Для решения данной задачи берем фиксированный объем, показанный штриховой линией, и применяем теорему Эйлера. Так как давление внутри струи и по поверхности жидкости равно атмосферному, т.е. избыточное давление равно нулю, уравнение, выражающее теорему Эйлера, для направления, совпадающего с вектором скорости истечения , будет иметь вид

. (8.12)

Это и есть сила воздействия потока жидкости на преграду. При другом угле установки стенки или других ее форме и размерах в правую часть формулы (8.12) вводится безразмерный коэффициент, отличный от единицы, но пропорциональность силы F произведению сохраняется.

ЗАКЛЮЧЕНИЕ

Данное учебное пособие содержит сведения о физическом строении и основных физических свойствах жидкостей и газов, наиболее распространенных моделях их представления и описания. Применительно к жидкостям и газам рассмотрены основы кинематики сплошных сред, общие законы и уравнения статики и динамики, а также их применение к различным частным случаям движения и покоя.

Последовательное изложение учебного материала должно способствовать глубокому усвоению студентами дисциплины «Гидравлика (механика жидкости и газа)». Применение основных физических закономерностей к частным случаям движения жидкостей и газов позволяет на конкретных примерах наиболее подробно изучить их специфические особенности.

Данная работа не охватывает всего курса дисциплины «Гидравлика (механика жидкости и газа)» и предназначена для восполнения имеющегося пробела в методической литературе, связанного с необходимостью системного изложения учебного материала в соответствии с требованиями Государственного образовательного стандарта высшего профессионального образования и примерной программы дисциплины, рекомендуемой министерством образования Российской Федерации для направления подготовки 151000 «Конструкторско- технологическое обеспечение автоматизированных машиностроительных производств», специальности 15100165 «Технология машиностроения».

БИБЛИОГРАФИЧЕСКИЙ СПИСОК

1. Башта Т.М., Руднев С.С., Некрасов Б.Б. и др. Учебник. Гидравлика, гидромашины и гидроприводы. - М.: Машиностроение, 1982. 423 с.

2. Лойцянский Л.Г. Механика жидкости и газа. Учебник - М.: Наука, 1987. 840 с.

3. Емцев Б.Т. Техническая гидромеханика. Учебник - М.: Машиностроение, 1987. 460 с.

4. Повх И.Л. Техническая гидромеханика. М. - Л.: Машиностроение, 1964. 508 с.

5. Знаменский В.А. Течения неньютоновских жидкостей: Учеб. пособие. Воронеж, ВГУ, 1980. 56 с.

6. Андерсон Д., Таннехил Дж., Плетчер Р. Вычислительная гидромеханика и теплообмен: В 2-х т. Пер. с англ. - М.: Мир, 1990. 384 с.

7. Флетчер К. Вычислительные методы в динамике жидкостей: В 2-х т. Пер. с англ. - М.: Мир, 1991. 504 с.

8. Тепло- и массообмен. Теплотехнический эксперимент: Справочник / Е.В. Аметистов, В.А. Григорьев, Б.Т. Емцев и др.; Под общ ред. В.А. Григорьева и В.М. Зорина. - М.: Энергоиздат, 1982. 512 с.

ОГЛАВЛЕНИЕ

Введение
1. Вводные сведения
1.1. Предмет механики жидкости и газа
1.2. Краткие исторические сведения о развитии науки
2. Основные физические свойства жидкостей и газов
2.1. Физическое строение жидкостей и газов
2.2. Основные физические свойства: сжимаемость, текучесть, вязкость, теплоемкость, теплопро- водность
2.3. Гипотеза сплошности
2.4. Два режима движения жидкостей и газов
2.5. Неньютоновские жидкости
2.6. Термические уравнения состояния
2.7. Растворимости газов в жидкостях, кипение, ка- витация. Смеси
2.8. Законы переноса
2.9. Требования к рабочим жидкостям
3. Основы кинематики сплошных сред
3.1. Два метода описания движения жидкостей и газов
3.2. Понятие о линиях и трубках тока. Ускорение жидкой частицы
3.3. Расход элементарной струйки и расход через поверхность
3.4. Уравнение неразрывности (сплошности)
3.5. Вихревое и безвихревое (потенциальное) движения
4. Силы, действующие в жидкостях
4.1. Массовые и поверхностные силы
4.2. Напряжения поверхностных сил
4.3. Напряженное состояние
5. Общие законы и уравнения статики и динамики жидкостей и газов
5.1. Уравнения движения в напряжениях

5.2. Уравнения гидростатики в форме Эйлера и их интегралы
5.3. Напряжения сил вязкости, обобщенная гипо- теза Ньютона
5.4. Уравнение Навье-Стокса для вязкой жидкости
5.5. Примеры аналитических решений уравнений Навье-Стокса для ламинарного движения в ци- линдрических трубах
6. Абсолютный и относительный покой (равновесие) жидких сред
6.1. Основная формула гидростатики
6.2. Определение сил давления покоящейся среды на плоские и криволинейные стенки
6.3. Относительный покой (равновесие) жидкости
7. Модель идеальной (невязкой) жидкости
7.1. Модель идеальной (невязкой) жидкости. Урав- нения Эйлера
7.2. Баротропные и бароклинные течения. Интегра- лы уравнения движения жидкости для разных случаев движения
8. Общая интегральная форма уравнений количества движения и момента количества движения
8.1. Законы сохранения
8.2. Закон изменения количества движения
8.3. Закон изменения момента количества движения
8.4. Силовое воздействие потока на ограничиваю- щие его стенки
Заключение
Библиографический список

Дата добавления: 2014-01-06