Особенности инфекционной болезни

F M

5. Масса тела: 5. Момент инерции:

6. Импульс: 6. Момент импульса:

7. Второй закон Ньютона: 7. Основное уравнение

вращательного движения:

8.Закон изменения 8. Закон изменения

импульса: момента импульса:

9. Элементарная работа: 9. Элементарная работа:

10. Кинетическая энергия 10. Кинетическая энергия

поступательного движения: вращательного движения:

1.7. Элементы релятивистской механики

Принцип относительности движения был сформулирован в ме­ханике для инерциальных систем еще Галилеем. Считалось, что время во всех таких системах течет одинаково, т. е. выступает как абсолютная величина. Из этого вытекало, что инвариантными (т.е. неизменными) относительно преобразований Галилея были лишь законы механики, а законы оптики и электродинамики уже оказы­вались неинвариантными.

Положение тела (материаль­ной точки) определяется относительно какой-то выбранной системы отсчета, выбранной системы координат. Такую систему отсчета в принципе можно связать с любым телом и в том числе с Землей. При этом следует учитывать, движется ли сама выбранная система отсчета относительно других систем. Так вошли в рассмотрение инерциальные системы координат, инерциальные системы от­счета.

Под инерциальной системой отсчета в физике понимается та­кая система отсчета, в которой выполняется первый закон Ньютона, или закон инерции. Это означает, что в инерциальной системе от­счета любое тело, на которое не действуют внешние силы, или по­коится или движется с постоянной по величине и направлению ско­ростью. Другими словами, в инерциальной системе отсчета любая изолированная материальная точка (на нее не действуют силы) имеет ускорение, равное нулю.

Очевидно, что всякая система отсчета, которая движется прямолинейно и равномерно относительно инерциальной системы отсчета, также будет инерциальной системой. Последнее утверждение, как увидим дальше, можно доказать.

Связь между координатами одной и той же точки М в двух различных инерциальных системах координат определяется просто (рис. 7-1).

Рис. 7-1

Будем считать, что система О неподвижна, а система О движется относительно нее с постоянной скоростью v в направлении оси X. Координаты (y, x) и (y´, x´) в этих системах не изменяются, т.е. возможные повороты систем отсутствуют и

y´= y, z´ = z. (7.1)

При сделанных предположениях координаты вдоль осей х и х' произвольной точки М в этих системах будут связаны друг с другом простым соотношением:

x=x'+vt. (7.2)

Можно записать и обратный переход от координаты в системе О к координате в системе О':

х'=х-vt. (7.3)

По классической механике считалось, что время в обеих системах О и О' течет одинаково, т. е.:

t'=t. (7.4)

Таким образом, для выбранного случая движения вдоль оси x преобразования координат и времени в классической механике при переходе от подвижной системы отсчета к неподвижной будут следующими:

x=x'+vt; у=y'; z=z'; t=t'. (7.5)

Обратные преобразования координат и времени:

х'=х - vt; y'=у; z' = z; t'=t. (7.6)

Видно, что координаты и время точки в одной инерциальной системе отсчета связаны с координатами и временем этой же точки в другой инерциальной системе отсчета простой линейной зависимостью.

Если же в общем случае начало О' подвижной системы отсчета движется со скоростью v относительно начала О неподвижной системы в произвольном направлении (рис. 7-2),то для точки М получим:

r = r₀ + r', (7.7)

где r — радиус-вектор точки М в системе О; r' — радиус-вектор точки M в системе О', a r₀ = vt. Равенство (4.7) можно переписать и в другом виде:

r' = r – vt (7.7')

Рис. 7-2

Зная связь между координатами точки в двух инерциальных системах О и О', легко определить и зависимость между скоростями этой точки. Для этого, дифференцируя по времени выражение (7.7) получим:

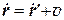
или:

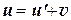. (7.8)

Закон сложения скоростей в классической механике также представляет собой линейную зависимость или линейное преобразование. Отсюда следует, что в классической механике относительная скорость остается инвариантной при переходе от одной инерциальной системы к другой.

Для ускорений, будем иметь:

, (7.9)

т.е. в инерциальных системах ускорение тела также одинаково или инвариантно. Из этого следует, что система, движущаяся с постоянной скоростью относительно инерциальной системы, также будет инерциальной. Поскольку в классической механике постулируется независимость массы тела от скорости его движения, то в рассматриваемых инерциальных системах отсчета О и О' масса должна быть одинаковой (инвариантной), т. е.

m' = m. (7.10)

Это означает, что будут равны силы:

m a ' = m a и F ' = F. (7.11)

Отсюда следует, что согласно классической механике второй закон Ньютона (т.е. основной закон динамики) будет инвариантным в инерциальных системах отсчета (инвариантным относительно преобразований Галилея). Это означает, что силы, действующие на тело в инерциальных системах О и О', будут одинаковыми. С этим положением на опыте столкнулся еще Галилей, изучавший механические движения тел (свободное падение, колебание маятника и др.) в закрытой каюте покоящегося и равномерно движущегося корабля.

Поэтому, принцип относительности Галилея формулируется следующим образом: никакими механическими опытами, выполнен­ными в данной системе отсчета, нельзя установить, покоится ли эта система или она движется равномерно, т. е. с постоянной скоростью.

Однако можно показать, что для законов электродинамики и оптики преобразования Галилея не инвариантны в инерциальных системах.

Вывод из этих противоречий был сделан в 1905 году Эйнштейном, предложившим специальную теорию относительности, как новое учение о пространстве и времени. Анализируя многочисленные экспериментальные данные, Эйнштейн пришел к заключению о том, что никакими физическими наблюдениями и опытами (механическими, оптическими и др.), проведенными в данной инерциальной системе отсчета, нельзя обнаружить ее равномерное и прямолинейное движение.

Другими словами, все законы физики, в том числе и законы электродинамики и оптики, должны быть инвариантными по отношению к инерциальным системам отсчета. Это предположение (постулат) считается основным в теории относительности Эйнштейна и называется принципом относительности.

Вторым постулатом специальной теории относительности является принцип постоянства скорости света в вакууме. Согласно этому принципу скорость света в вакууме не зависит от движения наблюдателей и источников и является величиной постоянной, равной: с =3.10⁸ м/с.

Этот второй постулат основан на опыте Майкельсона, которому не удалось обнаружить зависимость скорости света в вакууме от скорости движения источ­ника или наблюдателя.

Однако из этого следует, что закон сложения скоростей в классической механике противоречит второму постулату специальной теории относительности. На основе формулы (7.8) можно заключить, что, если в системе О' световой сигнал распространяется со скоростью с, то в системе О его скорость будет равна (с + v), что противоречит принципу постоянства скорости света в вакууме.

Новые формулы преобразования координат и времени для инерциальных систем отсчета, удовлетворяющие обоим постулатам теории относительности, были получены при условии, что время в этих системах течет неодинаково, т. е. что t' = t.

С учетом, что при движении вдоль оси х координаты у и z не изменяются, преобразования координат будут:

(7.12)

А для преобразования времени:

. (7.13)

Для обратного перехода от системы О' к системе О:

. (7.14)

(7.15)

Эти выражения называются преобразованиями Лоренца. Легко показать, что в случае медленного движения тел или частиц, когда v<<c, преобразования Лоренца переходят в преобразования Галилея:

(7.16)

и 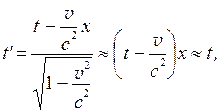(7.17)

Поэтому преобразования Лоренца в теории относительности справедливы для быстродвижущихся частиц или для частиц, движущихся со скоростью, близкой к скорости света. В случае же медленных или обычных механических движений они переходят в преобразования Галилея.

Из преобразований Лоренца выте­кают некоторые важные следствия.

Одновременность событий

Если в различных точках с координатами х ₁ и х ₂ неподвижной системы О (рис. 7-1) происходят одновременно (t ₂= t ₁) два события (например, вспышки света), то в подвижной системе О' эти события оказываются уже неодновременными.

. (7.18)

Иначе говоря, одновременность событий не сохраняется при переходе от одной системы отсчета к другой.

Интервал времени между двумя событиями

Если в системе О в данной точке (x ₂ - x ₁) происходят после­довательно два события, интервал времени между которыми равен:

D t = t ₂ -t ₁,

то интервал времени D t'=t ₂ ' - t ₁ ' между теми же событиями в системе О' можно записать при условии x ₂ - x ₁ = 0 следующим образом:

(7.19)

Следовательно, в движущейся системе координат интервал вре­мени между событиями удлиняется, становится больше по сравнению с интервалом времени между теми же событиями в неподвижной системе координат. Поэтому принято говорить, что в движущейся системе отсчета часы идут медленнее, чем в неподвижной системе отсчета, т. e. как бы имеет место «удлинение времени» для часов движущихся, по сравнению с часами, покоящимися или неподвижными.

Изменение длины при переходе к движущейся системе отсчета

Пусть в неподвижной системе отсчета О длина объекта, координаты концов которого x ₁ и x ₂, равна l = x ₂ - x ₁ =D x. При этом считается, что измерение координат происходит одновременно как в одной, так и в другой системах отсчета.

Значение интервала длины D x'=x ₂ ' - x ₁ ' = l' в подвижной системе О ' будет

, (7.20)

причем интервал времени D t=t ₂ - t ₁ определяется, считая, что координаты x ₂ ' и x ₁ ' в системе О' измерены одновременно (т.е. t ₂ ' - t ₁ ' =0). Следовательно

. (7.21)

и

, (7.22)

или:

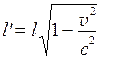. (7.23)

Таким образом, на основании преобразований координат и времени в специальной теории относительности можно заключить, что понятие одновременности событий, интервала длины и интервала времени есть поня­тия относительные, которыми можно воспользоваться только для данной системы отсчета. Необходимо заметить, что, установив изменчивость интервала времени и относительности событий, специальная теория относительности не нарушила причинно-следственную связь явлений.

Однако не следует забывать, что все выводы специальной тео­рии относительности справедливы лишь для инерциальных систем, а неинерциальные или ускоренно движущиеся системы описываются уже общей теорией относительности или теорией тяготения.

Поскольку закономерности специальной теории относительности сказываются лишь в случае движения тел (частиц) с большой скоростью v, сравнимой со скоростью с, а такими частицами, в основном, являются элементарные частицы, подобные электрону, то и механику теории относительности (релятивистскую [1] механику) можно считать механикой элементарных частиц.

Закон сложения скоростей в релятивистской механике

Если что скорость какого-то тела (материальной точки) в системе О задается вектором u с составляющими u _x, u _y, u _z, а в системе О вектором u с составляющими u _x ', u _y ', u _z ', то закон сложения продольных составляющих скоростей в релятивистской механике имеет вид

, (7.24)

а для поперечных составляющих

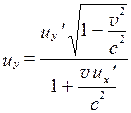. (7.25)

И аналогично для составляющих вдоль оси z:

(7.26)

,

Импульс и энергия в релятивистской механике

В классической механике Галилея — Ньютона второй закон Ньютона инвариантен в инерциальных системах отсчета. В соответствии с первым постулатом специальной теории относительности этот закон остается инвариантным и в релятивистской механике, если правильно определить импульс. Импульс тела (частицы) в релятивистской механике определяется по формуле

, (7.27)

где m ₀ - масса частицы, которая остается инвариантной во всех инерциальных системах отсчета (иногда ее называют массой покоя частицы). Для малых скоростей (v<<c) импульс принимает обычное выражение:

p =m ₀ v. (7.28)

Силу можно записать так:

, (7.29)

А энергия W частицы равна работе, затраченной на приобретение этой энергии. Поэтому:

. (7.30)

Дифференцируя правую часть выражения (7.30) по скорости, получим:

, (7.31)

Выражение для самой энергии W тела (частицы) получается путем интегрирования (7.31) и записывается в виде:

(7.32)

Если константу в (7.32), следуя Эйнштейну, положить равной нулю, то формула для энергии быстро движущейся частицы запишется так:

(7.33)

Из (7.33) следует, что при v =0 энергия частицы будет равна:

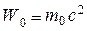, (7.34)

т.е. покоящаяся частица также обладает энергией, которую можно трактовать как некоторую внутреннюю энергию частицы (энергию покоя).

Если же (7.33) определяет энергию движущейся частицы, а (7.34) ее энергию покоя, то кинетическая энергия W _k частицы по смыслу должна быть равна разности этих энергий:

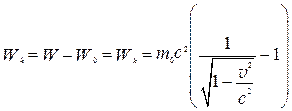, (7.35)

При малых скоростях движения формула (7.35) переходит в обычную формулу для кинетической энергии, известную из классической механики. В самом деле, при v<<c получим:

, т.е. .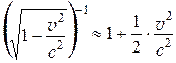

С учетом этого выражение (7.35) можно представить в виде:

, т.е. .

Кроме того, в релятивистской механике часто используется формула, непосредственно связывающая энергию и импульс частицы. Эта формула получается из (7.28) и (7.33) путем простой подстановки:

, (7.36)

откуда:

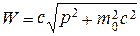. (7.37)

Если, например, предположить, что рассматриваемая частица - фотон, для которого масса покоя равна нулю (m₀ = 0), то из (7.37) получаем:

W=cp.

Кроме того,

W=hν,

где n - частота. Сравнивая эти два выражения, получим:

hν = cp, или ,

т.е. приходим к известной формуле, определяющей импульс фотона.

Формула взаимосвязи массы и энергии

Из (7.34) видно, что энергия покоя тела пропорциональна его массе, а величина с ² является постоянной. Отсюда следует, что изменения энергии покоя системы взаимодействующих тел (D W) и суммарной массы системы (D m) также будут пропорциональны друг другу:

D W= D mc ². (7.38)

Эта формула называется формулой взаимосвязи энергии и массы. Используя (7.38), всегда можно пересчитать изменение массы на изменение энергии и наоборот. Эта формула, как известно, имеет большое значение для атомной и ядерной физики, и она подтверждается на опыте.

Известно, например, что ядро атома гелия или (a-частица) состоит из двух протонов и двух нейтронов, однако их суммарная масса, больше, чем масса a-частицы. Это явление, при котором масса ядра меньше суммы масс составляющих его нуклонов, называется дефектом массы. Оказалось, что если этот известный из опыта «дефект массы» для ядра гелия пересчитать по формуле (7.38) на изменение энергии, то это изменение энергии будет соответствовать энергии связи нуклонов в таком ядре.

Точно так же известно, что при реакции деления ядра урана (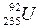) под воздействием медленных нейтронов суммарная масса продуктов деления оказывается меньше суммарной массы исходных продуктов на определенную величину D m. Если это изменение массы пересчитать по формуле (7.38) на изменение энергии D W, то получается энергия, которая и соответствует энергии связи (атомной энергии), которая выделяется при протекании данной реакции.

2. МОЛЕКУЛЯРНАЯ ФИЗИКА И ТЕРМОДИНАМИКА

2.1. Кинетические явления и теория идеальных газов

Молекулярная физика изучает строение и свойства вещества, исходя из молекулярно-кинетических представлений. По этим представлениям, любое тело (твердое, жидкое или газооб­разное) состоит из большого числа молекул или атомов, которые находятся в беспо­рядочном непрерывном движении.

Молекулярно-кинетическая теория объясняет свойства тел, которые наблюдаются на опыте (давление, температура и т. д.), как суммарный результат взаимодействия молекул. При этом если в механике изучалась простейшая форма движения - относительное перемещение тел, то в молекулярной физике изучается молекулярное движение, не сводимое к механическому. Для описания закономерностей молекулярного движе­ния используются методы статистической физики, описывающие не движение отдельных молекул, а лишь такие средние вели­чины, которые характеризуют движение огромной совокупности частиц. В зависимости от агрегатного состояния (газ, жидкость, твердое тело), вещество по-разному ведет себя при внешних воздействиях. Следовательно, при этом действуют межмолекулярные силы взаимного притяжения и отталкивания между частицами. Эти силы действуют на ничтожно малых расстояниях порядка двух-трех диаметров молекул и с увеличением расстояния убывают до нуля.

Таким образом, изучая свойства вещества, необходимо, кроме теплового хаотического движения, учитывать межмолекулярные силы.

В молекулярной физике рассматривается простейшая мо­дель - идеальный газ, т.е. совокупность материальных точек, не взаимодействующих между собой и обладающих лишь кинетической энергией.

Совокупность всех свойств тела называется состоянием тела. Величины, характеризующие состояние тела и изменяющиеся под влиянием внешних воздействий, называются параметрами состояния. Состояние данной мacсы идеального газа характеризуется тремя параметрами: объемом V, температурой Т и давлением р.

Если температура или давление в разных точках тела неодинаковы, то такое состояние называется неравновесным. Если тело предоставить самому себе и изолировать от других тел, то эти параметры выравниваются.

Состояние системы, при котором все параметры системы имеют определенные значения, остающиеся при изменении внешних условий постоянными сколь угодно долго, называется равновес­ным состоянием.

Связь между параметрами состояния устанавливается урав­нением состояния идеального газа, которое является обобщением опытных газовых законов Гей-Люссака и Бойля—Мариотта. Рассмот­рим процесс перехода газа из одного состояния в другое по схеме: сначала изотермический переход из состояния 1 в со­стояние 1', а затем изохорический переход из состояния 1' в со­стояние 2. В состоянии 1 параметры газа p₁, V₁, Т₁, в состоянии 2 - p₂, V₂, Т₂ (рис. 2-1-1).

Рис.2-1-1

Точки системы, находящейся в состояниях 1 и 1',лежат на одной и той же изотерме, и согласно закону Бойля—Мариотта:

. (2.1.1)

Точки, определяющие состояния 1' и 2, принадлежат одной изохоре:

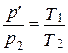. (2.1.2)

Исключая давление р', получим:

.

Обобщением этого является объединенный газовый закон Клапейрона:

. (2.1.3)

Согласно закону Авогадро грамм-молекулы всех газов занимают при одинаковых условиях (одинаковых температуре, давлении) один и тот же объем. Поэтому значение R для одного моля любого газа будет одинаково и называется универсальной газовой постоянной. Исходя из условий нормального состояния газа в системе СИ: р = 1,01·10 ⁵ Па; V_m= 22,4 ·10^-3 м³/моль; T = О°С=273 К, получается

.

Для произвольной массы идеального газа получается уравнение Менде­леева —Клапейрона:

. (2.1.4)

Основное уравнение молекулярно-кинетической теории газов устанавливает связь между макроскопическим параметром (давлением газа в сосуде) и микроскопическим параметром - средней кинетической энергией газовых молекул. Если считать столкновение молекул газа со стенками абсо­лютно упругим, то давление на стенки сосуда определится уда­рами частиц, отскакивающих от стенок без изменения величины скорости. Вследствие хаотичности движения частиц число уда­ряющихся частиц и их скорости будут различны в отдельные моменты времени. С молекулярно-кинетической точки зрения давление, оказываемое газом на стенки сосуда, представляет собой средний импульс силы от ударов молекул газа, приходя­щийся в единицу времени на единицу площади стенки.

Вывод уравнения приближенный и использует ряд допуще­ний:

1. Движение молекул газа происходит только в трех взаимно перпендикулярных направлениях.

2. В каждом из направлений движется 1/3 всех молекул.

3. При каждом ударе молекул газа о стенку они передают стенке импульс. При этом считается, что движение молекулы нормально к стенке и удар абсолютно упругий.

Строгий вывод показывает, что эти допущения компенсируют друг друга и результат в приближенном вы­воде получается правильный.

Тогда основное уравнение молекулярно-кинетической теории газов

(2.1.5)

устанавливает связь между макроскопическим параметром - давлением и микроско­пическим - средней кинетической энергией молекул газа.

Если преобразовать формулу основного уравнения, умножив левую и правую ее части на объем одного моля газа:

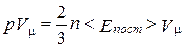. (2.1.6)

получим

, (2.1.7)

где nV_m=N_А. число частиц в одном моле, равное числу Авогадро. Отсюда

, (2.1.8)

где отношение 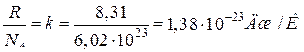представляет собой постоянную Больцмана. Выражение (2.1.8) можно переписать таким образом:

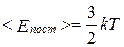, (2.1.9)

т. е. средняя кинетическая энергия поступательного движе­ния молекул идеального газа пропорциональна абсолютной тем­пературе.

Из формулы (2.1.9) ясен физический смысл абсолютной температуры: она является количественной мерой средней кинетической энергии поступательного движения молекул. При температуре, равной нулю, кинетическая энергия моле­кул также равна нулю. Однако это не означает, что прекращается всякое движе­ние молекул газа. При низких температурах элект­роны продолжают движение вокруг ядер. Таким образом, абсо­лютный нуль означает не отсутствие движения, а такое состоя­ние вещества, при котором дальнейшее уменьшение интенсив­ности движения вследствие отдачи его энергии окружающим телам невозможно. Поэтому, при низких температурах, когда уменьшается влияние теплового движения на процессы, протекающие в веществе, можно ожидать возникновения новых свойств и явлений (сверхпроводимость, сверхтекучесть).

Кинетическая энергия поступательного движения всех час­тиц N_A, содержащихся в одном моле газа, определится так:

, (2.1.10)

а для произвольной массы газа m, содержащей (m/m) молей:

. (2.1.11)

Из (2.1.5) и (2.1.9) получим:

, (2.1.12)

т. е. давление газа пропорционально его температуре.

Предположим, что имеется газовая смесь в единице объема, содержащая n₁ молекул одного газа, n₂ - второго, n₃ - треть­его и т.д. Всего имеется N типов молекул. Так, например, воздух состоит из молекул кислорода, азота, углекислого газа и т.д. Тогда общее число молекул в единице объема равно:

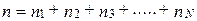. (2.1.13)

Из (2.1.12) и (2.1.13) получим закон Дальтона:

. (2.1.14)

Давление смеси идеальных газов равно сумме парциальных давлений газов, об­разующих смесь. Давления p₁, р₂,...р_N называются парциальными давлениями [2].

Внутренняя энергия системы

Внутренней энергией системы (например, некото­рой массы газа) называется кинетическая энергия хаотического движения молекул, потенциальная энергия взаимодействия между молекулами и внутримолекулярная энергия. При рассмотрении идеального газа пренебрегают потен­циальной энергией взаимодействия молекул и внутримолеку­лярной энергией, а под внутренней энергией идеального газа понимают суммарную кинетическую энергию теплового движе­ния его молекул.

Существенно, что внутренняя энергия является функцией состояния. Это означает, что внутренняя энергия системы, которая находится в данном состоянии, принимает присущее этому состоянию значение, независимо от того, что происходило в си­стеме ранее.

Следовательно, изменение внутренней энергии при переходе системы из одного состояния в другое будет всегда равно разности значений внутренней энергии в этих состояниях, независимо от пути, по которому совершается переход.

Средняя кинетическая энергия поступательного движения одной молекулы идеального газа, которую мы считали материальной точкой, равна 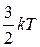, то есть, прямо пропорциональна температуре газа.

При рассмотрении двухатомных, трехатомных и многоатомных молекул, кроме поступательного движения следует учитывать также вра­щательное и колебательное движения молекул газа.

Для подсчета энергии, идущей на все виды движения, вво­дится понятие числа степеней свободы. Числом степеней свободы тела называется минимальное число независимых координат, которое необходимо задать для того, чтобы полностью определить положение тела в пространстве.

Модель молекулы одноатомного газа - материальная точка, для описания ее положения в пространстве задаются 3 коорди­наты, т.е. 3 степени свободы.

При рассмотрении модели молекулы двухатомного газа в виде двух жестко связанных материальных точек необходимо задать 3 координаты центра тяжести для описания поступательного движения и 2 степени свободы для описания вращательного движения относительно двух вза­имно перпендикулярных осей, не совпадающих с осью молекулы.

Для трехатомных и многоатомных жестких молекул, как и для твердого тела произвольной формы, общее число степеней свободы i =6; из них 3 степени свободы прихо­дятся на поступательное движение центра тяжести и 3 - на вращательное движение относительно осей х, у, z.

Если все виды движения равновероятны, и предполагая, что ни один из видов движения не имеет преимущества перед дру­гими, можно считать, что количество энергии, приходящееся на одну степень свободы равно

.

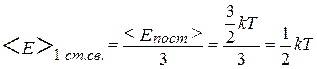Если молекула имеет i степеней свободы, то ее средняя энер­гия равна:

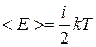. (2.1.15)

Внутренняя энергия идеального газа определяется как сум­марная кинетическая энергия всех его молекул. Для одного моля газа она равна:

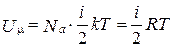, (2.1.16)

а для произвольной массы газа она равна:

. (2.1.17)

Теплоемкость газов

Для повыше­ния температуры тела, масса которого равна m, на величину Δ T необходимо затратить количество тепла:

D Q=cm D T, (2.1.18)

где с — удельная теплоемкость вещества.

Под удельной теплоемкостью подразумевают физическую величину, численно равную количеству тепла, которое необходимо сообщить веществу, масса которого равна единице для нагревания этого количества вещества на D T =1 К.

Для одного моля газа вводится молярная теплоемкость C_m.. Под молярной теплоемкостью подразумевается физическая величина, численно равная количеству тепла, кото­рое необходимо сообщить одному молю этого вещества, чтобы поднять его температуру на 1 К.

Для нагревания нескольких мо­лей газа на один Кельвин необходимое количество тепла будет равно:

. (2.1.19)

Соотношение между удельной и молярной теплоемкостями:

С_m=сm.. (2.1.20)

Величина теплоемкости газа зависит от условий, при кото­рых она измеряется. Нагрев может идти при постоянном объеме или при постоянном давлении, и при этом теплоемкости назы­ваются соответственно теплоемкостью при постоянном объеме C_V и теплоемкостью при постоянном давлении С_P.

Нагревание одного моля газа может происходить при различных условиях.

1. V =const. Если газ нагревается при постоянном объеме, то тепло, подводи­мое к газу, идет лишь на его нагревание, т. е. на увеличе­ние внутренней энергии, поскольку работа против действия внешних сил не производится:

.

Учитывая формулу (2.1.19), имеем:

. (2.1.21)

Если 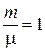, то:

. (2.1.22)

Учитывая, что:

, (2.1.23)

на основе (2.1.22) получим:

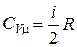; . (2.1.24)

Молярная теплоемкость газа при постоянном объеме опреде­ляется числом степеней свободы его молекул и газовой постоян­ной. По классической теории теплоемкость газа не зависит от температуры.

2) p =const. При нагревании газа при постоянном давлении этот газ расширяется. Сообщаемое ему тепло идет не только на увеличение его внутренней энергии, но и на совершение работы против сил внешнего давления. Таким образом, теплоемкость С_Pm должна быть выше теплоемкости C_Vm на величину, равную работе D A_m, кото­рую совершает один моль газа при расширении:

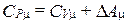. (2.1.25)

Рис. 2-1-2

Если нагревается 1 моль газа, находящийся при температуре Т и давлении р в цилиндре с поршнем, площадь которого равна S (рис. 2-1-2), то работа D A, которая совершается против действия сил внешнего давления при перемещении поршня на малое расстояние D l и при соответствующем увеличении объема газа на величину D V за счет подводимого тепла D Q_p определится так:

D A = F D l = pS D l=p D V. (2.1.26)

Из уравнения состояния иде­ального газа:

p D V_m = R D T, (2.1.27)

и (2.1.26):

D A =D A_m = R D T. (2.1.28)

Таким образом, при нагревании 1 моля газа при постоянном давлении на 1 Кельвин, работа численно равна универсальной газовой постоянной:

D A_m=R. (2.1.29)

Теперь из (2.1.25) получим:

C_pm=C_Vm+R. (2.1.30)

Отсюда

, (2.1.31)

. (2.1.32)

Из (2.1.31) и (2.1.32) получим отношение теплоемкостей при постоянном давлении и при постоянном объеме, характер­ное для каждого газа:

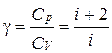. (2.1.33)

Это отношение является характеристикой газа и зависит только от числа степеней свободы молекул, из ко­торых состоит газ. Поэтому для различных по своему составу газов, но имеющих одинаковое число атомов в молекулах, это отношение одинаково. Так, например, молекулы двухатомных газов, таких, как кислород, водород, азот и т.д., имеют в составе одной молекулы два атома. Поэтому для всех этих газов .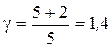

Для одноатомных газов, таких, как неон, аргон и т.д., .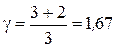

Адиабата идеального газа

Адиабатическим называется процесс, протекающий без теплообмена с окружающей средой. При адиабатическом процессе система не получает тепла извне и не отдает тепла окружаю­щим телам. Поэтому система должна быть окружена стенками, не проводящими тепло­. Так как это условие осуществить нельзя, то всякий реальный процесс может происходить лишь как приближенный к адиабатическому. Практически, близкими к адиабатическому оказываются процессы, протекающие настолько быстро, что обмен теплом с внешней средой не успевает про­изойти.

Адиабатический процесс выражается в том, что в законе сохранения энергии суммарное количество тепла, подводимое к газу, расходуется на нагрева­ние газа при постоянном объеме, т. е. на изменение внутренней энергии газа, и на работу по изменению объема. Так как величина под­водимого тепла равна нулю, то работа может производиться только за счет изменения внутренней энергии газа:

dU+dA =0,

т.e.

dA=-dU. (2.1.34)

Если газ совершает положительную работу, то его внутрен­няя энергия убывает. Если внешние силы совершают работу над газом, то его внутренняя энергия увеличивается.

Работа, совершаемая газом при расширении, как известно, равна:

dA=pdV, (2.1.35)

а изменение внутренней энергии одного моля идеального газа:

. (2.1.36)

Используя (2.1.34), получим

C_VmdT+pdV =0. (2.1.37)

Из уравнения состояния идеального газа ()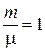

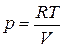
и (2.1.37) получим:

. (2.1.38)

Это выражение преобразуется так:

.

Или:

. (2.1.39)

Откуда следует:

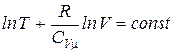. (2.1.40)

Рассмотрим коэффициент, стоящий перед lnV. Поскольку

,

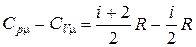то

. (2.1.41)

Тогда можно (2.1.40) переписать:

. (2.1.42)

Формула (2.1.42) представляет собой уравнение адиабатического процесса в переменных Т и V. Если в этой формуле выразить температуру Т из уравнения со­стояния идеального газа, то получим уравнение адиабаты в пе­ременных р и V или уравнение Пуассона:

PV ^g=const. (2.1.43)

Сравним изотермическое и адиабатическое изменения со­стояния газа. Для изотермического процесса характерно непре­рывное поступление тепла извне, которое полностью компенси­рует изменение внутренней энергии при совершении газом ра­боты. Т. е. изотермическое изменение объема газа возможно при идеально хорошем обмене теплом с внешними телами. Адиабатическое изменение объема возможно при идеально хо­рошей тепловой изоляции. Работа газа совершается за счет его внутренней энергии. При расширении газ охлаждается, при сжатии — нагревается. Уравнение изотермического процесса выражается законом Бойля—Мариотта:

pV =const, (2.1.43)

а формула (2.1.43) представляет собой уравнение адиабатического процесса. Если изобразить оба эти процесса графически, то кривая адиабаты пойдет круче, чем кривая изотермы (рис. 2-1-3). В точке M обе кривые пересекаются.

Рис. 2-1-3

Поскольку кривая изотермы соответствует процессу, проходящему при постоянной температуре, то адиабатическое расширение сопровождается понижением температуры, а адиабатическое сжатие - повышением температуры. Поэтому участок адиабаты выше точки M (т.е. при больших, чем в этой точке значениях объема) лежит ниже изотермы, а участок адиабаты, соответствующий значениям объема, меньшим, чем в точке M, лежит выше изотермы. На рис.2-1-4 представлены та же изотерма и две адиабаты - для двухатомного газа (g = 1,4) и для одноатомного газа (g = 1,67). Видно, что последняя адиабата идет круче первой.

Рис.2-1-4

Реальные процессы не носят строго изотермического или адиабатического характера, так как невозможно осуществить ни идеального обмена теплом, ни полной тепловой изоляции. Реальные процессы носят промежуточный характер между изо­термическим и адиабатическим.

2.2. Основы классической статистической физики

Законы механики, применяемые для систем частиц в условиях теплового равно­весия, получили название статистической ме­ханики. Одно из положений статистической механики известно. Это положение о том, что при некоторой температуре энергия, приходящаяся на каждую степень свободы, равна 1/2 kT.

Кроме того, из основного уравнения молекулярно-кинетической теории газов можно определить среднюю квадратичную скорость молекул газа:

, (2.2.44)

где m - масса одной молекулы газа, а m - молярная масса этого газа.

Таким образом, скорость молекул газа зависит от темпера­туры. Экспериментальное определение скоростей молекул было осуществлено в опыте Штерна.

Опыт показывает, что при каждом значении температуры Т существует наиболее вероятная скорость v_В, с которой движется большинство моле­кул. Молекулы, скорости которых много больше или много меньше наиболее вероятной, встречаются редко. Таким образом, суще­ствует некоторая статистическая закономерность распределения молекул по скоростям.

Впервые закон распределения молекул газа по скоростям (и по кинетическим энергиям) был получен Максвеллом на основе теории вероятности.

Вводя функцию распределения 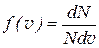, характеризующую относительное число молекул 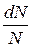, скорости которых ле­жат в заданном интервале от до + d , математически закон Максвелла можно записать так:

, (2.2.45)

где m - масса одной молекулы;

k - постоянная Больцмана;

T - абсолютная температура.

График функции распределения Максвелла показан на рис. 2-2-5.

Относительное число молекул 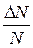, для которых значения скоростей находятся в заданном интервале от до (+D), численно равно площади прямоугольника, заштрихованного на рис. 2-2-5.

Рис.2-1-5

Скорость, соответствующая максимальному значению функ­ции распределения f (v), называется наиболее вероятной скоро­стью v _В. Её можно найти, если продифференцировать формулу (6.60) и приравнять полученную производную нулю:

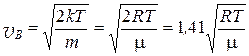. (2.2.46)

Закону Максвелла можно придать другой вид, если вместо скорости в качестве переменной взять кинетическую энергию 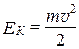. Тогда выражение

(2.1.47)

будет характеризовать функцию распределения молекул, значения кинетической энергии которых находятся в заданном интервале от 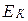до ().

Из выражений (2.2.45) - (2.2.47) следует, что вид функции распределения зависит от температуры и массы молекул.

С увеличением температуры максимум кривой функции распределения 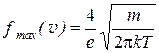смещается вправо и становится ниже. Это означает, что число быстрых молекул увеличивается, а медлен­ных—уменьшается, при этом площадь, ограниченная сверху кривой, не изменяется, так как число молекул не меняется.

Графики функции распределения молекул кислорода по их скоростям, рассчитанные по формуле (2.2.45), приведены на рис. 2-2-6.

Рис. 2-2-6

Три кривые, изображенные на рисунке 2-2-6, соответствуют трем различным температурам - 300, 600 и 900 К. По оси абсцисс отложены скорости молекул в м/c. Можно видеть, что наиболее вероятная скорость, соответствующая максимуму распределения, с ростом температуры увеличивается в соответствии с формулой (2.2.46).

Больцман обобщил закон Максвелла на случай, когда моле­кулы движутся в поле силы тяжести (в общем случае - в лю­бом силовом поле). При этом кинетическую энергию в формуле (2.2.47) следует заменить на полную энергию молекул Е=Е_K+Е_P, где Е_P - потенциальная энергия. Так как потенциальная энергия зависит от координат, то приходится говорить о числе молекул, для которых ограничены не только скорости опреде­ленным интервалом скоростей, но и координаты которых также ограничены определенным интервалом.

Окончательно закон рас­пределения Максвелла — Больцмана имеет вид:

. (2.2.48)

Существенно, что законы Максвелла и Больцмана справед­ливы для равновесного состояния идеального газа и выполня­ются тем точнее, чем больше число молекул N.

2.3. Реальные газы. Уравнение Ван-дер-Ваальса

Идеальный газ, для которого нами рассмотрены основные законы, представляет собой совокупность невзаимодействующих молекул. Эта модель может быть принята и для реальных раз­реженных газов. С повышением давления свойства реальных газов начинают отличаться от свойств идеальных газов.

Причина отличия свойств заключается в существовании сил отталкивания и притяжения между молекулами. Силы отталки­вания возникают в связи с тем, что газовые молекулы имеют конечные размеры. Силы притяжения между молекулами вызы­вают изменение давления газа в сосуде. Эти силы были уч­тены Ван-дер-Ваальсом при выводе уравнения реального газа. Рассмотрим действие этих сил.

Сила отталкивания

Молекулы газа, имеющие различные кинетические энергии, не могут сблизиться на расстояние, меньшее эффективного диа­метра молекул. Поэтому часть объема оказывается недоступной для молекул газа. Эту недоступную часть объема нужно вы­честь из общего объема сосуда. Обозначим эту часть объема через b и запишем уравнение состояния для одного моля газа с поправкой на этот объем:

p(V_m-b)=RT. (2.3.49)

Расчет показывает, что величина b равна учетверенному объему газо­вых молекул, содержащихся в одном моле. Размерность b равна размерности объема.

Сила притяжения

Сила взаимного притяжения между молекулами приводит к ослабле­нию интенсивности давления на стенки сосуда. Поэтому давле­ние реального газа следует уменьшить на величину р'. С учетом формулы (2.3.49) получим:

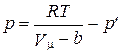. (2.3.50)

Для расчета можно воспользоваться следующими рассужде­ниями. Давление газа определяется концентрацией частиц n в прилегающем к стенке слое газа. Сила притяжения со стороны соседнего слоя, рассчитанная на единицу площади, пропорцио­нальна концентрации молекул в обоих слоях ~ n ², т. е. пропор­циональна квадрату плотности газа или обратно пропорцио­нальна квадрату объема газа:

.

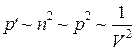Вводя коэффициент пропорциональности для одного моля, запи­шем:

, (2.3.51)

где а - коэффициент, зависящий от природы газа.

Таким образом, уравнение, полученное Ван-дер-Ваальсом для одного моля реального газа, имеет вид:

. (2.3.52)

Если под р понимать внешнее давление, оказываемое на газ, то p' добавляется к внешнему давлению, т. е. газ как бы оказы­вается дополнительно сжатым. Для произвольной массы газа уравнение Ван-дер-Ваальса получается путем обобщения выражения (2.3.52), если это уравнение умножить на число молей 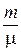. Следует также учесть, что 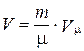. Тогда получим:

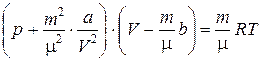. (2.3.53)

Это и есть уравнение Ван-дер-Ваальса. Отметим, что это уравнение нельзя считать абсо­лютно точным, так как отсутствует способ точного определения сил взаимодействия между молекулами газа.

Изотермы реальных газов

Уравнение Ван-дер-Ваальса (2.3.53) является кубическим (т.е. уравнением третьей степени) относительно объема. Поэтому, в отличие от изотермы идеального газа, имеющей вид гиперболы, изотерма Ван-дер-Ваальса, т.е. кривая, соответствующая уравнению (2.3.53), имеет области с максимумом и минимумом, где каждому значению давления соответствуют три значения объема. Эта изотерма представляет собой, по существу, графическое решение урав­нения (2.3.53).

Семейство таких изотерм, рассчитанных по уравнению (2.3.53) для углекислого газа, находящегося при различных температурах, представлено на рис.2-3-7. Из этого графика видно, что действительно, имеется некоторая область, в которой одному значению давления соответствуют три значения объема. В этой области находятся изотермы, рассчитанные для температур 250, 270 и 290 К.

Однако, уже при 310 К изотерма имеет лишь точку перегиба, но не имеет трех корней. Эта изотерма критическая и точка перегиба К называется критической точкой. Температура критической изотермы также называется критической температурой Т_К. Все изотермы, находящиеся выше критической, перегибов не имеют и приближаются к изотермам идеального газа, описываемым обычным уравнением Клапейрона.

Для всех температур ниже критической на изотермах, построенных по уравнению Ван-дер-Ваальса, изгиб выражен тем резче, чем ниже температура.

Однако, экспериментальные изотермы отличаются от изотерм, представленных на рис. 2-3-7. Противоречие между теоретическими и экспериментальными кривыми заключается в том, что последние вместо волнового изгиба имеют прямолинейный участок (рис.2-3-8).

Действительно, в реальности не может такого быть, чтобы при одном и том же давлении вещество находилось при нескольких объемах. Что же происходит при температурах ниже критической?

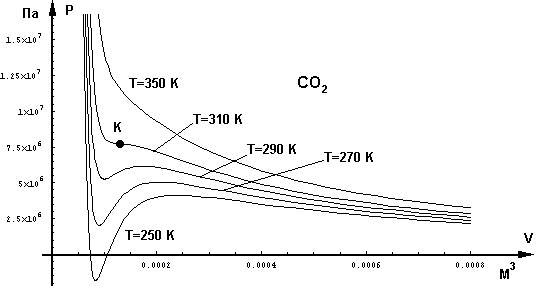
Рис.2-3-7

Горизонтальный участок изотермы b - d является областью фазового перехода, областью, в которой насыщенный пар находится в равновесии с жидкостью, и постепенно, по мере уменьшения объема переходит в жидкую фазу. То есть, в этой области реальные изотермы совпадают с изобарами, и фазовый переход из газообразного состояния в жидкое происходит при постоянном давлении. Выше области фазового перехода, на участке е-d, мы имеем газ, сжимаемый легко - кривая идет полого. Ниже области фазового перехода, на участке b-a, кривая идет очень круто, что соответствует трудно сжимаемой жидкости.

Изгиб теоретической изотермы на участке b - d определяет неустойчивые, так называемые метастабильные состояния. Эти метастабильные состояния действительно существуют. В точке d газ превращается в насыщенный пар. Состояние, которое характеризуется участком изотермы слева от точки d, отличается от насыщенного пара повышенной плотностью и повышенным давлением. Здесь мы имеем пересыщенный пар.

Увеличение жидкой фазы происходит путем конденсации насыщенного пара вокруг центров конденсации. Центрами конденсации могут служить мельчайшие капельки жидкой фазы или примеси в виде микроскопических пылинок или ионизированных молекул газа.

Прямой участок экспериментальной изотермы располагается таким образом, что заштрихованные площади ниже участка b - c и выше участка c - d равны друг другу.

Рис. 2-3-8

Для сравнения на графике приведена изотерма идеального газа, соответствующая этой же температуре.

Из рис. 2-3-8 видно, что при температурах, выше критической, фазовый переход происходить не может - при любом сжатии газа он в жидкость не переходит. В этих условиях изотермы реального газа мало отличаются от изотерм идеального газа.

2.4. Основы термодинамики

Первое начало термодинамики фактически является зако­ном сохранения энергии применительно к тепловым процессам.

Тепло, подводимое к системе, расходуется на увеличение её внутренней энергии и на совершение работы над внешними те­лами.

. (2.4.1)

Выражение (2.4.1) представляет собой формулировку первого начала. Рассмот­рим различные изопроцессы (т.е. процессы, протекающие при постоянстве какого-либо параметра) в идеальном газе и определим работу, которая совершается в этих процессах.

1. Изохорический процесс (dV=0)

Изохорическим называется процесс, протекающий при постоянном объеме. Тепло, подводимое к газу, целиком расходуется на нагревание газа в замкнутом объеме. Работа при изохорическом процессе будет равна нулю. Действительно,

dA=pdV= 0, (2.4.2)

поэтому все подводимое к газу тепло, идет на изменение его внутренней энергии.

dQ=dU;

dU=c_VmdT. (2.4.3)

Итак, при изохорическом процессе газ не совершает работы над внешними телами. Это иллюстрирует рис. 2-4-1. Изохорическому процессу соответствует прямая 3-4.

2. Изобарический процесс (dp=0)

Изобарическим называется процесс, протекающий при постоянном давлении. Работа при расширении газа отлична от нуля:

dA=pdV.

В этом случае первое начало термодинамики имеет вид:

dQ=dU+pdV. (2.4.4)

Следовательно, при изобарическом процессе подводимое к газу тепло затрачивается как на увеличение его внутренней энергии, так и на работу по расширению газа. Определим работу, совершаемую при изобарическом процессе.

dA=pdV; A=p (V₂ - V₁). (2.4.5)

Работу можно определить графически (рис.2-4-1).

Рис. 2-4-1

При изобарическом процессе газ расширяется от объема V₁ до объема V₂ и работа численно равна площади заштрихованного прямоугольника.

3. Изотермический процесс (dT=0)

Изменение внутренней энергии газа пропорционально измене­нию температуры, следовательно, в этом процессе внутренняя энергия газа остается постоянной. Поэтому первое начало термодинамики запишется так:

dQ=dA. (2.4.6)

Следовательно, при изотермическом процессе все подводимое к системе тепло затрачивается на работу по расширению газа. Изотермический процесс протекает согласно закону Бойля-Мариотта, т. е. .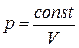

Графически этот процесс представляется гиперболой (рис.2-4-2). Определим работу А в изотермическом процессе:

. (2.4.7)

Выразим давление р из уравнения Менделеева—Клапейрона:

.
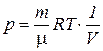