Определение числового ряда. Сходимость рядов, свойства сходящихся рядов. Необходимый признак сходимости числового ряда

Определение знакопеременного ряда. Знакочередующиеся ряды. Признак Лейбница. Абсолютная и условная сходимости рядов.

Ряды с положительными членами. Достаточные признаки сходимости положительных рядов (принцип сравнения, радикальный признак Коши, признак Даламбера). Интегральный признак Коши-Маклорена.

Определение числового ряда. Сходимость рядов, свойства сходящихся рядов. Необходимый признак сходимости числового ряда.

Определение. Пусть дана числовая последовательность 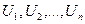,... Выражение вида (1) 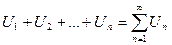называется числовым рядом. Числа 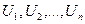называются членами ряда, число 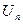– общий член ряда. Суммы конечного числа первых членов ряда 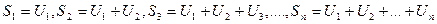называются частичными суммами ряда.

Так как число членов ряда бесконечно, то частные суммы образуют числовую последовательность .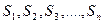

Определение. Если предел последовательности частичных сумм ряда существует и конечен, то ряд (1) называется сходящимся и сумма 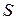ряда (1) равна пределу 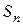: . Если предел не существует или бесконечен, то ряд называется расходящимся.

Примеры. Знакомые нами числа 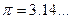и 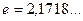означают, что .

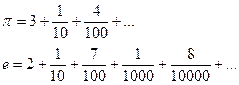По аналогии, любое десятичное разложение действительного числа представляет собой сходящийся числовой ряд, а частичные суммы 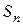– это приближенные значения числа с заданной точностью.

Рассмотрим бесконечную геометрическую прогрессию 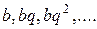, члены которой являются членами ряда 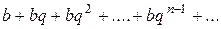. Частичная сумма этого ряда при 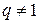имеет вид 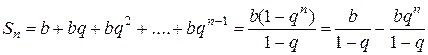. Отсюда: = =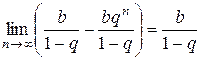, т.е. ряд сходится при и его сумма .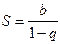

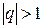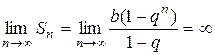При , то и ряд расходится.

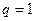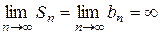Если , то и ряд расходится. При 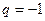ряд принимает вид 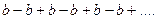. Частичные суммы ряда выглядят следующим образом 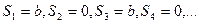. Последовательность частичных сумм ряда 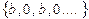предела не имеет и ряд расходится.

То есть при 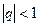ряд сходится, при 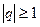– расходится.

Рассмотрим ряд 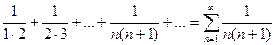. Зная, что 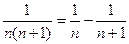имеем 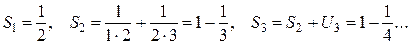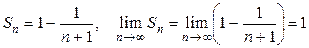. Так как существует и конечен, то ряд сходится и его сумма равна единице.

Свойства сходящихся рядов.

Если сходится ряд (1), то сходится и каждый ряд, полученный из него прибавлением или отбрасыванием конечного числа членов.

Над сходящимися рядами можно выполнять обычные арифметические действия, то есть если ряд 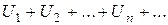сходится и его сумма равна S, и 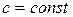, то сходится ряд 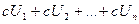и его сумма равна cS.

Пусть даны два ряда 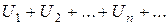и 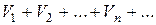. Если оба ряда сходятся, а их суммы равны соответственно S и T, то сходится ряд 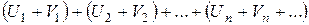и его сумма равна S+T.

Если сходится ряд (1), то сходится и каждый ряд, полученный из него группировкой слагаемых, причем суммы обоих рядов одинаковы.

При рассмотрении рядов возникают задачи: исследовать ряд на сходимость и, если он сходится, найти его сумму. В связи с этим существуют признаки сходящихся рядов.

Теорема (необходимый признак сходимости). Если ряд сходится, то предел его общего члена равен нулю.

Доказательство. Рассмотрим ряд 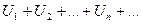. Так как 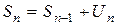, то 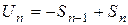. Так как по условию ряд сходится, то обе частичные суммы стремятся к S, то есть 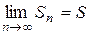и 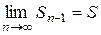, значит .

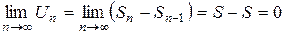Замечание. Обратное утверждение к теореме, вообще говоря неверно, то есть из того, что 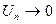ещё не следует, что ряд сходится.

С помощью теоремы можно доказать только расходимость ряда, то есть если 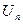не стремится к нулю, то ряд расходится. Если же 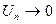, то о сходимости или расходимости ряда вывода сделать нельзя, надо проводить дополнительное исследование.

Пример. 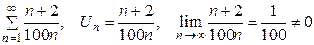– ряд расходится.

Дата добавления: 2014-01-07