Отличительные признаки и показатели

Здесь

β = P_d[рад]/ T_J[c]; ω_o² = E_qoU2πf/ T_J[c] x_d∑ [1/c²]

F (t}— внешняя сила; f—50 Гц—частота сети.

Если рассматривать большие колебания угла δ роторасинхронной машины относительно вектора напряжения системы и искать приближенное (гармоническая линеаризация) периодическое решение в виде ряда Фурье:

δ = a_o+ a₁ sin (ωt + φ₁),

где a_o — постоянная составляющая; a₁ —амплитуда первой гармоники, тонелиней­ная функция в комплексной форме запишется как

sinδ = sin[a_o+a₁ sin (ωt + φ₁)] = ∑S_ne^jωnt = S_o +(S_—1 + S₁)e^jωt.

Здесь S_n—коэффициенты разложения в ряд Фурье:

S_o = J_o(a_o) sin a_o; S₁ = [2J₁ (a₁/a]ξ₁ cos a_o;

S_—1 [2J₁ (a₁)/a₁]ξ_—1cos a_o.

При этом J_o(a₁) и J₁(a₁) -- функции Бесселя первого рода; ξ₁ и ξ_--1— компексно - сопряженные

амплитуды колебания угла δ, связанные с действительной

амплитудой следующим соотношением:

ξ₁e^jωt + ξ_—1e^—jωt = a₁ sin(ωt + (a₁/2j)[e^{j(ωt + φ1)} e^{—j(ωt +φ1)}], откуда

ξ₁ = (a₁/2j) e^jφ1; ξ_—1 = --(a₁/2j) e^—jφ1.

Рассмотрим свободные колебания, когда в правой части (5-24 ) стоит момент турбины, определяющий установившееся значение угла δ = δ_o, т.е F(t) = ω_o² sin δ_0. Приравнивая коэффициенты при одинаковых гармониках, получим уравнении n = 0 и n =1) для постоянных составляющих и первых гармоник соответственно:

J_o(a₁) sin a_o = sinδo; (3--25)

(--ω² + jβω)ξ₁ + ω² [2J(a₁)/a₁]ξ₁ cos a_o = 0. (3—26)

(7-26)

Уравнение (3-25) определяет связь между средней точкой и амплитудой ко­лебания угла:

sin a_o = sinδ_o/[ J_o (a₁)] (3-27.)

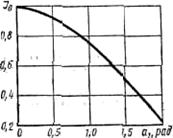
Функция Бесселя J_o(a₁₎ уменьшается с увеличением a₁ (рис. 3-10), начинаясь при a — -0 от J_o (a₁). Уравнение (3-27) показывает, что при малых a₁ система

Рис. 3-10 Рис. 3.11

РАЗДЕЛ 4

МАТЕМАТИЧЕСКИЙ АППАРАТ ДЛЯ ИЗУЧЕНИЯ СТАТИЧЕСКОЙ УСТОЙЧИВОСТИ УСТАНОВИВШЕГОСЯ РЕЖИМА

4-1. ЗАДАЧИ ИССЛЕДОВАНИЯ

При разработке устройств и систем инженеру приходится при­нимать во внимание, что параметры систем, внешние условия, в которых они вынуждены работать, не бывают постоянными, не­изменными во времени Изменение их во времени приводит к воз­никновению в эксплуатируемых устройствах и системах переходных процессов- Поэтому для оценки работоспособности системы и уста­новления качества работы ее в реальных условиях инженеру необ­ходимо изучать свойства переходных процессов, разрабатывать спе­циальные мероприятия и устройства, обеспечивающие нужные свой­ства переходных процессов.

На первом этапе создания или развития всякий технической системы определяется ее работоспособность, т. е. устойчивость состоя­ния равновесия при малых от него отклонениях. Способность си­стемы возвращаться в исходное или близкое к исходному положению после малого возмущения (начального отклонения параметров) назы­вается устойчивостью состояния равновесия или статической устойчивостью.

Широкий класс технических устройств, к которому относятся и автоматически регулируемые электрические системы, при изучении переходных процессов после малых возмущений может быть описан системами обыкновенных дифференциальных уравнений с постоян­ными коэффициентами:

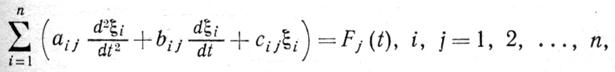
(4-1)

где a_ij, b_i, c_ij -- постоянные коэффициенты, зависящие от пара­метров системы; ξ₁, ξ₂,..., ξ_n -- переменные, характеризующие состояние системы в каждый момент времени; F₁ (t), ..., F_n (t)— внешние силы, переменные по времени, отражающие изменение внешних условий работы системы.

Предположение о линейности рассматриваемой системыдиффе­ренциальных уравнений заставляет учитывать еще ряд обстоятельств при изучении переходных процессов. Как правило, дифференциальные уравнения, описывающие переходные процессы в технических устройствах нелинейны вследствие нелинейности физических законо­мерностей, зависимости параметров системы от переменных ξ_i и т. п. Однако изучение нелинейных систем представляет собой весьма трудную задачу, не имеющую универсальных методов решения. Поэтому нелинейную систему уравнений стремятся свести к хорошо изученной линейной системе с постоянными коэффициентами. Это возможно при следующих условиях:

1) возмущающие силы F j (t)незначительно меняются во времени,

т. е.

(4-2)

При F_j(t) = F_j0 система (3-1) имеет решение

т.е. 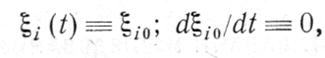(4-3)

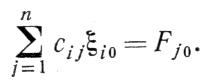(4-4)

Это решение соответствует состоянию равновесия (иногда физически это может соответствовать состоянию установившегося дви­жения). Относительно же функций f_j(t) предполагается, что они малы по величине;

2) рассматриваются лишь такие изменения ξ_i (t), ξ_i^ (t) и ξ_i^(t),

при которых величины малы. При

необходимости приходится сокращать промежуток времени, на ко­тором система рассматривается как линейная. Такая ситуация воз­никает, когда решение линейной системы таково, что 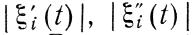возрастают во времени неограниченно. Вводя указанные предположения» т. е. считая малыми

f_j(t) = | F_j(t) – F_j0 |, |ξ_i ^*(t) |, |ξ ^**_i(t)|,

нелинейные функции, входящие в дифференциальные уравнения, линеаризуют в точке, соответствующей F_j(t) ≡F_j0, ξ _j≡ ξ _j0, ξ_j^*=0, ξ_i^** = 0, и тем самым получают линейные уравнения с постоянными коэффициентами.

Коэффициенты же а _ij, в_ij, с_ij оказываются зависимыми от точки равновесия ξ_i0, F_i0 . Таким образом, изучение влияния внешних условий на поведение системы сводится к изучению пове­дения решении системы (3-1) при различных

f_j (t), где коэффициенты а, b,c также зависят от внешних сил F_j0.Введем замену переменных:

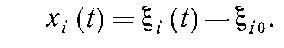(4-5)

Очевидно, что

Тогда система (4-1) преобразуется:

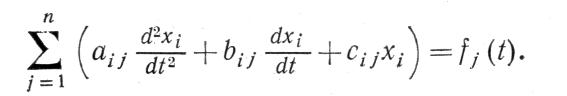(4-6)

Состоянию равновесия (4-3) системы (4-1) соответствует, оче­видно, состояние равновесия системы (4-6);

x_i=0 (4-7)

при

f _j(t)=0. (4-8)

причем x _i(t) можно понимать как отклонение от состояния равно­весия, fj (t) – как возмущающие силы.

Рассмотрим систему (4-6). Условиям 1) и 2), указанным выше для этой системы, согласно замене (4-5) будут соответствовать предположения, что величины малы.

Выявление свойств переходных процессов на основе изучения системы (4-6) сводится к следующему. Каждому набору функций и набору начальных условий

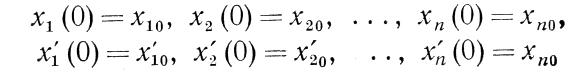
будет соответствовать решение системы (4-6);

Это решение и будет представлять собой переходный процесс во

времени.

Возможны два решения поставленной задачи:

1) получение x₁(t), x₂(t), …. При заданных начальных условиях и f₁(t),…..,f_n(t) в «замкнутой форме» (в виде аналити­ческих формул) или в виде некоторого набора значений этих функ­ций через равноотстоящие промежутки времени;

2) получение суждения о свойствах процесса без получения са­мих решений.

Второй подход, весьма удобный и наименее трудоемкий, и будет рассматриваться далее как соответствующий задаче выяснения ра­ботоспособности технической системы, т, е. определения устойчи­вости состояния равновесия. Первый путь решения используется для оценок качества переходных процессов.

3-2. УСТОЙЧИВОСТЬ СОСТОЯНИЯ РАВНОВЕСИЯ

При математической оценке устойчивости, определенной как спо­собность системы возвращаться в исходное или близкое к исходному положению после малого возмущения, необходимо иметь в виду

следующее строгое положение. На промежутке t(-- ∞, t₀) (в ка­честве t₀ часто берут t=0) возмущающие силы f_j(t) вызывают отклонения системы от состояния равновесия:

В момент времени t = t₀ действие возмущающих сил прекращается [f_j (t)= 0 (t > t₀) и далее имеет место переходный процесс, обу­словленный, как говорят, начальными возмущениями. Переходный процесс при этом соответствует решению системы уравнений

с начальными условиями, приобретенными при действии возмущающих сил до t< t₀. '

Положение равновесия системы (4-9) называется устойчивым по Ляпунову, если для любого ε > 0 можно найти такое δ > 0, что все решения системы с начальными условиями |x_i0|<δ, |x_i0^* | <δ для t>t₀ будут удовлетворять |x_i(t) < ε.

Положение равновесия называется асимптотически устойчивым, если оно устойчиво, и решения, кроме того, удовлетворяют условию

1im x_{i (t)}=0, при t→0, (4-10)

т. е. возмущенное движение асимптотически приближается к со­стоянию равновесия. ^!

Свойство, обратное устойчивости, называется неустойчивостью.

Очевидно, что устойчивость состояния равновесия является не­обходимым условием работоспособности системы. В противном случае малые начальные отклонения, которые всегда имеют место в реаль­ных условиях, будут вызывать нарастающие со временем отклоне­ния и, как следствие, недопустимое изменение условий работы системы.

Согласно приведенному определению устойчивости изучаются общие свойства решений однородной системы (4-9), способность их группироваться вблизи состояния равновесия, а не расходиться от него со временем. Эта способность связана с возникновением внут­ренних сил системы, противодействующих ее удалению от состояния равновесия. При дальнейшем развитии теории устойчивости (после Ляпунова) было показано, что если состояние равновесия системы (3-9) асимптотически устойчиво, то и при действии возмущающих сил, произвольных но виду, но малых но величине, от­клонения переменных x_i(t) также будут малы, т. е. будет иметь место устойчивость системы и при длительно действующих возмущениях. Это положение известно в теории устойчивости как тео­рема И. Г. Малкина.

Если состояние равновесия системы (3-9) асимптотически устой­чиво, то для любого ε можно найти такие δ>0 и ξ>0, при начальных отклонениях

|x_i0 | < δ, | x_i-^*| < δ (4-11)

и любых возмущающих силах f_i (t), удовлетворяющих условию

|f_j(t) < ξ, (4-12)

решения системы (4-6) для всех t > t₀ удовлетворяют условию

| x_i (t) < ε. (4-13)

Рассмотрим решение системы исходных уравнений (3-1) в опера­торной форме при начальных условиях, отражающих появление отклонений и производных в момент t =t₀ (F_j = Y_j)

/=1

Р/^Р^^Р) 0(р)

Начальные условия: При этом X_i (p) имеет полюсы, совпадающие с корнями главного определителя D (р), т. е. с корнями р_1, р₂,..., р_n, - урав­нения

. (4-14)

(Полюсами X_i(p) называются нули знаменателя, т.е. такие значения комплексного переменного р, при котором значения X_i(p) обращаются в бесконечность.)

Уравнение (4-14) называется характеристическим (п— степень характеристического уравнения). Других полюсов X_i (р) не имеет, так как функция D_ji(p) Yj (p) в этом случае является целой. Пола­гая корни уравнения (3-14) простыми и используя теорему разло­жения, получаем оригинал

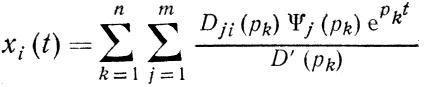(3.15)

[аналогично можно получить и оригинал для Х_i(p) при учете f_j (t),

однако в этом случае полюсы X_i (р) содержат не только корни характеристического многочлена, но и полюсы F_j (p)].

Из выражения (3-15) видно, что поведение системы во времени определяется корнями характеристического уравнения. В самом деле, если корни уравнения (3-14) все простые и имеют отрица­тельные вещественные части, то решение (3-15) можно сделать сколь угодно малым для всех t > 0 выбором достаточно малых верхних пределов начальных условий, так как каждое из слагаемых выра­жения (3-15) линейно и однородно зависит от х_i0, x_i0^* и имеет со­множитель е ^{- akt}, где показатель а _k> 0—экспоненциально убыва­ющий во времени.

В случае кратных корней в аналитическое выражение (3-15) будут входить, кроме экспонент вида е-^akt, некоторые полиномы от t. Это, однако, не изменит устойчивости состояния равновесия, так как при а _k > О,

.

что легко проверить, применив п раз известное правило Лопиталя.

Поэтому и в общем случае можно сказать, что положение равновесия системы (4-6) будет асимптотически устойчиво тогда и только тогда, когда все корни характеристического уравнения (4-14) имеют отрицательные вещественные части; положение равновесия будет неустойчивые, если хотя бы один корень уравнения (4-14) имеет положительную вещественную часть.

Если среди корней уравнения (4-14) имеются корни с нулевыми вещественными частями, то в случае, когда корни простые, поло­жение равновесия системы (3-6) устойчиво, но не асимптотически. Если же эти корни кратные, то может иметь место как устойчи­вость, так и неустойчивость.

Вопрос о том, насколько правомерно переносить суждение об устойчивости состояния равновесия упрощенной линеаризованной системы на исследуемую систему, описываемую нелинейными урав­нениями, был подробно исследован основоположником теории устой­чивости акад. А. М. Ляпуновым. На основании результатов, полу­ченных им, сделан вывод: если состояние равновесия линеаризован­ной системы асимптотически устойчиво, то состояние равновесия нелинейной системы также асимптотически устойчиво; если состоя­ние равновесия линеаризованной системы неустойчиво, то неустой­чиво и. состояние равновесия нелинейной системы.

В случае, если среди корней характеристического уравнения линеаризованной системы имеются корни с нулевой действительной частью, то для ответа на вопрос об устойчивости нелинейной си­стемы недостаточно проанализировать линеаризованную систему:

надо учитывать нелинейные функции. Наличие корней характе­ристического уравнения с нулевыми действительными частями (ос­тальные корни имеют отрицательные вещественные части) свиде­тельствует о границе устойчивости. При этом малые изменения параметров системы могут приводить как к устойчивости, так и к неустойчивости.

3-3. НЕОБХОДИМЫЕ И ДОСТАТОЧНЫЕ УСЛОВИЯ УСТОЙЧИВОСТИ

Условие устойчивости называется необходимым, если при невы­полнении его появляется неустойчивость; условие устойчивости называется достаточным, если при его выполнении имеет место устойчивость; условие устойчивости необходимое, но недостаточное, означает, что его выполнении недостаточно для того, чтобы имела

место устойчивость: может появиться как устойчивость, так и неустойчивость. Вопрос об устойчивости должен в этом случае решаться дополнительными исследованиями. Необходимое и достаточное условие статической устойчивости обеспечивается тогда и только тогда, когда все корни характеристического уравнения этой системы

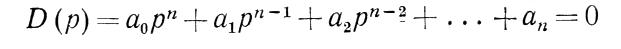(4-16)

имеют отрицательнее вещественные части.

•Так как коэффициенты уравнения (4-16), определяемые реальными параметрами технической системы, всегда действительны, то его корни могут быть действительными и комплексно-сопряженными.

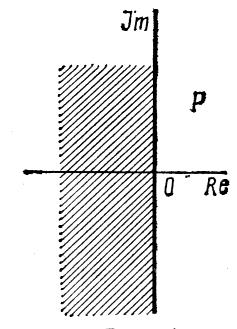
Рис. 3-1

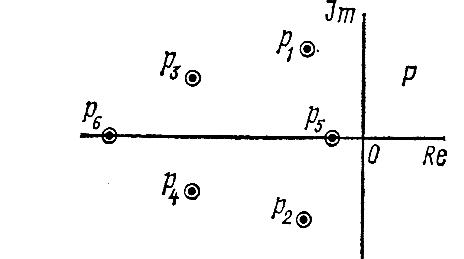
Рис 4-2

Рассматривая корни характеристического уравнения как точки

комплексной плоскости (рис. 4-1)

(4-17)

приведенное условие можно сформулировать и так: для того чтобы состояние равновесия было асимптотически устойчиво, необ­ходимо и достаточно, чтобы все корни р₁, р₂,...,р_n характери­стического уравнения (4-14) лежали в левой полуплоскости корней (или, кратко говоря, были бы левыми) (рис. 4-2).

Характеристическое уравнение электрической системы обычно содержит несколько действительных корней и несколько комплексно-сопряженных.

При простых корнях характеристического уравнения [в (3-17) нет одинаковых корней] общее решение системы (3-9)

(4-18)

где С_ik—постоянные, зависящие от начальных условий.

|

При этом действительному корню p_i = α_i(ω = 0) соответствует

в решении член С _ik е^αit, где С_ik—действительное число.

Паре комплексно-сопряженных корней соответствуют два члена в решении 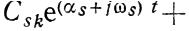и всегда (при любых начальных | условиях) комплексно-сопряженные:

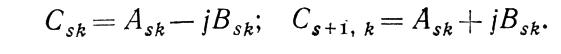
Исходя из последних уравнений, можно запис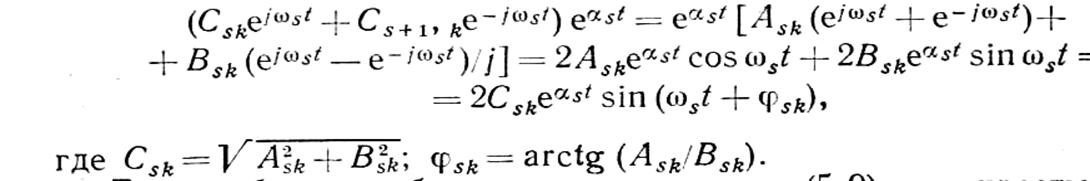(4-19)

Таким образом, общее решение системы (3-9) при простых кор­нях характеристического уравнения состоит из членов вида

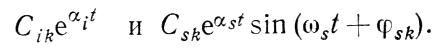
Следовательно, значение корней характеристического уравнения указывает не только на устойчивость либо неустойчивость, но и

Рис. 4-4 Рис. 4-3

позволяет установить вид функций, составляющих переходный

процесс.

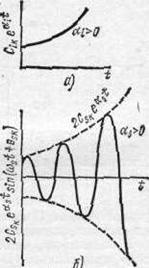
Если все α_i, α_s отрицательны, т. е. корни лежат в левой полу­плоскости, то все составляющие по модулю экспоненциально зату­хают [у составляющих вида (4-19) экспоненциально затухает ампли­туда колебаний (рис. 4-3, а, б)].

Если среди действительных корней имеется хотя бы один с α_i > 0, то составляющая решения, соответствующая этому корню, по модулю неограниченно возрастает во времени (рис. 4-4, а). Система оказывается неустойчивой. При этом говорят, что проис­ходит апериодическое нарушение устойчивости.

Если же среди комплексных корней имеется хотя бы одна пара с α_i > 0 (опийные корни левые), то соответствующая этой паре корней составляющая решения имеет вид экспоненциально нарастающих

во времени колебаний (рис. 4-4, б). Система неустойчива, при этом говорят, что происходит колебательное нарушение устойчивости, или с а м о р ас к а ч и в а н и е.

Если система оказывается неустойчивой, инженеру важно еще знать, как происходит нарушение устойчивости. Зная характер нарушения устойчивости, иногда из чисто физических соображений можно наметить мероприятия, устраняющие нарушение устойчивости. Поэтому в процессе решения задачи устойчивости желательно полу­чить представление и о характере нарушения устойчивости.

Выявление возможной неустойчивости и определение хода про­цессов при нарушении может быть проведено путем отыскания корней характеристического уравнения (4-14). Однако при высокой степени уравнения задача отыскания его корней оказывается весьма трудоемкой. Поэтому при исследовании устойчивости часто исполь­зуют закономерности, связывающие положение корней уравнении (4-14) в левой полуплоскости со знаками коэффициентов а _0, ......., а _n и некоторых функций от этих коэффициентов, а также закономер­ности, связывающие частотные характеристики системы с устойчи­востью или неустойчивостью и т. п. Далее излагается ряд наиболее распространенных критериев и методов изучения устойчивости. Одновременно указываются способы установления характера нару­шения устойчивости.

4-4. АЛГЕБРАИЧЕСКИЕ КРИТЕРИИ УСТОЙЧИВОСТИ

Общая характеристика критериев. Алгебраические критерии устойчивости основаны на закономерностях, связывающих отрица­тельность всех действительных частей корней уравнения (4-14) со знаками коэффициентов этого уравнения и некоторых функций от коэффициентов. Алгебраические критерии содержат группу усло­вий (группу неравенств), при соблюдении которых имеет место устойчивость; если же хотя бы одно из них нарушено, то имеет место неустойчивость. Для проведения анализа устойчивости с помощью алгебраических критериев необходимо предварительно вычислить коэффициенты характеристического уравнения

.

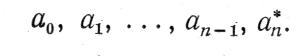
Необходимые условия устойчивости. При использовании алгеб­раических критериев устойчивости полезно иметь в виду следующее необходимое условие устойчивости: если состояние равновесия системы (4-9) асимптотически устойчиво, то все коэффициенты положительны:

Докажем это. Разложим характеристический многочлен на мно­жители:

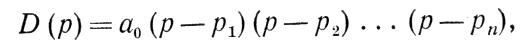(4-20}

где p₁,…..,p_n корни характеристического уравнения.

Если объединить попарно множители, соответствующие комплексно-сопряженным корням, τυ правую часть (4-20) можно представить в виде произведения линейных и квадратичных множителей. Если а < 0, то множители, соответствующие парам комплексно-сопряжен­ных корней, дают квадратичные полиномы вида

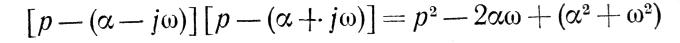(4-21) f

и имеют все положительные коэффициенты. Линейные множители (р—а_i) при а_i < 0 также положительны. Следовательно, характе­ристический многочлен, полученный как произведение многочленов с положительными коэффициентами, имеет также положительные коэффициенты. Если это необходимое условие устойчивости не выполнено, то система заведомо неустойчива. Однако обратное утверждение неверно. Система может быть неустойчива, несмотря на то что все коэффициенты характеристического уравнения поло­жительны.

Характеристическое уравнение с положительными коэффициен­тами обладает важным свойством—оно не имеет действительных положительных корней. Действительно, каждый корень должен превращать многочлен (3-20) в нуль. Если корень действительный и положительный, то он не может превратить в нуль уравнение с положительными коэффициентами.

Таким образом, положительность всех коэффициентов характе­ристического уравнения есть необходимое и достаточное условие отсутствия апериодической неустойчивости. Из него следует, что если при изменении параметров система ста­новится неустойчивой, а коэффициенты характеристического урав­нения при этом положительны, то нарушение устойчивости имеет характер самораскачивания.

Если при изменении параметров устойчивой системы становится отрицательным свободный член характеристического уравнений то нарушение устойчивости носит апериодический характер. Πоκажем это. Положив в (4-20) р=0, получим свободный член характеристического многочлена

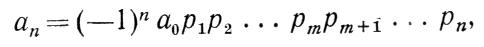(4-22)

который равен произведению всех корней на (—Ι)ⁿ a₀ . Здесь m— число действительных корней, (n—m)—число комплексно-сопря­женных корней. Очевидно, (n — m) четно, поэтому (—1)ⁿ=(—1) ^m и _n ={—\)'ⁿa⁰ p₁...p_n.

Произведение двух комплексно-сопряженных корней положи­тельно при любых α и ω:

(α + jω) (α — j w) = α² + ω²,

поэтому (p_m+1 p_m+2 ….p_n > 0 - При p_i= -- α_i, где а_i > 0, все действительные корни лежат в левой полуплоскости. При перемно­жении всех действительных корней справедливо соотношение

Свободный член характеристического уравнения всегда при этом

положителен:

. (4.23)

.

Если при изменении параметров системы только один действительный корень перейдет из левой полуплоскости в правую, то а_n изменит знак, т.е. станет отрицательным.

Необходимые и достаточные условия устойчивости. Для устойчивости системы требуется, чтобы коэффициенты характеристического многочлена не только были положительными, но и удовлетворяли некоторым соотношениям.

К р и те ρ и й Г у ρ в и ц а устанавливает эти соотношения в форме неравенств, соблюдение которых является необходимым и достаточ­ным условием устойчивости системы любого порядка.

Система неравенств Гурвица строится следующим образом. Из коэффициентов характеристического многочлена n-й степени

составляется матрица Гурвица квадратная,n-го порядка:

(4-25)

Правило составления (алгоритм) матрицы Гурвица следующее. По главной диагонали располагают коэффициенты многочлена (3-24) в порядке их нумерации, начиная с а ₁ до а_n. В строках помещают поочередно коэффициенты только с нечетными или только с чет­ными индексами (включая и коэффициент а₀), причем влево от диагонали с уменьшающимися, вправо—с увеличивающимися ин­дексами. Все недостающие коэффициенты, т. е. коэффициенты с ин­дексами меньше нуля или больше n, заменяют нулями. Для соблю­дения устойчивости требуется, чтобы все n диагональных минора матрицы (3-25) были положительными. Диагональные миноры (назы­ваемые определителями Гурвица) получаются отчеркиванием их слева и сверху, как показано в матрице (3-25). Таким образом, критерий устойчивости Гурвица записывается как

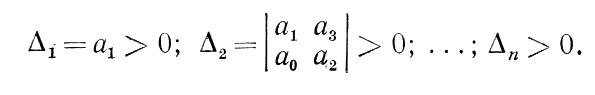(4-26)

Заметим, что последний определитель Δ_n включает в себя уже всю матрицу Гурвица целиком. Если его раскрыть по элементам последнего столбца, содержащего только коэффициент а_n (свободный член характеристического уравнения), то можно записать Δ_n = a_n Δ_n-1.

Гурвиц показал, что если непрерывно изменять коэффициенты характеристического уравнения, ухудшая устойчивость системы, то при потере устойчивости прежде всего обратится в нуль опре­делитель Δ_n. Если при этом Δ_n-1 > О, то граница устойчивости определяется условием a_n=0. Это граница апериодической устой­чивости (один действительный корень находится на мнимой оси плоскости корней). Если а_n > 0, то в нуль обращается Λ_n-1, что соответствует наличию на границе пары чисто мнимых корней р _1,2 =jω. Это граница колебательной устойчивости. При пере­ходе через эту границу начинается самораскачивание системы с частотой ω₁. Если и дальше изменять коэффициенты, то могут стать отрицательными и другие определители Гурвица, а Λ_n-1_ι вновь.может стать положительным. Поэтому положительность а_n и Δ_n-1 (а значит и Δ_n) еще не свидетельствует об устойчивости: должны быть положительными также и остальные определители Гурвица.

Для определения числа корней в правой полуплоскости удобно использовать следующее положение. Если в ряду (a₀, Δ₁, Δ₂/’Δ₁,......, δ _n-1/δ_n-2, Δ _n/Δ _n-1) некоторые элементы последовательности отрицательны, то число перемен знака в этой последовательности равно числу корней в правой полуплоскости. Так как последний элемент последовательности Δ_n/Λ_n-1==α_n, то перемена знака а_n с положительного на отрицательный при всех остальных положи­тельных определителях Гурвица соответствует одной перемене знака в ряду, а следовательно, определяет наличие одного (действитель­ного) корня в правой полуплоскости. Если же δ _n-1 меняет знак с положительного на отрицательный, а все остальные определители Гурвица и свободный член a_n положительны, то это соответствует двум переменам знака в ряду и определяет наличие двух (при положительности всех коэффициентов многочлена) комплексно-сопряженных корней.

В качестве примера приведем условия устойчивости Гурвица для характеристического уравнения третьего порядка. Определитель Гурвица имеет вид

Условиями устойчивости являются

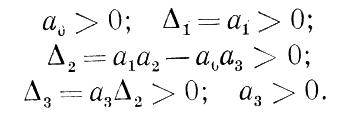
. Из условия Δ₂ > 0 следует, что а₂ > 0. Следовательно, кроме положительности всех коэффициентов характеристического уравнения, коэффициенты должны удовлетворять соотношению а₁а₂ -- а₀а₃ > 0. Нарушение этого соотношения приведет к самораскачиванию системы.

Критерий Рауса более удобен для систем высокого порядка с численно заданными параметрами и, следовательно, коэффици­ентами характеристического уравнения.

Из коэффициентов характеристического многочлена

составим таблицу Рауса (табл. 3-1) с числом строк (n+1)· Укажем правило составления (алгоритм) таблицы Рауса и ее коэффициен­тов. Элементами первой строки являются все коэффициенты с чет­ными индексами, а элементами второй строки—с нечетными индек­сами. Элементы каждой следующей строки найдем по формуле

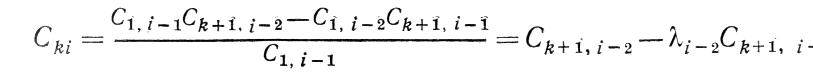
где k—номер столбца; i—номер строки, в которой находится коэф­фициент

Требования устойчивости по Раусу формулируются так: для устойчивости системы необходимо и достаточно, чтобы все коэффи­циенты первого столбца были положительны:

(4-27)

Число перемен знака в первом столбце таблицы Рауса указы­вает на число корней характеристического уравнения D (р) = О, расположенных в правой полуплоскости. Таким образом, если тре­буется рассчитать только устойчивость, то составление таблицы Рауса прекращается, как только элемент первого столбца какой-либо строки станет отрицательным. Если требуется определить число корней в правой полуплоскости, то таблица Рауса составляется полностью,

Приведенное правило составления таблицы Рауса применяется в том случае, если в первом столбце не встречаются числа, равные нулю.

3-5. КРИТЕРИЙ УСТОЙЧИВОСТИ МИХАЙЛОВА

Критерий Михайлова является частотным критерием устойчи­вости. В его основу положен принцип аргумента, известный из теории функций комплексного переменного. Критерий устойчивости формулируется следующим образом. Для отсутствия.корней характеристичеcкого уравнения с положительной действительной частью,

Рис. 4-5 Рис. 4-6

т. е. обеспечения устойчивости системы, необходимо и достаточно, чтобы при прохождении точкой p мнимой оси в положительном направлении приращение аргумента D (p) было равно nπ.

Проиллюстрируем правило Михайлова, для чего представим характеристический многочлен (a₀ > 0) в виде произведения простей­ших множителей;

D (p) = a₀ (p – p₁) (p – p_{2) ……………}(p – p_n),(3-28)

где a₀—коэффициент при рⁿ — корни характеристи­ческого уравнения D(p)=-0.

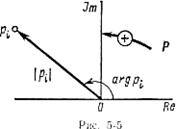
Каждому корню на комплексной плоскости ρ соответствует точка. Геометрически корень p_i I может быть представлен вектором, соеди­няющим начало координат с точкой р_i (рис. 4-5). Множитель (ρ—ρ_i) представляет собой на плоскости Р разность векторов; р, направ­ленного произвольно, и p_i (рис. 4-6).

Направим вектор р по мнимой оси Jm, т.е. положим p==jω. Тогда конец вектора jω—ρ _iбудет лежать на мнимой оси. При изменении ω конец вектора будет скользить по оси Jm, поворачи­ваясь в направлении, зависящем от расположения корня р_i на плоскости корней.

Рассмотрим корень р_i; лежащий в левой полуплоскости, т. е. а_i < 0 (рис. 4-7). Вектор jω—рi при изменении ω от —∞ до +оо перемещается в положительном направлении, т. е. против часовой стрелки. При этом аргумент вектора jω—р_i получает приращение + π.

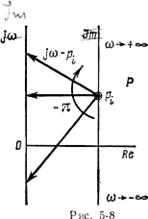
Рассмотрим корень p_i лежащий в правой полуплоскости (рис. 4-8), когда а_i > 0. Вектор jω—ρ_i- вращается при изменении ω от —σο до по часовой стрелке, т. е.

Δ arg(jω— p_i) =—π.

Многочлен D (p) при подстановке p = jω представляет собой век-

тορ, который называется характеристическим:

D (jω) =a₀ (jω – p₁)j/ω – p₂)...(j·ω -p_n). 4-29)

Модуль D (/ω) равен произведению модулей единичных векторов, фаза или аргумент—сумме аргументов единичных векторов;

argD (/ω) = arg (/ω— p₁) + arg (/ω— p₂)+· · · + arg(jω— p_n). (4-30) Если все корни p_1, p₂..., р_n лежат в левой полуплоскости, то ΔargD(jω)=

Если среди n корней характеристического уравнения m корней

лежат в правой полуплоскости, а (n— т) корней—в левой полу-

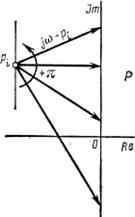
Рис. 4-7

плоскости, то при изменении ω от --∞ до + ∞ приращение аргумента

Δ arg D (/ω) = (n — m) π –mπ = (n – 2m)π (4-32)

- Рис..4-8

Таким образом, правило аргумента гласит: приращение аргумен­та вектора D (jω) при изменении ω от — оо до + oo равно раз­ности между числом (n—m) корней характеристического уравнения D{ρ} = 0, расположенных в левой полуплоскости, и числом m корней, лежащих а правой полуплоскости, помноженной на π.

Для устойчивой системы необходимо, чтобы вы­полнялось условие (4-31). При практическом использовании этого правила обычно разделяют действительную и мнимую части вектора D(jω):

D(jω) = U (ω) + j V (ω). (4-33)

Вектор D (jω)изображенный в декартовых координатах на плос­кости D(jω), при изменении ω от —∞ до + ∞ вращается и концом описывает кривую (рис. 3-9), которая называется характеристичес­кой кривой или годографом характеристического уравнения.! Многочлен

U(ω) = a_n + a_n-2(jω)² + a_n-4 (jω)⁴ + ….a_n – a_n-2 ω² + a_n—4 ω⁴ -- …

является четным относительно ω, τ. е.U (ω)==U(—ω). Многочлен

является, нечетным относительно ω, т. е. V(ω)= --V (— ω), откуда следует, что годограф симметричен относительно действительной оси (рис. 4-10). Учитывая это, запишем критерий Михайлова в следующей формулировке: система будет устойчива тогда и только тогда, когда при возрастании ω от 0 до оо вектор D(jω) повернется на угол 0,5πn, где п—степень характеристического уравнения, или,,

Зт

Рис. 4-9 Рис. 4-10

что то же самое, если при увеличении ω от 0 до +оо годограф, начинаясь на положительной части действительной оси, проходит последовательно в положительном направлении n квадрантов:

Δ агgD (jω) = 0,5πn. (4-34)

0< ω < ∞

Если система неустойчива и т корней расположено в правой полуплоскости, то

Δ агg D (jω) = 0,5π (п—2т). (4-35)

0< ω< ∞

Это условие дает возможность по кривой Михайлова судить не только об устойчивости системы, но и о числе корней в правой полуплоскости неустойчивой системы.

В устойчивой системе длина характеристического вектора при всех значениях ω должна быть отлична от нуля, причем вектор с изменением ω от 0 до оо должен поворачиваться монотонно, из

чего следует, что:

Ι) D(0) > О—начало годографа лежит на положительной части действительной оси;

2) V*(0) > 0—в начале годографа положительному приращению Δω соответствует положительное приращение ΔV(ω);

3} годограф D(jω) поочередно пересекает оси U =0 и V==0, т. е. нули уравнений U (ω) == 0 и V (ω) = 0 — действительные и переме­жающиеся. ·, -

Так как первое пересечение оси Υ(ω)=0 происходит при ω=0, arg D (jω) = 0,5πn, то число пересечений равно степени n харак­теристического уравнения. Этот вы­вод позволяет сформулировать кри­терий устойчивости в другом, более удобном виде.

Для обеспечения устойчивости необходимо и достаточно вы­полнение следующих условий (рис. 3-11):

1) U(0)=a_n>0;

2) V*(0) =а _n-1>0, где V*(ω)= dV/dω;

3) все корни уравнений U(ω)==0 иV(0)-=0 действительные и переме­жающиеся, т. е. между любыми дву­мя соседними корнями уравнения V (ω) = 0 лежит один корень уравнения U (ω) = 0 (рис. 3-12).

Рис. 4-11:

Существование комплексных корней уравнений U (ω) ·= 0 или V(ω) = 0 либо отсутствие перемежаемости корней этих уравнений свидетельствует о неустойчивости системы. Поскольку для анализа устойчивости достаточно рас­смотреть свойства годографа при О < ω < ∞, то следует ограни-

Рис. 3-12 Рис. 4-13

читься определением неотрицательных корней уравнений U(ω) = 0 или V(ω) = 0.

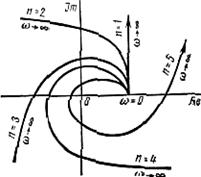
Типичные годографы устойчивых систем D (jω) для характерис­тических уравнений различных степеней n от 1 до 5 приведены на

рис. 4-13. Характеристическая кривая устойчивой системы при из­менении ω от 0 до ∞ должна охватывать начало координат.

На рис. 4-14 и 4-15 показаны примеры годографов неустой­чивой системы.

При построении кривой Михайлова обычно задаются дискретным рядом значений ω от 0 до некоторого значения ω_max, которое выби-

Рис. 4-14

Рис.4-15

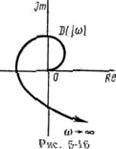
раетcя различным для каждого случая и зависит от порядка харак­теристического уравнения и коэффициентов. Однако в критерий Ми­хайлова входит величина приращения аргумента вектора D (jω), получающаяся при изменении ω от 0 до + ∞. Поэтому необходимо исследовать поведение вектора при ω → ∞. Это можно сделать в об­щем виде, не задаваясь конкретными значениями коэффициентов. Рассмотрим lim [D(jω)/ a₀ (jω)ⁿ] при ω→ ∞:

так как все остальные члены при ω→∞ стремятся к нулю. Сле­довательно, и агg (jω)) при ω —> оо будет стремиться к агg (jω)ⁿ Так как характеристический многочлен всегда приводится к та·

Рис. 4-17

кому виду, что а₀ > 0, то независимо от того, устойчива или неус­тойчива система, характеристическая кривая D (jω) при а₀ > 0 и ω—оо выходит в n-й квадрант. Наклон кривой Михайлова в n-м квадранте при ω —> оо определяется двумя первыми членами D (jω): а₀ (jω)ⁿ + (jω)^n-1 .

Дата добавления: 2014-01-07