Марковские процессы

КЛАССИЧЕСКИЕ КООПЕРАТИВНЫЕ ИГРЫ

Как правило, в конфликтных ситуациях участвуют не два, а значительно большее число участников.

Введем следующие обозначения:

I – множество всех игроков;

S – коалиция игроков, которая выступает как единый игрок.

Определение 1. Кооперативной игрой n лиц называется пара (I, V), где I ={1, 2, 3, ×××, n }, а V –вещественная функция, определенная на всех подмножествах S Ì I, где V (Æ).

Обозначения:

n – количество игроков, участвующих конфликте и объединившихся в коалицию I;

S – коалиция игроков, выступающая как единый игрок (S Ì I);

V – характеристическая функция игры, область определения которой состоит из 2n возможных подмножеств I;

V (Æ)=0 означает, что значение характеристической функции от пустого множества равна нулю.

Пример: n =3, т.е. коалиция I включает в себя всех трех игроков, тогда возможные коалиции S:

– одноэлементные коалиции, состоящие из одного игрока: S {1}, S {2}, S {3};

– двухэлементные коалиции: S {1, 2}, S {1, 3}, S {2, 3};

– трехэлементные коалиции: S {1, 2, 3}.

V (S)– характеристическая функция, которая определяет гарантированный выигрыш каждой из возможных коалиций S, которые могут образовывать участники конфликта.

V (S {1})– гарантированный выигрыш коалиции S, который состоит из первого игрока (точно также 2-го и 3-го, и также вместе 1,2; 1,3 и 2,3); этот выигрыш первый игрок может обеспечить себе даже в худшем для себя варианте, а именно: даже в том случае, если он действует самостоятельно, ни с кем не кооперируясь, а остальные два игрока образуют коалицию, которая выступая как единый игрок, будет действовать против него;

V (1)– гарантированный выигрыш самой большой коалиции I, которая объединила всех трех игроков.

Количество возможных подмножеств множества I, на которых определена характеристическая функция V (S), в рассматриваемом нами примере равно: 2 ⁿ =2³=8. Это число получается, как сумма: 3-х одноэлементных коалиций, 3-х двухэлементных коалиций, одна трехэлементная и пустого множества, при котором V (Æ)=0.

Перед решением таких задач, необходимо проанализировать вариант – а выгодно ли объединяться с точки зрения увеличения выигрыша, формально это выглядит так: где S Ì I, В Ì I и S Ì I Ç В =Æ, где S и В не пересекающиеся коалиции. Если неравенство выполняется, то характеристическая функция игры называется супераддитивной.

Супераддитивность указывает на то, что объединение является для участников конфликта целесообразным, так как в этом случае величина выигрыша коалиции увеличивается с увеличением числа вошедших в нее участников. Например, для нашего примера, одного из вариантов перебора, это выражение применимо в виде: V (S {1})+ V (S {2,3})£ V (S È В)= V (I)= V (S {1, 2, 3}). Откуда следует, что в общем случае, справедливо выражение:

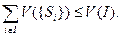
В обозначении V (S_i) заменим на более короткую запись – V (i).

Игра (I, V) называется существенной в том случае, если откуда заключаем, что из разницы 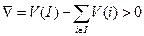возникает дополнительный выигрыш, который может быть распределен между всеми игроками, в результате чего, выигрыш может стать больше для каждого из них, чем в том случае, если каждый из игроков действует самостоятельно.

Игра (I, V) называется несущественной в том случае, если Это означает, что дополнительного выигрыша от объединения всех участников конфликта в коалицию не возникает.

Одним из ключевых понятий в кооперативных играх, это понятие дележа.

Если вектор удовлетворяет условиям:

для всех (14)

(15)

то он называется дележом.

Условие (14) называется условием индивидуальной рациональности, которое предполагает, что объединяться выгодно только в том случае, когда каждый вошедший в коалицию игрок получит при распределении общего выигрыша коалиции, по меньшей мере, столько же, сколько он мог бы получить, действуя самостоятельно, не объединяясь с другими игроками.

Соотношение (15) называется условием коллективной (групповой) рациональности. Он указывает на то, что игроки должны делить между собой реально возможный выигрыш. В нашем примере, соотношение коллективной рациональности будет иметь вид: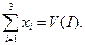

Теорема 1. Для того, чтобы вектор был дележом кооперативной игры необходимо и достаточно выполнение следующего условия: 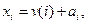где при этом: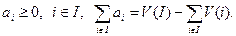

Если игра является существенной, то она может иметь бесконечное множество дележей, и возникает вопрос– как же в этом случае найти решение игры?

Чтобы выявит, какие из множества дележей могут стать решениями игры, вводится понятие доминирования, позволяющее сравнить дележи по предпочтительности.

Дележ Х доминирует дележ Y по коалиции S (отношение доминирования обозначается ), если выполняются следующие соотношения:

– x_i > y_i для всех i Î S, (данное соотношение означает, что дележ Х лучше дележа Y для всех членов коалиции S);

– x (S)£ V (S), (это соотношение означает реальную возможность коалиции S предложить каждому вошедшему в ее состав игроку i Î S величину выигрыша x_i).

Определение 2. Игра называется игрой 0–1 редуцированной форме, если V (i)=0 для всех i Î I, V (I)=1.

Теорема 2. Каждая существенная кооперативная игра эквивалентна некоторой игре в 0–1 редуцированной форме.

Из этой теоремы следует, что существенные игры можно изучать, используя их 0–1 редуцированную (нормализованную) форму.

Если V– характеристическая функция произвольной существенной игры , то

является 0–1 нормализацией, соответствующей функции V.

Для нашего примера, предположим:

V (1)=30; V (2)=50; V (3)=70; V (1,2)=110; V (1,3)=160; V (2,3)=210; V (1,2,3)=450;

Тогда значения этой функции, выраженной в 0–1 редуцированной форме, будут иметь вид:

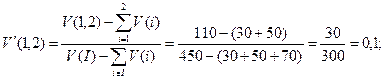
Введем понятие: множество недоминируемых дележей кооперативной игры называется C –ядром.

Теорема 3. Для того, чтобы дележ Х принадлежал C –ядру, необходимо и достаточно выполнение системы неравенств:

для всех S Ì I.

C –ядро является замкнутым выпуклым (возможно пустым) подмножеством множества дележей.

Из теоремы следует, чтобы дележ Х принадлежал C –ядру, необходимо и достаточно выполнение следующих неравенств:

(16)

Решение дележей R кооперативной игры называют решением по Нейману–Моргенштерну (или Н–М решением) если:

– из того, что X > Y, следует, что либо XÏR, либо YÏR;

– для любого XÏR существует такой YÎR, что X > Y.

Теорема 4. Если для игры , характеристическая функция которой представлена 0–1 редуцированной форме, а для 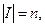выполняются неравенства:

Где число членов в коалиции (I),

число членов в коалиции S,

то C –ядро такой игры не пусто и является Н–М решением.

Н–М решение представляет собой множество таких дележей, которые обладают свойствами:

– внешней устойчивостью, т.е. доминируют любые дележи, которые не принадлежат этому подмножеству (лежат вне этого подмножества);

– внутренней устойчивостью, т.е. дележи, принадлежащие этому подмножеству, не доминируют друг друга.

Покажем, что для нашего примера, C –ядро не пусто, для этого проверим систему неравенств:

Так рассмотренной системе все условия выполняются, следует, что C –ядро рассмотренной кооперативной игры не пусто.

Определим предварительное решение, согласно условию (16):

В качестве решения можно взять вектор

Чтобы найти соответствующий данному решению вектор Х, воспользуемся взаимнооднозначным соответствием множества всех дележей в эквивалентных играх, на основании которого:

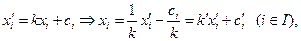
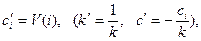
тогда

Таким образом: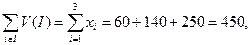что соответствует условию задачи. Полученное решение будет не единственным, так как в данном случае существует множество решений принадлежащих C –ядру, и каждое из них может быть решением рассматриваемой игры.

Задача № 4.5.

Петров, Иванов, Сидоров и Пашков занимаются ремонтом квартир.

В отдельности, каждый в месяц зарабатывает:

1. Петров– 15 тыс. руб.;

2. Иванов– 20 тыс. руб.;

3. Сидоров– 18 тыс. руб.;

4. Пашков– 25 тыс. руб.

Пробуя увеличить заработок, они пробовали работать парами, причем их заработок вместе составил (тыс. руб.):

1 и 2 – 38; 1 и 3 – 35; 1 и 4 – 45; 2 и 3 – 42; 2 и 4 – 50; 3 и 4 – 47(6 вариантов).

Работая по трое, их заработок на группу составил (тыс. руб.):

1, 2 и 3 – 60; 1, 2 и 4 – 70; 1, 3 и 4–65; 2, 3 и 4 – 74 (4 варианта).

Работая всей бригадой, т.е. вчетвером, их заработок в месяц на бригаду составил – 120 тыс. руб.

2 ⁿ =2⁴=16=4(по одному)+6(по два)+4(по трое)+1(вчетвером)+1(Æ)=16.

Необходимо определить, есть ли смысл объединять им свои усилия, и если да, то на каких условиях.

Решение. Решение будем искать, когда одна из групп состоит из 3-х человек.

1. Найдем значение характеристической функции – V (S {1,2,3,4})=120тыс. руб.

2. Необходимо определить, обладает ли характеристическая функция свойством супераддитивности. Необходимо проверить все условия:

V (S {1})+ V (S {2,3,4})< V (S È B)= V (I) Þ 15+74=89<120,

V (S {2})+ V (S {1,3,4})< V (S È B)= V (I) Þ 20+65=85<120,

V (S {3})+ V (S {1,2,4})< V (S È B)= V (I) Þ 18+70=88<120,

V (S {4})+ V (S {1,2,3})< V (S È B)= V (I) Þ 25+60=85<120,

V (S {1,2})+ V (S {3,4})< V (S È B)= V (I) Þ 38+47=85<120,

V (S {1,3})+ V (S {2,4})< V (S È B)= V (I) Þ 35+50=85<120,

V (S {1,4})+ V (S {2,3})< V (S È B)= V (I) Þ 45+42=87<120,

Все условия выполнены, следовательно, наша характеристическая функция является супераддитивной. Это в свою очередь говорит о целесообразности объединения всех игроков, для увеличения выигрыша.

3. Определим, является ли рассматриваемая игра существенной.

неравенство выполняется, следовательно, рассматриваемая нами игра является существенной и ее решение нужно искать среди множества недоминируемых дележей.

4. Представим нашу игру в 0–1 редуцированной форме.

что очевидно, и

Применяя формулу , получим:

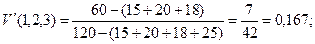
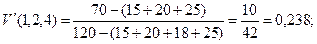
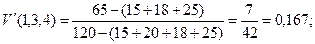
5. Докажем, что C –ядро не пусто.

6. Найдем вектор решения, для 0–1 редуцированной форме системе неравенств:

Этот вектор равен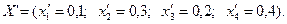

7. Найдем соответствующий вектору X ¢ вектор X.

Таким образом:что соответствует условию задачи.

Ответ:

Петров– 19,2 тыс. руб.(+4,2);

Иванов– 32,6 тыс. руб.(+12,6)

Сидоров– 26,4 тыс. руб.(+8,4);

Пашков– 41,8 тыс. руб.(+16,8).

Дата добавления: 2014-01-07