Итерационный способ вычисления интерполяционного полинома

End.

Begin

Begin

Begin

Begin

Begin

Begin

Begin

Case l of

Begin

Begin

Begin

Begin

Begin

Begin

Begin

Begin

Begin

Implementation

Interface

Пример.

Unit Splin;

{$N+ $E+}

Uses Rtype;

Const Nmax = 50;

Type RealType = Extended;

Vect = Array [1..Nmax] of RealType;

Type SplineInterpolate = object

N1: Integer;

X, Y, M: Vect;

Constructor Init;

procedure Input; Virtual;

procedure NDotSpline(NNN:Integer);

procedure CalculateSpline;

function Interpolate(XX:RealType): RealType;

procedure Output; Virtual;

function GetX(I:Integer): RealType;

function GetY(I:Integer): RealType;

Destructor Done;

end; (* Object SplineInterpolate *)

constructor SplineInterpolate.Init;

Var i: Integer;

for i:=1 to Nmax do X[i]:=0;

for i:=1 to Nmax do Y[i]:=0;

for i:=1 to Nmax do M[i]:=0;

end;

Procedure SplineInterpolate.Input;

Var i: Integer;

WriteLn(' Кубическая сплайн интерполяция-экстраполяция...');

WriteLn(' ===============================================');

WriteLn;

WriteLn('Введите число точек интерполяции N: ');Read(N1);

for i:= 1 to N1 do

WriteLn(' X[',I:2, '], Y[', I:2, '] = '); Read(X[i], Y[i]);

end;

end; (* SplineInterpolate.Input *)

Procedure SplineInterpolate.NDotSpline(NNN:Integer);

N1:=NNN;

end; (* SplineInterpolate.NDotSpline *)

procedure SplineInterpolate.CalculateSpline;

Var R, S, L: Vect;

H, D, F, E, P: RealType;

k: Integer;

D:=X[2]-X[1]; E:=(Y[2]-Y[1])/D;

L[1]:=0; L[N1]:=0; R[1]:=0; R[N1]:=0; S[1]:=0; S[N1]:=0;

for k:=2 to N1-1 do

H:=D; D:=X[k+1]-X[k];

F:=E; E:=(Y[k+1]-Y[k])/D; L[k]:=D/(D+H);

R[k]:=1-L[k]; S[k]:=6*(E-F)/(H+D);

end; (* for *)

for k:=2 to N1-1 do

P:=1/(R[k]*L[k-1]+2); L[k]:=-L[k]*P;

S[k]:=(S[k]-R[k]*S[k-1])*P;

end; (* for *)

M[N1]:=0; L[N1-1]:=S[N1-1];

M[N1-1]:=L[N1-1];

for k:=N1-2 downto 1 do

L[k]:=L[k]*L[k+1]+S[k]; M[k]:=L[k];

end; (* for *)

end; (* Spline.CalculateSpline *)

function SplineInterpolate.Interpolate(XX:RealType): RealType;

Var l, i, j: Integer;

YY, D, H, P, R: RealType;

if XX <= X[1] then l:=-1 else if XX > X[N1] then l:=1 else l:=0;

D:=X[N1]-X[N1-1];

YY:=D*M[N1-1]/6+(Y[N1]-Y[N1-1])/D;

YY:=YY*(XX-X[N1-1])+Y[N1-1];

end;

{i:=1; while XX > X[i] do i:=i+1;}

j:=1; i:=N1;

While j < i-1 do if XX >= X[Trunc((i+j)/2)] then j:=Trunc((i+j)/2)

else i:=Trunc((i+j)/2);

j:=i-1; D:=X[i]-X[j]; H:=XX-X[j]; R:=X[i]-XX;

P:=D*D/6; YY:=(M[j]*R*R*R+M[i]*H*H*H)/6/D;

YY:=YY+((Y[j]-M[j]*P)*R+(Y[i]-M[i]*P)*H)/D;

end;

-1: begin

D:=X[2]-X[1]; YY:=-D*M[2]/6+(Y[2]-Y[1])/D;

YY:=YY*(XX-X[1])+Y[1];

end;

end; (* case *)

Interpolate:=YY;

end; (* Spline.Interpolate *)

procedure SplineInterpolate.Output;

Var XX:RealType;

Write(' XX: '); Read(XX); WriteLn(Interpolate(XX):5:5);

end;

function SplineInterpolate.GetX(I:Integer): RealType;

GetX:=X[I];

end;

function SplineInterpolate.GetY(I:Integer): RealType;

GetY:=Y[I];

end;

Destructor SplineInterpolate.Done;

end;

3.2.13. Кривые Безье. 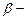сплайны

Важной задачей в машинном проектировании является функциональное описание кривой (или поверхности), заданной графически. Введем множества функций, называемых базисными функциями Бернштейна. Предположим, что все точки данных находятся в интервале 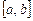. Тогда я базисная функция Бернштейна является полиномом степени 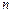вида

.

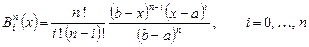Например, для четыре кубические функции базиса Бернштейна имеют вид

На самом деле для вычисления значения берншейновской базисной функции в точке 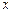определение не применяют. Вместо этого используют рекуррентные формулы

,

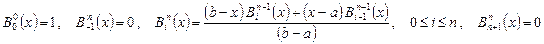которые менее чувствительны к ошибкам округления.

Поскольку каждая функция представляет собой полином степени 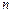, то и их линейная комбинация

является таким же полиномом.

Основная идея – определение графически. С этой целью ставят в соответствие каждому на плоскости точку , которая называется управляющей точкой, при этом 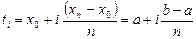. По этим точкам строят ломаную Безье.

Одна трудность, связанная с этим подходом, состоит в том, что невозможно сдвигать управляющие точки вправо или влево. Как только выбрано 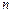, точки фиксируются. Чтобы обеспечить такую возможность, сделаем обобщение. Пусть - точка на плоскости; определить векторную кривую Безье

.

Когда 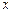изменяется от до , кривая 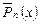описывает траекторию на плоскости, начинающуюся в и кончающуюся в . В этом варианте могут быть произвольными точками, т. е. 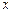- это просто параметр, изменяющийся вдоль кривой.

Для многих приложений полезно уметь записывать интерполянт в виде линейной комбинации функций, которые сами являются сплайнами - это 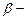сплайны (кусочно-полиномиальная функция с двумя непрерывными производными).

Коэффициенты при 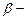сплайнах имеют физическое значение, аналогичное коэффициентам кривой Безье.

(способ Эйткена)

Для линейного интерполирования имеем

(*)

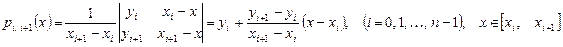В случае, когда точность линейной интерполяции недостаточна, необходимо повышать степень интерполяционного многочлена, привлекая большее число значений .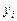

В частности, интерполяционный многочлен второй степени, проходящий через точки , может быть вычислен по формуле

, (**)

где и определены по (*).

Многочлен третьей степени, проходящий через точки , определяется аналогичной формулой

. (***)

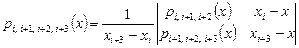Интерполяционный многочлен 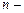й степени, принимающий в точках 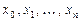соответственно табличные значения , определяется формулой

. (****)

Это и есть итерационный способ Эйткена.

Дата добавления: 2014-01-07