Теорема. Если непрерывна на , то она интегрируема на этом отрезке

Если 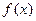непрерывна на 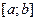, то она интегрируема на этом отрезке.

Замечание.

a) Определенный интеграл – это число. Понятие определенного интеграла вводится через предел интегральных сумм.

b) Неопределенный интеграл - это функция. Понятия неопределенного интеграла вводится через понятие первообразной.

Свойства определенного интеграла:

1) Если 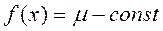, (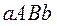- прямоугольник), то

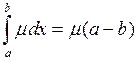
2) Постоянный множитель выносится за знак определенного интеграла

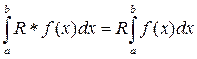
3) Определенный интеграл от алгебраической суммы функции равен алгебраической сумме определенных интегралов от этих функций

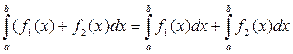
4) Аддитивное свойство.

Отрезок интегрирования можно разбивать на конечное число частей.

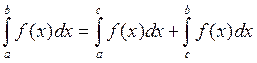
5).

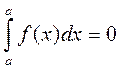
6). Если поменять местами пределы интегрирования, определенный интеграл изменит знак

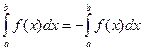
7). Теорема о среднем: Если 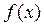непрерывна на отрезке 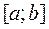, то на этом отрезке найдется такая точка 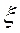, что справедливо

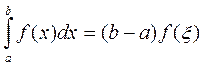
Определенный интеграл с переменным верхним пределом:

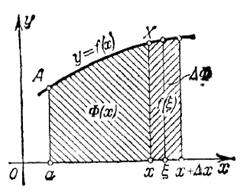
Зафиксируем нижний предел в определенном интеграле, а верхний сделаем изменяющимся. Чтобы не смешивать переменную интегрирования с верхним пределом обозначим ее .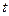

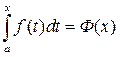
Тогда определенный интеграл станет функцией своего верхнего предела.

Если х дать приращение 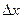, то площадь тоже получит приращение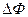

Применим теорему о среднем к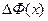

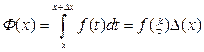, где .

Теорема: Производная определенного интеграла от непрерывной функции с переменным верхним пределом равна подынтегральной функции.

Доказательство: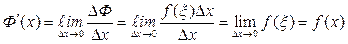

Формула Ньютона – Лейбница

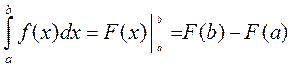
где F(x) - какая-либо первообразная для f(x) – непрерывная.

Примеры: Þ

1).

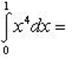
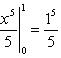
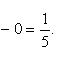
2).

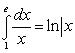
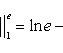
3).

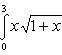
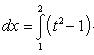
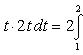
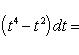
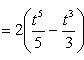
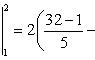
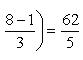
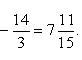
4).

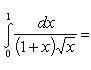
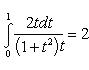
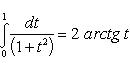
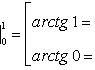
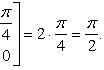
Положим 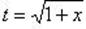, отсюда x = t ² - 1 и dx = 2 t dt. Новые пределы интегрирования определяются из формулы 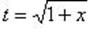; полагая x = 0, будем иметь t = 1 и, полагая x = 3, получим t = 2

Замена переменных в определении интеграла:

Пусть надо вычислить 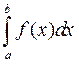, где f (x) непрерывна на [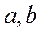] и делается замена

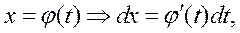
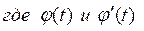определены и непрерывны на 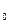[t,T]

Причем

1)

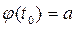
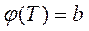
2) F 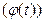определена и непрерывна на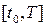

В этом случае справедлива формула:

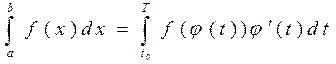
формула аналогична правилу замены переменной в неопределенном интеграле, но здесь надо не забыть заменить старые пределы и b на новые tи Т.

После замены пределов интегрирования возвращение к переменой 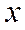не требуется.

Пример:

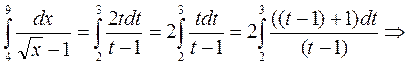
Замена:

;

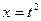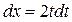
x	t
		(т.к. )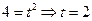
		(т.к. )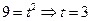

Пример: вычислить площадь эллипса

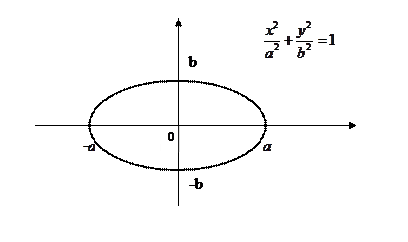
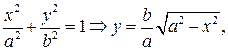для точек 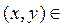I четверти функция однозначна.

Поэтому будем вычислять площадь четверти эллипса

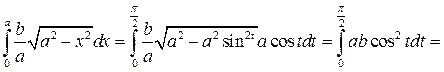
Замена: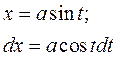

x	t
		(т.к. из )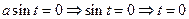
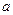
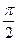
		(т.к. из )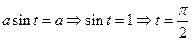

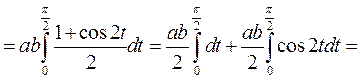
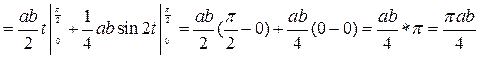
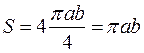
Интегрирование по частям:

Примеры:

1).

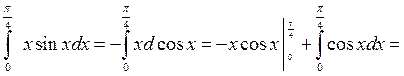
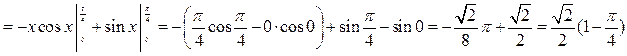
2).

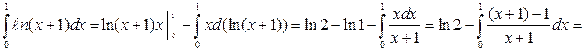
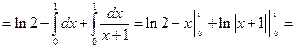
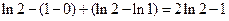
3).

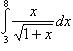
Вычисление площадей

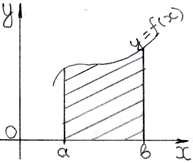
1. Площадь криволинейной трапеции прилежащей к оси ОХ: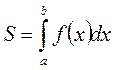

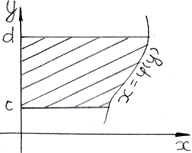
2. Площадь криволинейной трапеции прилежащей к оси ОУ: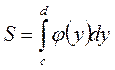

3. Площадь фигуры криволинейной трапеции заданной кривой в параметрическом виде:

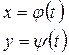
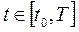
для случая (1):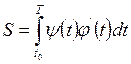

для случая (2):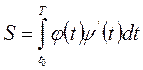

4. Площадь сектора отнесенного к полярной системе координат.

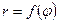
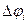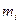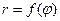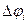Рассмотрим элементарный круговой сектор . Пусть -минимальное значение на ,а 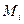-максимальное

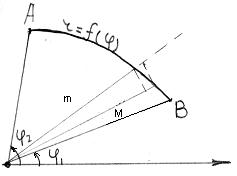
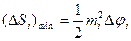
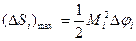
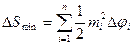
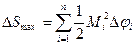
обе эти суммы при мах. 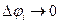стремятся к общему пределу, который равен

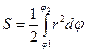
Пример:

1.Вычислить площадь фигуры, ограниченной линиями: ;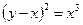

х=1

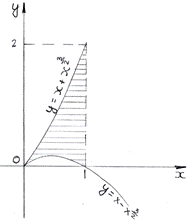
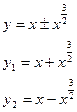
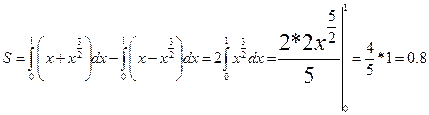
2. Вычислить площадь фигуры, ограниченной кубическими параболами: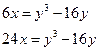

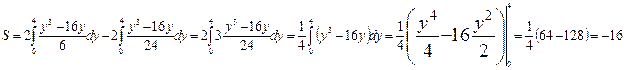
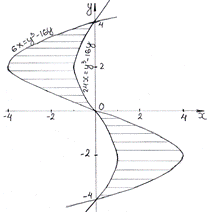
Т.к. площадь не может быть отрицательным, то берем модуль S=16

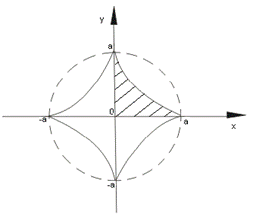
3.вычислить площадь, ограниченную астроидой:

=

-

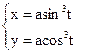
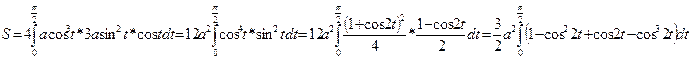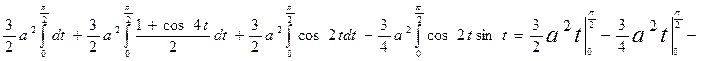
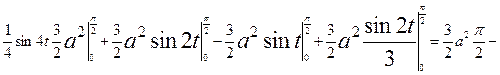
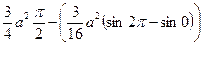
4.Вычислить площадь ограниченную петлей декартового листа: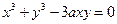

Перейдем к полярной системе координат: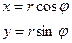

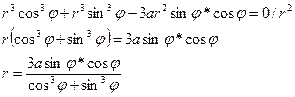
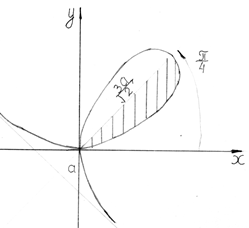
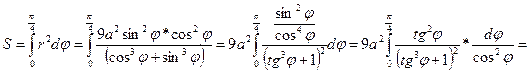(замена: ;

)=

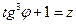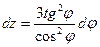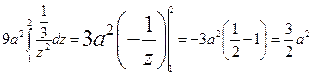
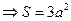
Дата добавления: 2014-01-07