Условия разложения функции в степенной ряд. Ряд Маклорена

Нахождение суммы S (x) данного степенного ряда 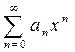называется суммированием степенного ряда.

Нахождение для данной функции f (x) степенного ряда 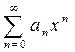, сумма которого есть функция f (x), называется разложением функции f (x) в степенной ряд.

Теорема 1. Если функция f (x) разлагается в степенной ряд, то это разложение единственно.

Доказательство. Пусть в некотором интервале 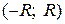функция f (x) является суммой степенного ряда 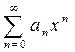, т.е.

.

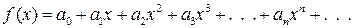Дифференцируем почленно степенной ряд:

.

Дифференцируем почленно полученный степенной ряд:

.

...............................................................

.

...............................................................

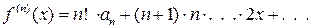Следовательно, , , , …, , ….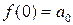

Итак, для каждого n Î N коэффициенты ряда удовлетворяют условию

.

Таким образом, если функция разлагается на некотором интервале в степенной ряд, то это возможно единственным способом, именно:

.

Теорема доказана.

Из теоремы ясно, что разложить в степенной ряд в окрестности точки x =0 можно только функцию, имеющую производную 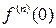любого порядка n Î N.

Определение 1. Пусть функция f (x) имеет в точке x =0 производные любого порядка. Рядом Маклорена функции f (x) называется степенной ряд .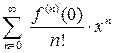

Замечание. Подчеркнем, что теорема 1 является только необходимым условием разложимости функции в степенной ряд. Существуют функции, которые не являются суммами своих рядов Маклорена.

Теорема 2. Пусть функция f (x) имеет производные любого порядка на интервале 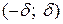и все ее производные ограничены в совокупности, т.е. существует положительное число M >0 такое, что для каждого натурального числа n Î N и для каждого 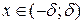выполняется условие .

Тогда сумма ряда Маклорена функции f (x) на интервале 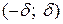есть функция f (x) (без доказательства).

Замечание. На практике применяется несколько способов разложения функции в степенной ряд:

1) для функции f записать ряд Маклорена и доказать его сходимость к функции f;

2) используя известные разложения и применяя линейные операции над рядами и способ замены переменной;

3) используя известные разложения и операции почленного интегрирования и почленного дифференцирования степенных рядов.

3. Разложение в ряд Маклорена функций y = e^x, y =ln(x +1), y =(1+ x) ⁿ.

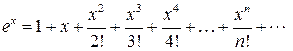, где x Î R.

Заметим, что для любого n Î N и для любого 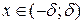выполняется неравенство 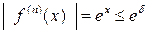, следовательно, по теореме 2, на любом интервале 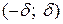(а, значит, на всей числовой прямой) функция e^x равна сумме своего ряда Маклорена.

, где x Î(-1;1].

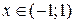На интервале (-1;1) удобно применить известное разложение и применить теорему о почленном интегрировании степенного ряда: . Итак, для любого выполняется .

Можно доказать также, что ряд в точке x =1 имеет сумму ln 2.

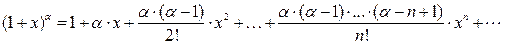, где x Î(-1;1).

Последний ряд называется биномиальным рядом. Известно, что этот ряд сходится в точке 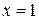при 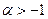, а в точке 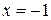абсолютно при .

Составим ряд Маклорена функции y =(1+ x)^a:

y ¢=a×(1+ x)^a^-1	y ¢(0)=a
y ¢¢=a×(a-1)×(1+ x)^a^-2	y ¢¢(0)=a×(a-1)
y ¢¢¢=a×(a-1)×(a-2)×(1+ x)^a^-3	y ¢¢¢(0)=a×(a-1)×(a-2)
…	…
y ^(n)=a×(a-1)×(a-2)×…×(a- n +1)×(1+ x)^a^- n	y ^(n)(0)=a×(a-1)×(a-2)×…×(a- n +1)
…	…

Можно доказать, что ряд 1+имеет суммой функцию y =(1+ x)^a, но это является непростой задачей.

Дата добавления: 2014-01-07