Властивості неперервної функції на відрізку

Теорема 6.6 (Перша теорема Вейєрштрасса). Нехай - неперервна на відрізку , тоді вона обмежена на . Тобто,

.

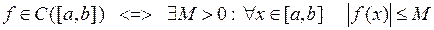Доведення. Від супротивного. Нехай функція неперервна на але не є обмеженою. Тоді для кожного 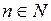знайдеться точка така, що 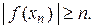Так як послідовність 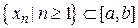,то вона обмежена, і,отже, з неї можна вибрати підпослідовність 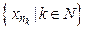збіжну до деякої точки . Так як функція неперервна на ,то вона неперервна і в точці 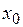, тому , але це неможливо, бо і, отже, при . Таким чином, припущення не вірне. Теорему доведено.

Теорема 6.7 (Друга теорема Вейєрштрасса). Нехай функція неперервна на відрізку , тоді вона приймає на ньому своє найбільше і найменше значення. Тобто, .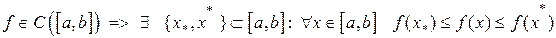

Доведення. Доведемо, наприклад, існування точки , в якій функція приймає своє найменше значення. Так як функція обмежена на , то це означає, що множина 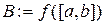значень функції є обмеженою. Тому існує скінчена точна нижня межа множини 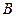, тобто, . Звідки випливає, що

(6.5).

З обмеженої послідовності можна вилучити збіжну підпослідовність 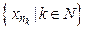, що збігається до деякої точки 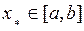. При цьому, з неперервності функції випливає, що а за умовою (6.5), що 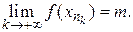Тому, Аналогічно доводиться точки існування відповідної точки . (Довести самостійно!). Теорема доведена.

Теорема 6.8 (Теорема Больцано – Коші). Нехай неперервна на 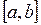, і числ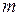а та 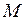є відповідно найменшим і найбільшим значенням функції на відрізку 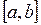. Тоді функція приймає всі проміжні значення між 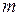та 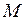. Тобто,

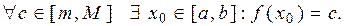
Доведення. Якщ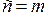о або , то тоді твердження даної теореми випливає з попередньої теореми.

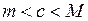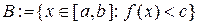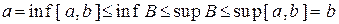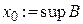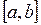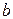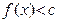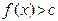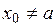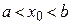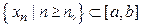Нехай . Розглянемо множину . Так як , то . Отже, точка належить відрізку . За теоремою про збереження знака нерівності функцією при переході до границі слідує, що знайдуться деякі околи точок і , в яких зберігаються нерівності та відповідно. Тому, і , тобто, . За теоремою про характеризацію точних меж для довільного числа починаючи з деякого знайдеться точка така, що . Тому, послідовність збігається до точки 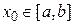, і при цьому . Отже, за неперервністю функції , існує границя . 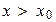Але для всіх точок має місце нерівність 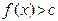, тому, 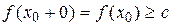. Отже, 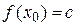, що і потрібно було довести.

Означення 6.6. Функція називається рівномірно неперервною на множині, якщо для довільного числа 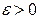знайдеться таке число 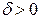, що для всіх точок х і у цієї множини з нерівності слідує , тобто, коли 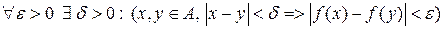(6.6).

Завдання для самостійної роботи 6.4: Довести, що функція рівномірно неперервна на множинітоді і тільки тоді, коли .

Теорема 6.9 (Теорема Кантора). Нехай функціянеперервна на 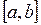, тоді вона рівномірно неперервна на цьому відрізку.

Доведення. Від супротивного. Припустимо, що 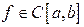, але не є рівномірно неперервною на 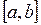. Тоді, за запереченням (6.6) існує таке число 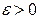, що для будь-якого числа 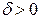, наприклад для , знайдуться такі точки , відстань міх якими менша за число , та при цьому відстань між значеннями функції у ціх точках не менша за число 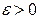. Тобто,

.

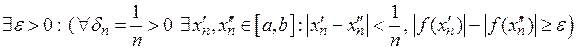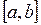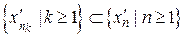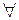
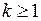
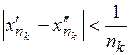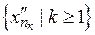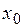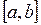Але, послідовність є підмножиною відрізка і,отже, обмежена. Тому з неї можна вилучити підпослідовність , яка збігається до деякого числа при . Так як, , то можна зробити висновок, що і підпослідовність збіжна до при (довести самостійно!). Отже, згідно неперервності на маємо

.

Що неможливо внаслідок нерівності .

Значить, припущення невірне. Теорему доведено.

Дата добавления: 2014-01-07