
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Момент инерции. Уравнение динамики вращательного движения твердого тела вокруг неподвижной оси
|
|
|
|
Величина, равная произведению массы точки и квадрата расстояния от нее до оси вращения, называется моментом инерции точки относительно этой оси
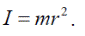
При использовании момента силы и момента инерции равенство принимает вид
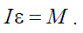
Сравнивая это выражение со вторым законом Ньютона для поступательного движения, приходим к выводу, что при описании вращательного движения с помощью углового ускорения роль массы выполняет момент инерции, а роль силы – момент силы.
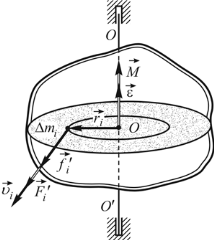
Установим теперь связь между угловым ускорением и моментом сил, действующих на тело, вращающееся вокруг неподвижной оси (рис.5).
|
Разобьем мысленно тело на малые элементы массами 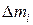 , которые можно считать материальными точками, т.е. будем рассматривать твердое тело как систему материальных точек с неизменными расстояниями между ними. При вращении тела вокруг неподвижной оси
, которые можно считать материальными точками, т.е. будем рассматривать твердое тело как систему материальных точек с неизменными расстояниями между ними. При вращении тела вокруг неподвижной оси 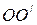 его точки двигаются по окружностям радиусов
его точки двигаются по окружностям радиусов  , которые лежат в плоскостях, перпендикулярных оси вращения.
, которые лежат в плоскостях, перпендикулярных оси вращения.
Пусть на каждую точку действует внешняя сила  и сумма внутренних сил
и сумма внутренних сил  со стороны остальных частиц системы.
со стороны остальных частиц системы.
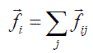
Поскольку точки движутся по плоским окружностям с тангенциальными ускорениями 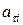 , то это ускорение вызывают касательные составляющие сил
, то это ускорение вызывают касательные составляющие сил  и
и 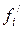 .
.
Запишем второй закон Ньютона для тангенциального ускорения i - й точки
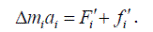
Умножив обе части последнего равенства на  и выразив тангенциальные ускорения точек через угловое (
и выразив тангенциальные ускорения точек через угловое ( ), одинаковое для всех точек тела, получим:
), одинаковое для всех точек тела, получим:
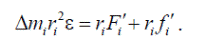
Просуммируем по всем точкам системы, учитывая, что сумма моментов всех внутренних сил равна нулю. Действительно, все внутренние силы можно сгруппировать на попарно равные и противоположно направленные. Силы каждой пары лежат на одной прямой, поэтому имеют одинаковые плечи, а значит равные, но противоположно направленные моменты. В результате получаем уравнение вращательного движения твердого тела вокруг неподвижной оси как системы материальных точек
|
|
|
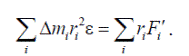
Сумма моментов внешних сил, действующих на тело, равна моменту результирующей этих сил относительно оси OO ′:
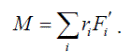
Моментом инерции тела относительно некоторой оси называют сумму моментов инерции всех его точек относительно той же оси:
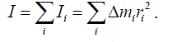
С учетом полученных соотношений, определяющих понятия момента инерции тела  и суммарного момента сил M, имеем:
и суммарного момента сил M, имеем:
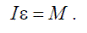
Это выражение называют уравнением динамики вращательного движения твердого тела вокруг неподвижной оси. Вектор углового ускорения тела 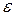 совпадает по направлению с вектором момента сил M относительно неподвижной оси, а момент инерции тела – величина скалярная, следовательно, предыдущее уравнение можно записать в векторной форме:
совпадает по направлению с вектором момента сил M относительно неподвижной оси, а момент инерции тела – величина скалярная, следовательно, предыдущее уравнение можно записать в векторной форме:
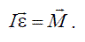
Из этого уравнения можно выразить угловое ускорение
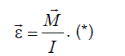
Полученное уравнение (*) называют вторым законом Ньютона для вращательного движения твердого тела. Отличие от поступательного движения заключается в том, что вместо линейного ускорения 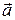 используется угловое
используется угловое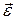 , роль силы
, роль силы 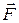 выполняет момент силы
выполняет момент силы  , а роль массы
, а роль массы  – момент инерции
– момент инерции  .
.
В динамике поступательного движения равными силами считаются те, которые сообщают телам равной массы одинаковые ускорения. При вращательном движении одна и та же сила может сообщать телу разные угловые ускорения в зависимости от того, как далеко лежит линия действия силы от оси вращения. Поэтому, например, велосипедное колесо легче привести в движение, прикладывая силу к ободу, чем к середине спицы. Разные тела получают под действием одинаковых моментов сил одинаковые угловые ускорения, если равны их моменты инерции. Момент инерции зависит от массы и ее распределения относительно оси вращения. Поскольку угловое ускорение обратно пропорционально моменту инерции, то при прочих равных условиях тело легче привести в движение, если его масса сконцентрирована ближе к оси вращения.
|
|
|
5. Момент инерции частицы и твердых тел: стержня, цилиндра, диска, шара
Каждое тело независимо от того, вращается оно или находится в состоянии покоя, обладает определенным моментом инерции относительно любой выбранной оси подобно тому, как тело имеет массу независимо от его состояния движения или покоя. Таким образом, момент инерции является мерой инертности тела при вращательном движении. Очевидно, что проявляется момент инерции только тогда, когда на тело начинает действовать момент внешних сил, который вызывает угловое ускорение. Согласно определению момент инерции – величина аддитивная. Это означает, что момент инерции тела относительно некоторой оси равен сумме моментов инерции отдельных его частей. Отсюда следует метод расчета моментов инерции тел.
Для вычисления момента инерции необходимо мысленно разбить тела на достаточно малые элементы 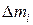 , точки которых лежат на одинаковом расстоянии
, точки которых лежат на одинаковом расстоянии  от оси вращения, затем найти произведение массы каждого элемента и квадрата его расстояния до оси и, наконец, просуммировать все произведения. Чем больше элементов берется, тем точнее метод. В случае, когда тело разбивается на бесконечно большое количество бесконечно малых элементов
от оси вращения, затем найти произведение массы каждого элемента и квадрата его расстояния до оси и, наконец, просуммировать все произведения. Чем больше элементов берется, тем точнее метод. В случае, когда тело разбивается на бесконечно большое количество бесконечно малых элементов  , суммирование заменяется интегрированием по всему объему тела
, суммирование заменяется интегрированием по всему объему тела
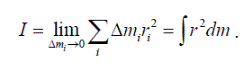
Для тела с неравномерным распределением массы формула дает среднюю плотность.
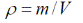
В этом случае плотность в данной точке определяется как предел отношения массы бесконечно малого элемента 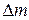 к его объему
к его объему 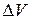
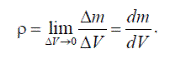
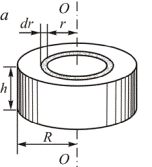
Расчет момента инерции произвольных тел является довольно трудоемкой задачей. Приведем в качестве примера вычисление моментов инерции некоторых однородных тел правильной геометрической формы относительно их осей симметрии. Вычислим момент инерции сплошного цилиндра (диска) радиусом R, толщиной h и массой m относительно оси, проходящей через центр перпендикулярно основанию цилиндра. Разобьем цилиндр на тонкие кольцевые слои радиусом r и толщиной dr (рис.6, а).
|
|
|
|
Поскольку 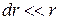 , то можем считать, что расстояние всех точек слоя от оси равно r. Для каждого отдельного такого кольцевого слоя момент инерции
, то можем считать, что расстояние всех точек слоя от оси равно r. Для каждого отдельного такого кольцевого слоя момент инерции
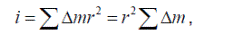
где  – масса всего слоя. Объем слоя (
– масса всего слоя. Объем слоя (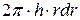 ), где h – высота слоя. Если плотность материала цилиндра ρ, то масса слоя будет равна
), где h – высота слоя. Если плотность материала цилиндра ρ, то масса слоя будет равна
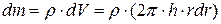
Для вычисления момента инерции цилиндра необходимо просуммировать моменты инерции слоев от центра цилиндра (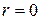 ), до его края (
), до его края ( ), т.е. вычислить интеграл:
), т.е. вычислить интеграл:
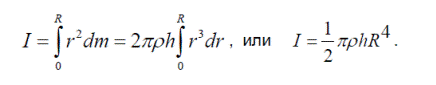
С учетом того, что масса цилиндра
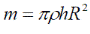
получим:
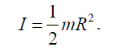
Приведем без вывода (вывод см. Яворский и Детлаф, можно см. Савельева (т.1), основные формулы содержатся и в моем пособии (но без вывода)) моменты инерции некоторых других тел, выполненных из однородных материалов, часто встречающиеся при решении задач.
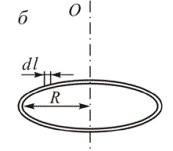
1. Момент инерциитонкого кольца относительно оси, проходящей через центр симметрии перпендикулярно плоскости кольца (рис.6, б)
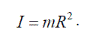
|
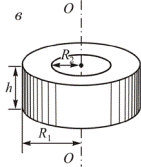
2. Момент инерции толстостенного цилиндра массой  и радиусами
и радиусами  и
и  относительно оси симметрии (рис.6, в)
относительно оси симметрии (рис.6, в)
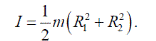
|
3. Момент инерции диска относительно оси, совпадающей с его диаметром, (рис.6, г)
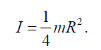
|
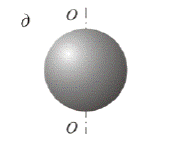
4. Момент инерции шара относительно оси, совпадающей с его диамет-ром, (рис.6, д)
|
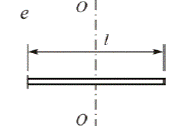
5. Момент инерции тонкого стержня длиной l и массой m относительно оси, проходящей через его центр перпендикулярно стержню, (рис.6, е)
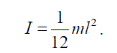
|
|
|
|
|
|
Дата добавления: 2014-01-07; Просмотров: 7162; Нарушение авторских прав?; Мы поможем в написании вашей работы!