
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Градиентные методы
|
|
|
|
Лекция № 8
Градиентные методы решения задач нелинейного программирования. Методы штрафных функций. Приложения нелинейного программирования к задачам исследования операций.
Задачи без ограничений. Градиентным методом можно решать, вообще говоря, любую нелинейную задачу. Однако при этом находится лишь локальный экстремум. Поэтому целесообразнее применять этот метод при решении задач выпуклого программирования, в которых любой локальный экстремум, является одновременно и глобальным (см. теорему 7.6).
Будем рассматривать задачу максимизации нелинейной дифференцируемой функции f (x). Суть градиентного поиска точки максимума х * весьма проста: надо взять произвольную точку х 0 и с помощью градиента 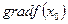 , вычисленного в этой точке, определить направление, в котором f (х) возрастает с наибольшей скоростью (рис. 7.4),
, вычисленного в этой точке, определить направление, в котором f (х) возрастает с наибольшей скоростью (рис. 7.4),
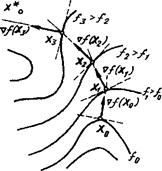
Рис. 7.4
а затем, сделав небольшой шаг в найденном направлении, перейти в новую точку xi. Потом снова определить наилучшее направление 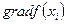 для перехода в очередную точку х 2 и т. д. На рис. 7.4 поисковая траектория представляет собой ломаную х 0, x 1, х 2... Таким образом, надо построить последовательность точек х 0, x 1, х 2,..., x k,... так, чтобы она сходилась к точке максимума х *, т. е. для точек последовательности выполнялись условия
для перехода в очередную точку х 2 и т. д. На рис. 7.4 поисковая траектория представляет собой ломаную х 0, x 1, х 2... Таким образом, надо построить последовательность точек х 0, x 1, х 2,..., x k,... так, чтобы она сходилась к точке максимума х *, т. е. для точек последовательности выполнялись условия
Градиентные методы, как правило, позволяют получать точное решение за бесконечное число шагов и только в некоторых случаях — за конечное. В связи с этим градиентные методы относят к приближенным методам решения.
Движение из точки хk в новую точку xk+1 осуществляется по прямой, проходящей через точку хk и имеющей уравнение
 (7.29)
(7.29)
где λk — числовой параметр, от которого зависит величина шага. Как только значение параметра в уравнении (7.29) выбрано: λk=λk0, так становится определенной очередная точка 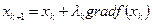 на поисковой ломаной.
на поисковой ломаной.
|
|
|
Градиентные методы отличаются друг от друга способом выбора величины шага — значения λk0 параметра λk. Можно, например, двигаться из точки в точку с постоянным шагом λk= λ, т. е. при любом k
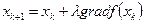 .
.
Если при этом окажется, что 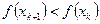 , то следует возвратиться в точку
, то следует возвратиться в точку 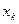 и уменьшить значение параметра, например до λ /2.
и уменьшить значение параметра, например до λ /2.
Иногда величина шага берется пропорциональной модулю градиента.
Если ищется приближенное решение, то поиск можно прекратить, основываясь на следующих соображениях. После каждой серии из определенного числа шагов сравнивают достигнутые значения целевой функции f (x). Если после очередной серии изменение f (x) не превышает некоторого наперед заданного малого числа 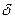 , поиск прекращают и достигнутое значение f (x) рассматривают как искомый приближенный максимум, а соответствующее ему х принимают за х *.
, поиск прекращают и достигнутое значение f (x) рассматривают как искомый приближенный максимум, а соответствующее ему х принимают за х *.
Если целевая функция f (x) вогнутая (выпуклая), то необходимым и достаточным условием оптимальности точки х * является равенство нулю градиента функции в этой точке.
Распространенным является вариант градиентного поиска, называемый методом наискорейшего подъема. Суть его в следующем. После определения градиента 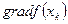 в точке хк движение вдоль прямой
в точке хк движение вдоль прямой 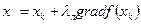 производится до точки хк+ 1, в которой достигается максимальное значение функции f (х) в направлении градиента
производится до точки хк+ 1, в которой достигается максимальное значение функции f (х) в направлении градиента 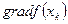 . Затем в этой точке вновь определяется градиент, и движение совершается по прямой
. Затем в этой точке вновь определяется градиент, и движение совершается по прямой 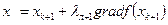 в направлении нового градиента
в направлении нового градиента 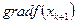 до точки хк+ 2, в которой достигается максимальное в этом направлении значение f (x). Движение продолжается до тех пор, пока не будет достигнута точка х *, соответствующая наибольшему значению целевой функции f (x). На рис. 7.5 приведена схема движения к оптимальной точке х * методом наискорейшего подъема. В данном случае направление градиента
до точки хк+ 2, в которой достигается максимальное в этом направлении значение f (x). Движение продолжается до тех пор, пока не будет достигнута точка х *, соответствующая наибольшему значению целевой функции f (x). На рис. 7.5 приведена схема движения к оптимальной точке х * методом наискорейшего подъема. В данном случае направление градиента 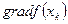 в точке хk является касательным к линии уровня поверхности f (х) в точке хк+ 1, следовательно, градиент
в точке хk является касательным к линии уровня поверхности f (х) в точке хк+ 1, следовательно, градиент 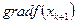 в точке хк+ 1 ортогонален градиенту
в точке хк+ 1 ортогонален градиенту 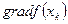 (сравните с рис. 7.4).
(сравните с рис. 7.4).
|
|
|
Перемещение из точки хk в точку 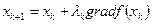 сопровождается возрастанием функции f (x) на величину
сопровождается возрастанием функции f (x) на величину
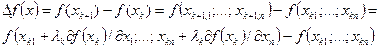 (7.30)
(7.30)
Из выражения (7.30) видно, что приращение 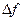 является функцией переменной
является функцией переменной 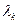 , т. е.
, т. е. 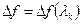 . При нахождении максимума функции f (x) в направлении градиента
. При нахождении максимума функции f (x) в направлении градиента 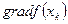 ) необходимо выбирать шаг перемещения (множитель
) необходимо выбирать шаг перемещения (множитель 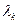 ), обеспечивающий наибольшее возрастание приращению функции, именно функции
), обеспечивающий наибольшее возрастание приращению функции, именно функции 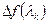 . Величина
. Величина 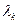 , при которой достигается наибольшее значение
, при которой достигается наибольшее значение 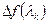 , может быть определена из необходимого условия экстремума функции
, может быть определена из необходимого условия экстремума функции 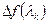 :
:
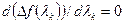 (7.31)
(7.31)
Найдем выражение для производной, дифференцируя равенство (7.30) по 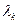 как сложную функцию:
как сложную функцию:
 Подставляя этот результат в равенство (7.31), получаем
Подставляя этот результат в равенство (7.31), получаем
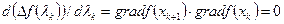 (7.32)
(7.32)
Это равенство имеет простое геометрическое истолкование: градиент в очередной точке хк+ 1, ортогонален градиенту в предыдущей точке хк.
 |
Пример 7.4. Определить максимум функции
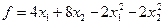 , начав оптимизационный поиск с точки
, начав оптимизационный поиск с точки 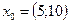 .
.
Решение. Будем сопровождать решение задачи графической иллюстрацией (рис. 7.6). По данному уравнению параболоида вращения
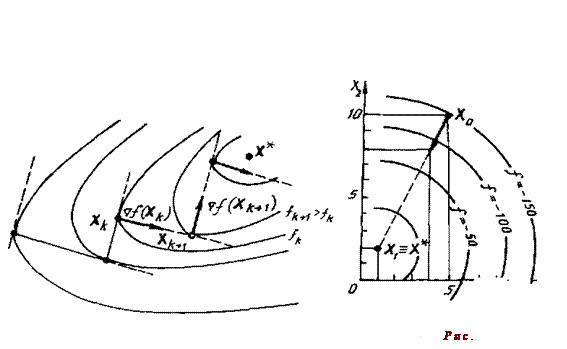 |
построены линии уровня этой поверхности. С этой целью уравнение приведено к виду (x 1-1)2+(x2-2)2=5-0,5 f, из которого ясно, что линиями пересечения параболоида с плоскостями, параллельными плоскости x 1О x 2 (линиями уровня), являются окружности радиусом
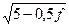 . При f =-150, -100, -50 их радиусы равны соответственно
. При f =-150, -100, -50 их радиусы равны соответственно 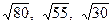 , а общий центр находится в точке (1; 2). Находим градиент данной функции:
, а общий центр находится в точке (1; 2). Находим градиент данной функции:
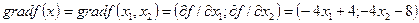 .
.
I шаг. Вычисляем:

На рис. 7.6 с началом в точке х 0=(5; 10) построен вектор 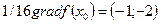 1/16, указывающий направление наискорейшего возрастания функции в точке х 0. На этом направлении расположена следующая точка
1/16, указывающий направление наискорейшего возрастания функции в точке х 0. На этом направлении расположена следующая точка 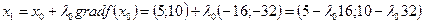 . В этой точке
. В этой точке 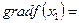
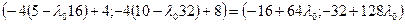 .
.
Используя условие (7.32), получаем
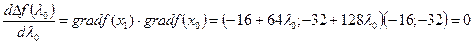
или 1-4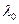 =0, откуда
=0, откуда 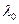 =1/4. Так как
=1/4. Так как 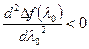 , то найденное значение
, то найденное значение 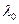 является точкой максимума
является точкой максимума 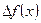 . Находим x 1=(5-16/4; 10-32/4)=(1; 2).
. Находим x 1=(5-16/4; 10-32/4)=(1; 2).
II шаг. Начальная точка для второго шага x 1=(1; 2). Вычисляем 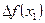 =(-4∙1 +4; -4∙2+8)=(0; 0). Следовательно, х 1=(1; 2) является стационарной точкой. Но поскольку данная функция вогнутая, то в найденной точке (1; 2) достигается глобальный максимум.
=(-4∙1 +4; -4∙2+8)=(0; 0). Следовательно, х 1=(1; 2) является стационарной точкой. Но поскольку данная функция вогнутая, то в найденной точке (1; 2) достигается глобальный максимум.
Задача с линейными ограничениями. Сразу же отметим, что если целевая функция f (х) в задаче с ограничениями имеет единственный экстремум и он находится внутри допустимой области, то для поиска экстремальной точки х * применяется изложенная выше методика без каких-либо изменений.
|
|
|
Рассмотрим задачу выпуклого программирования с линейными ограничениями:
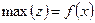 (7.33)
(7.33)
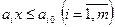 (7.34)
(7.34)
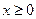 (7.35)
(7.35)
где 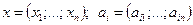 .
.
Предполагается, что f (х) является вогнутой функцией и имеет непрерывные частные производные в каждой точке допустимой области.
Начнем с геометрической иллюстрации процесса решения задачи (рис. 7.7). Пусть начальная точка х 0 расположена внутри допустимой области. Из точки х 0 можно двигаться в направлении градиента 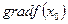 , пока f (x) не достигнет максимума. В нашем случае f (x) все время возрастает, поэтому остановиться надо в точке х, на граничной прямой. Как видно из рисунка, дальше двигаться в направлении градиента
, пока f (x) не достигнет максимума. В нашем случае f (x) все время возрастает, поэтому остановиться надо в точке х, на граничной прямой. Как видно из рисунка, дальше двигаться в направлении градиента 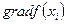 нельзя, так как выйдем из допустимой области. Поэтому надо найти другое направление перемещения, которое, с одной стороны, не выводит из допустимой области, а с другой — обеспечивает наибольшее возрастание f (x). Такое направление определит вектор
нельзя, так как выйдем из допустимой области. Поэтому надо найти другое направление перемещения, которое, с одной стороны, не выводит из допустимой области, а с другой — обеспечивает наибольшее возрастание f (x). Такое направление определит вектор 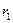 , составляющий с вектором
, составляющий с вектором 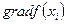 наименьший острый угол по сравнению с любым другим вектором, выходящим из точки xi и лежащим в допустимой области. Аналитически такой вектор найдется из условия максимизации скалярного произведения
наименьший острый угол по сравнению с любым другим вектором, выходящим из точки xi и лежащим в допустимой области. Аналитически такой вектор найдется из условия максимизации скалярного произведения 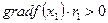 . В данном случае вектор
. В данном случае вектор 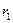 указывающий наивыгоднейшее направление, совпадает с граничной прямой.
указывающий наивыгоднейшее направление, совпадает с граничной прямой.
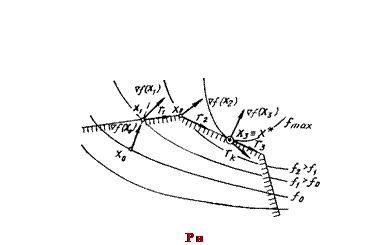 |
Таким образом, на следующем шаге двигаться надо по граничной прямой до тех пор, пока возрастает f (x); в нашем случае — до точки х 2. Из рисунка видно, что далее следует перемещаться в направлении вектора
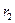 , который находится из условия максимизации скалярного произведения
, который находится из условия максимизации скалярного произведения  , т. е. по граничной прямой. Движение заканчивается в точке х 3, поскольку в этой точке завершается оптимизационный поиск, ибо в ней функция f (х) имеет локальный максимум. Ввиду вогнутости в этой точке f (х) достигает также глобального максимума в допустимой области. Градиент в точке максимума х 3= х * составляет тупой угол с любым вектором
, т. е. по граничной прямой. Движение заканчивается в точке х 3, поскольку в этой точке завершается оптимизационный поиск, ибо в ней функция f (х) имеет локальный максимум. Ввиду вогнутости в этой точке f (х) достигает также глобального максимума в допустимой области. Градиент в точке максимума х 3= х * составляет тупой угол с любым вектором  из допустимой области, проходящим через х3, поэтому скалярное произведение
из допустимой области, проходящим через х3, поэтому скалярное произведение 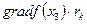 будет отрицательным для любого допустимого rk, кроме r 3, направленного по граничной прямой. Для него скалярное произведение
будет отрицательным для любого допустимого rk, кроме r 3, направленного по граничной прямой. Для него скалярное произведение 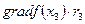 =0, так как
=0, так как 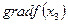 и
и  взаимно перпендикулярны (граничная прямая касается линии уровня поверхности f (х), проходящей через точку максимума х *). Это равенство и служит аналитическим признаком того, что в точке х 3 функция f (x) достигла максимума.
взаимно перпендикулярны (граничная прямая касается линии уровня поверхности f (х), проходящей через точку максимума х *). Это равенство и служит аналитическим признаком того, что в точке х 3 функция f (x) достигла максимума.|
|
|
Рассмотрим теперь аналитическое решение задачи (7.33) — (7.35). Если оптимизационный поиск начинается с точки, лежащей в допустимой области (все ограничения задачи выполняются как строгие неравенства), то перемещаться следует по направлению градиента так, как установлено выше. Однако теперь выбор λk в уравнении (7.29) усложняется требованием, чтобы очередная точка 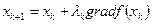 оставалась в допустимой области. Это означает, что ее координаты должны удовлетворять ограничениям (7.34), (7.35), т. е. должны выполняться неравенства:
оставалась в допустимой области. Это означает, что ее координаты должны удовлетворять ограничениям (7.34), (7.35), т. е. должны выполняться неравенства:
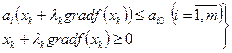 (7.36)
(7.36)
Решая систему линейных неравенств (7.36), находим отрезок 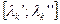 допустимых значений параметра λk, при которых точка хk+1 будет принадлежать допустимой области.
допустимых значений параметра λk, при которых точка хk+1 будет принадлежать допустимой области.
Значение λk*, определяемое в результате решения уравнения (7.32):
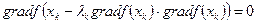 , при котором f (x) имеет локальный максимум по λk в направлении
, при котором f (x) имеет локальный максимум по λk в направлении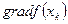 , должно принадлежать отрезку
, должно принадлежать отрезку 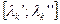 . Если же найденное значение λk выходит за пределы указанного отрезка, то в качестве λk* принимается
. Если же найденное значение λk выходит за пределы указанного отрезка, то в качестве λk* принимается 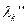 . В этом случае очередная точка поисковой траектории оказывается на граничной гиперплоскости, соответствующей тому неравенству системы (7.36), по которому при решении системы получена правая конечная точка
. В этом случае очередная точка поисковой траектории оказывается на граничной гиперплоскости, соответствующей тому неравенству системы (7.36), по которому при решении системы получена правая конечная точка 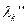 . отрезка допустимых значений параметра λk.
. отрезка допустимых значений параметра λk.
Если оптимизационный поиск начат с точки, лежащей на граничной гиперплоскости, или очередная точка поисковой траектории оказалась на граничной гиперплоскости, то для продолжения движения к точке максимума прежде всего необходимо найти наилучшее направление движения С этой целью следует решить вспомогательную задачу математического программирования, а именно- максимизировать функцию
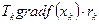 (7.37)
(7.37)
при ограничениях
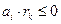 (7.38)
(7.38)
для тех t, при которых
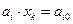 (7.39)
(7.39)
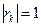 (7.40)
(7.40)
где 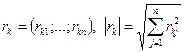 .
.
В результате решения задачи (7.37) — (7.40) будет найден вектор 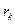 , составляющий с градиентом наименьший острый угол.
, составляющий с градиентом наименьший острый угол.
Условие (7.39) говорит о том, что точка 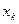 принадлежит границе допустимой области, а условие (7.38) означает, что перемещение из
принадлежит границе допустимой области, а условие (7.38) означает, что перемещение из 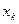 по вектору
по вектору 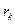 будет направлено внутрь допустимой области или по ее границе. Условие нормализации (7.40) необходимо для ограничения величины
будет направлено внутрь допустимой области или по ее границе. Условие нормализации (7.40) необходимо для ограничения величины 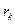 , так как в противном случае значение целевой функции (7.37) можно сделать сколь угодно большим Известны различные формы условий нормализации, и в зависимости от этого задача (7.37) — (7.40) может быть линейной или нелинейной.
, так как в противном случае значение целевой функции (7.37) можно сделать сколь угодно большим Известны различные формы условий нормализации, и в зависимости от этого задача (7.37) — (7.40) может быть линейной или нелинейной.
После определения направления 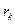 находится значение λk* для следующей точки
находится значение λk* для следующей точки 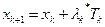 поисковой траектории. При этом используется необходимое условие экстремума в форме, аналогичной уравнению (7.32), но с заменой
поисковой траектории. При этом используется необходимое условие экстремума в форме, аналогичной уравнению (7.32), но с заменой 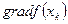 на вектор
на вектор 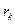 , т. е.
, т. е.
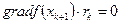 (7.41)
(7.41)
Оптимизационный поиск прекращается, когда достигнута точка xk*, в которой 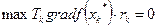 .
.
Пример 7.5. Максимизировать функцию 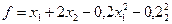 при ограничениях
при ограничениях
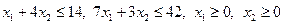 .
.
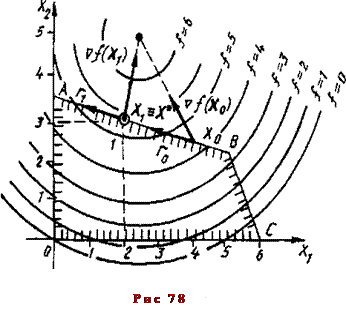
Решение. Для наглядного представления процесса оптимизации будем сопровождать его графической иллюстрацией. На рис 7.8 изображено несколько линий уровня данной поверхности и допустимая область ОАВС, в которой следует найти точку х *, доставляющую максимум данной функции (см. пример 7 4).
Начнем оптимизационный поиск, например с точки х 0=(4, 2,5), лежащей на граничной прямой АВ x 1+4 x 2=14. При этом f (х 0)=4,55.
Найдем значение градиента
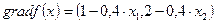 в точке x 0
в точке x 0 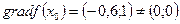 . Кроме того, и по рисунку видно, что через допустимую область проходят линии уровня с пометками более высокими, чем f (x 0)=4,55. Словом, надо искать направление r 0=(r 01, r 02) перемещения в следующую точку x 1 более близкую к оптимальной. С этой целью решаем задачу (7.37) — (7.40) максимизации функции
. Кроме того, и по рисунку видно, что через допустимую область проходят линии уровня с пометками более высокими, чем f (x 0)=4,55. Словом, надо искать направление r 0=(r 01, r 02) перемещения в следующую точку x 1 более близкую к оптимальной. С этой целью решаем задачу (7.37) — (7.40) максимизации функции 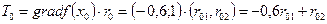 при ограничениях
при ограничениях
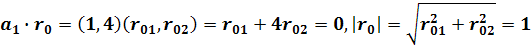
 |
Поскольку точка х 0 располагается только на одной (первой) граничной прямой (i =1) x 1+4 x 2=14, то условие (7.38) записывается в форме равенства.
Система ограничительных уравнений этой задачи имеет только два решения (-0,9700; 0,2425) и (0,9700;-0,2425) Непосредственной подстановкой их в функцию T 0 устанавливаем, что максимум Т 0 отличен от нуля и достигается при решении (-0,9700; 0,2425) Таким образом, перемещаться из х 0 нужно по направлению вектора r 0=(0,9700; 0,2425), т е по граничной прямой ВА.
Для определения координат следующей точки x 1=(x 11; x 12)
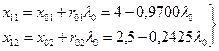 (7.42)
(7.42)
необходимо найти значение параметра 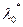 , при котором функция f (x) в точке x 1 достигает возможно большего значения. Но сначала найдем интервал допустимых значений параметра
, при котором функция f (x) в точке x 1 достигает возможно большего значения. Но сначала найдем интервал допустимых значений параметра 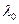 , при которых точка x 1 будет принадлежать допустимой области. Система (7.36) в данном случае имеет вид
, при которых точка x 1 будет принадлежать допустимой области. Система (7.36) в данном случае имеет вид
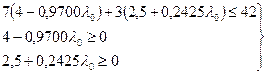 (7.43)
(7.43)
Первое ограничение мы опустили, поскольку точка x 1 лежит на прямой АВ. Решая систему (7.43), устанавливаем, что 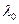 следует искать в полуинтервале (0; 4,1237] (заметим, что нас интересуют только не отрицательные значения параметра
следует искать в полуинтервале (0; 4,1237] (заметим, что нас интересуют только не отрицательные значения параметра 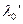 ). Найдем значение
). Найдем значение 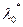 , при котором достигается наибольшее возрастание приращения
, при котором достигается наибольшее возрастание приращения 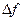 функции, вы званное перемещением из точки x 0 в точку x 1. В соответствии с условием (7.41)
функции, вы званное перемещением из точки x 0 в точку x 1. В соответствии с условием (7.41)
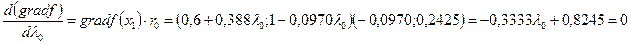 ,
,
откуда 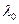 =2,0618. При этом
=2,0618. При этом 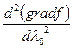 =-0,3999<0. Значит,
=-0,3999<0. Значит,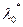 =2,0618. По формуле (7.42) находим координаты новой точки х1 (2; 3).
=2,0618. По формуле (7.42) находим координаты новой точки х1 (2; 3).
Если продолжить оптимизационный поиск, то при решении очередной вспомогательной задачи (7.37)— (7.40) будет установлено, что Т1=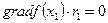 , а это говорит о том, что точка x1 является точкой максимума х* целевой функции в допустимой области. Это же видно и из рисунка в точке x1 одна из линий уровня касается границы допустимой области. Следовательно, точка x1 является точкой максимума х*. При этом f max= f (x *)=5,4.
, а это говорит о том, что точка x1 является точкой максимума х* целевой функции в допустимой области. Это же видно и из рисунка в точке x1 одна из линий уровня касается границы допустимой области. Следовательно, точка x1 является точкой максимума х*. При этом f max= f (x *)=5,4.
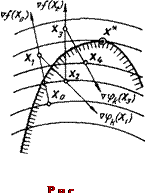 |
Задача с нелинейными ограничениями. Если в задачах с линейными ограничениями движение по граничным прямым оказывается возможным и даже целесообразным, то при нелинейных ограничениях, определяющих выпуклую область, любое как угодно малое перемещение из граничной точки может сразу вывести за пределы области допустимых решений, и возникнет необходимость в возвращении в допустимую область (рис. 7.9). Подобная ситуация характерна для задач, в которых экстремум функции f (x) достигается на границе области. В связи с этим применяются различные
способы перемещения, обеспечивающие построение последовательности точек, расположенных вблизи границы и внутри допустимой области, или зигзагообразное движение вдоль границы с пересечением последней. Как видно из рисунка, возврат из точки x1 в допустимую область следует осуществлять вдоль градиента той граничной функции 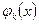 , которая оказалась нарушенной. Это обеспечит отклонение очередной точки х2 в сторону точки экстремума х*. Признаком экстремума в подобном случае будет коллинеарность векторов
, которая оказалась нарушенной. Это обеспечит отклонение очередной точки х2 в сторону точки экстремума х*. Признаком экстремума в подобном случае будет коллинеарность векторов 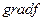 и
и 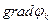 .
.
|
|
|
|
|
Дата добавления: 2014-01-07; Просмотров: 1953; Нарушение авторских прав?; Мы поможем в написании вашей работы!