
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Частные случаи общего уравнения плоскости
|
|
|
|
Лемма о параллельности вектора и плоскости.
Лемма 1 (о параллельности вектора и плоскости). Пусть в аффинной системе координат  дана плоскость
дана плоскость 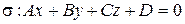 и вектор
и вектор 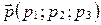 . Для того, чтобы вектор
. Для того, чтобы вектор  был параллелен плоскости
был параллелен плоскости 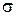 , необходимо и достаточно, чтобы выполнялось условие
, необходимо и достаточно, чтобы выполнялось условие 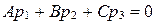 .
.
□ Чтобы доказать необходимость и достаточность этого условия, возьмем точку 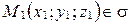 и отложим от нее вектор
и отложим от нее вектор 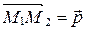 (рис. 68).
(рис. 68).
Пусть  , тогда
, тогда 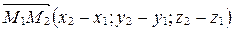 .
.
 Из равенства векторов
Из равенства векторов  и
и  следует равенство их соответственных координат:
следует равенство их соответственных координат:
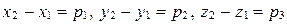 . (24)
. (24)
Так как  , то
, то
 . (25)
. (25)
Если  , то
, то  , следовательно,
, следовательно,
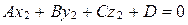 . (26)
. (26)
Вычитаем почленно из уравнения (26) уравнение (25):
 .
.
Применяя формулы (24), получаем:
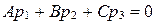 .
.
Обратно, пусть имеет место условие 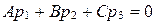 . Тогда из формул (24) следует, что
. Тогда из формул (24) следует, что  .
.
Сложив почленно последнее уравнение с уравнением (25), получим:
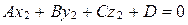 ,
,
откуда следует, что  . Поэтому
. Поэтому 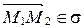 , а так как
, а так как  , то
, то  . ■
. ■
Выясним особенности расположения плоскости 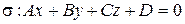 относительно аффинной системы координат, если некоторые из коэффициентов в ее общем уравнении равны 0.
относительно аффинной системы координат, если некоторые из коэффициентов в ее общем уравнении равны 0.
1. 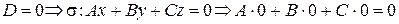 - верное равенство
- верное равенство 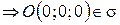 .
.
Обратно, пусть  , тогда
, тогда 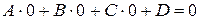 - верное равенство
- верное равенство  .
.
Итак,  .
.
2. 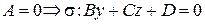 .
.
Возьмем вектор  . Проверим выполнимость условия
. Проверим выполнимость условия 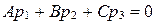 :
:
 ;
;
0=0.
Следовательно, по лемме о параллельности вектора и плоскости  . Поэтому возможны два случая
. Поэтому возможны два случая 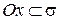 или
или 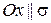 . Учитывая, что
. Учитывая, что  , т.е.
, т.е. 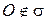 , получаем:
, получаем: 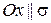 .
.
Обратно, пусть  , тогда
, тогда  . По лемме о параллельности вектора и плоскости
. По лемме о параллельности вектора и плоскости 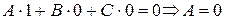 .
.
Итак,  .
.
Рассуждая аналогично, рассмотрите самостоятельно случаи 3 и 4:
3.  .
.
4.  .
.
5. Пусть 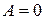 и
и 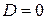 . Тогда из пункта 2 следует, что
. Тогда из пункта 2 следует, что  , т.е.
, т.е. 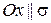 или
или 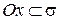 ; а из пункта 1 следует, что
; а из пункта 1 следует, что 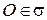 . Значит,
. Значит, 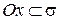 .
.
Обратно, пусть 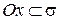 . Тогда
. Тогда 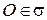 , т.е.
, т.е. 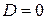 (см. пункт 1). Кроме того,
(см. пункт 1). Кроме того, 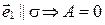 (см. пункт 2).
(см. пункт 2).
Итак, 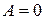 и
и  .
.
В этом случае уравнение плоскости 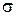 примет вид
примет вид  .
.
Рассуждая аналогично, рассмотрите самостоятельно случаи 6 и 7:
6. 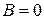 и
и 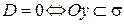 .
.
7.  и
и 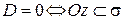 .
.
8. 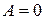 и
и 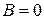 . Тогда из пункта 2 следует, что
. Тогда из пункта 2 следует, что  ; а из пункта 3 следует, что
; а из пункта 3 следует, что . Таким образом,
. Таким образом,
|
|
|
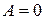 и
и  .
.
В этом случае уравнение 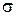 примет вид
примет вид  или
или 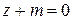 (где
(где  ).
).
Рассуждая аналогично, рассмотрите случаи 9 и 10:
9. 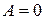 и
и 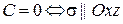 .
.
10. 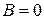 и
и 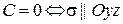 .
.
Из пунктов 8 и 1 получаем случай
11. 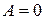 ,
, 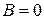 и
и 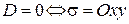 .
.
В этом случае уравнение плоскости будет иметь вид  , т.е.
, т.е.
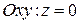 .
.
Из пунктов 9 и 1 получаем случай
12. 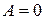 ,
,  и
и  .
.
Тогда уравнение 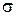 будет иметь вид
будет иметь вид 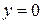 , т.е.
, т.е.
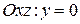 .
.
Из пунктов 10 и 1 получаем случай
13. 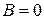 ,
,  и
и  .
.
Уравнение 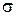 в этом случае имеет вид
в этом случае имеет вид 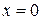 , т.е.
, т.е.
 .
.
Задания для самостоятельной работы
1. Какие из векторов  параллельны плоскости
параллельны плоскости  и почему?
и почему?
2. Справедливы ли утверждения, доказанные в пунктах 1-13, если уравнение плоскости задано в прямоугольной декартовой системе координат и почему?
3. Составьте уравнение плоскости, проходящей через точку 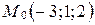 и параллельной плоскости: а)
и параллельной плоскости: а) 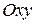 ; б)
; б)  ; в)
; в)  (пользуясь частными случаями общего уравнения плоскости).
(пользуясь частными случаями общего уравнения плоскости).
4. Составьте уравнение плоскости, которая проходит через точку 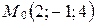 и содержит: а) ось
и содержит: а) ось  ; б) ось
; б) ось 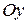 ; в) ось
; в) ось  (пользуясь частными случаями общего уравнения плоскости).
(пользуясь частными случаями общего уравнения плоскости).
§ 23. Основные аффинные задачи,
связанные с плоскостью (обзор)
1. Взаимное расположение двух плоскостей.
Выяснить взаимное расположение двух плоскостей позволяет следующая теорема:
Теорема 1. Пусть в аффинной системе координат  плоскости
плоскости 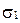 и
и 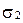 заданы общими уравнениями:
заданы общими уравнениями:
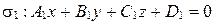 ,
,
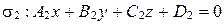 .
.
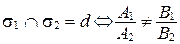 или
или  ;
;
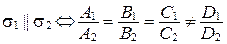 (коэффициенты при х, у, z пропорциональны, а свободные члены им не пропорциональны);
(коэффициенты при х, у, z пропорциональны, а свободные члены им не пропорциональны);
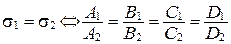 .
.
2. Взаимное расположение трех плоскостей.
Вопрос о взаимном расположении трех плоскостей 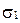 ,
, 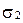 и
и 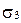 сводится к исследованию вопроса о взаимном расположении трех пар плоскостей:
сводится к исследованию вопроса о взаимном расположении трех пар плоскостей: 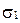 и
и 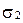 ,
, 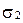 и
и 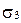 ,
, 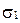 и
и 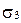 .
.
Возможны восемь случаев взаимного расположения этих плоскостей:
1) 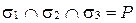 (рис. 69, а);
(рис. 69, а);
2)  (рис. 69, б);
(рис. 69, б);
3)  (рис. 69, в);
(рис. 69, в);
4)  (следовательно,
(следовательно,  ) (рис. 69, г);
) (рис. 69, г);
5) 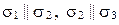 (следовательно,
(следовательно, 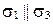 ) (рис. 69, д);
) (рис. 69, д);
6)  (рис. 69, е);
(рис. 69, е);
7) 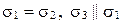 (рис. 69, ж);
(рис. 69, ж);
8) 
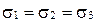 (рис. 69, з).
(рис. 69, з).

3. Геометрический смысл знака многочлена  .
.
Теорема 2. Если в аффинной системе координат плоскость 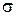 задана уравнением
задана уравнением  , то два полупространства, на которые эта плоскость разбивает пространство, определяются условиями
, то два полупространства, на которые эта плоскость разбивает пространство, определяются условиями
|
|
|
 и
и  .
.
4. Пучок и связка плоскостей.
Пучком плоскостей называется множество всех плоскостей, проходящих через одну и ту же прямую 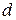 . Прямая
. Прямая 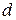 называется осью этого пучка.
называется осью этого пучка.
Пусть  . Тогда уравнение пучка плоскостей с осью
. Тогда уравнение пучка плоскостей с осью 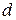 имеет вид:
имеет вид:
 , где
, где 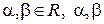 не равны нулю одновременно.
не равны нулю одновременно.
Связкой плоскостей называется множество всех плоскостей, проходящих через одну и ту же точку 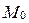 . Точка
. Точка 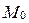 называется центром связки.
называется центром связки.
Пусть  . Тогда уравнение связки плоскостей имеет вид:
. Тогда уравнение связки плоскостей имеет вид:
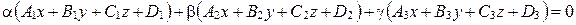 , где
, где 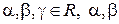 и
и 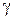 не равны нулю одновременно.
не равны нулю одновременно.
Задания для самостоятельной работы
1. Пользуясь теоремой 1 из § 22, выведите уравнение плоскости, параллельной плоскости  и проходящей через начало координат.
и проходящей через начало координат.
2. Найдите уравнение плоскости, параллельной плоскости  и проходящей через точку
и проходящей через точку 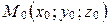 .
.
3. В аффинной системе координат задана плоскость 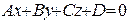 . Какая фигура определяется условием: а)
. Какая фигура определяется условием: а) 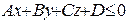 ; б)
; б) 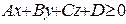 ?
?
4. Верно ли утверждение, что плоскость  пересекает отрезок
пересекает отрезок 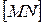 , где
, где  , тогда и только тогда, когда
, тогда и только тогда, когда 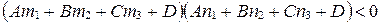 и почему?
и почему?
5. Составьте уравнение плоскости, проходящей через начало координат и содержащей линию пересечения плоскостей 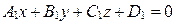 и
и  .
.
|
|
|
|
|
Дата добавления: 2014-01-07; Просмотров: 2199; Нарушение авторских прав?; Мы поможем в написании вашей работы!