
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Кольцо целостности
Пусть 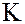 – произвольное кольцо. Как было показано ранее, для любого элемента
– произвольное кольцо. Как было показано ранее, для любого элемента  выполняются равенства:
выполняются равенства:
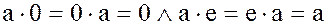 .
.
Отсюда следует, что нулевой – 0 и единичный – 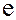 элементы являются различными элементами кольца.
элементы являются различными элементами кольца.
Если для элемента  в кольце
в кольце 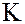 существует обратный элемент
существует обратный элемент 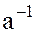 , то он единственный, для которого выполняется условие
, то он единственный, для которого выполняется условие  .
.
Единичный элемент кольца 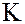 является обратным для самого себя:
является обратным для самого себя: 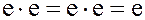 .
.
Из равенства  следует, что элемент
следует, что элемент 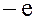 также является обратным для самого себя.
также является обратным для самого себя.
Нулевой элемент 0 кольца 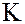 не имеет обратного элемента, поскольку
не имеет обратного элемента, поскольку  , для любого элемента
, для любого элемента  .
.
Определение. Элемент  , для которого в кольце
, для которого в кольце 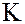 существует, и притом только единственный, обратный элемент
существует, и притом только единственный, обратный элемент 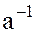 , называют обратимым или делителем единицы.
, называют обратимым или делителем единицы.
Кольцо целых чисел является самым простым примером коммутативного кольца, в котором только 1 и –1 являются делителями единицы 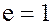 .
.
Теорема. Множество  всех делителей единицы
всех делителей единицы 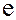 кольца
кольца 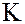 является группой по умножению.
является группой по умножению.
Доказательство. Действительно, если 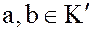 , т.е. являются делителями единицы
, т.е. являются делителями единицы 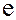 кольца
кольца  , то
, то
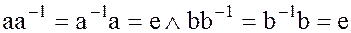
и, следовательно,
 .
.
А это означает, что 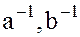 и
и 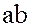 также являются делителями единицы
также являются делителями единицы 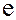 и, следовательно, содержатся в множестве
и, следовательно, содержатся в множестве  . Поэтому множество
. Поэтому множество  является группой по умножению.
является группой по умножению.
Определение. Группа  называется группой делителей единичного элемента
называется группой делителей единичного элемента 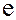 кольца
кольца 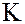 .
.
Так как для любого элемента  выполняется равенство
выполняется равенство 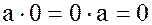 , то по определению делителей элементов кольца, каждый элемент является делителем нуля. В теории колец для произвольных элементов
, то по определению делителей элементов кольца, каждый элемент является делителем нуля. В теории колец для произвольных элементов  используют следующее определение делителей нуля.
используют следующее определение делителей нуля.
Определение. Элементы  называются делителями нуля, если
называются делителями нуля, если 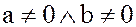 , а
, а 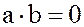 ; при этом
; при этом 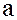 называют левым, а
называют левым, а 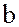 – правым делителем нуля.
– правым делителем нуля.
Пример. 1. В кольце классов вычетов по mod m существуют делители нуля:
в  :
: 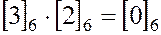 ,
,
в  :
: 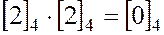 .
.
2. В кольце квадратных матриц второго порядка также существуют делители нуля:
пусть 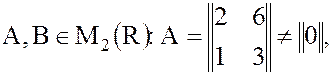
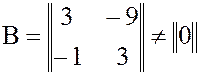 ,
,
тогда  .
.
Определение. Кольцом (областью) целостности называется коммутативное кольцо без делителей нуля.
Пример. 1. 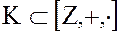 – кольцо целых чисел является кольцом целостности.
– кольцо целых чисел является кольцом целостности.
2. Кольцо  является кольцом целостности в том и только в том случае, если
является кольцом целостности в том и только в том случае, если 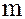 – простое число.
– простое число.
Рассмотрим произвольное кольцо 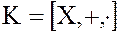 . Если
. Если 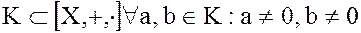 , и
, и 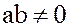 , т.е. кольцо не содержит делителей нуля, то такое кольцо называется телом. Более строго.
, т.е. кольцо не содержит делителей нуля, то такое кольцо называется телом. Более строго.
Определение. Кольцо K, в котором для всех отличных от нуля элементов существуют обратные, называется телом.
Тело не содержит делителей нуля, т.е. если  и
и 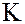 – тело, то, если
– тело, то, если 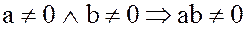 .
.
Это означает, что отличные от нуля элементы тела образуют полугруппу по умножению.
Более того, т.к. тело содержит единичный элемент и для каждого отличного от нуля элемента в теле существует обратный элемент, то элементы тела, отличные от нуля образуют группу по умножению.
Примеры. 1. Тело рациональных чисел  . Действительно, если
. Действительно, если 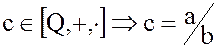 , где
, где 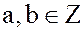 .
.
Если  .
.
Важно, чтобы обратный элемент  .
.
Для любого целого числа, например  , обратный существует и равен
, обратный существует и равен 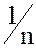 , но он не принадлежит
, но он не принадлежит 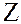 .
.
2. Тело вещественных чисел.
3. Тело комплексных чисел.
Кольцом целостности, с которым наиболее часто приходится встречаться, является кольцо целых чисел 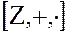 .
.
В теории колец особую роль играют кольца, которые по своим свойствам достаточно близки к кольцу целых чисел. В частности, для этих колец можно развить теорию делимости, аналогичную теории делимости целых чисел. Эти кольца получили название колец главных идеалов. Пусть 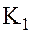 – кольцо целостности с единицей – коммутативное кольцо без делителей нуля, в котором понятие правого и левого делителя элемента совпадают. Определение делимости элементов этого кольца можно сформулировать так:
– кольцо целостности с единицей – коммутативное кольцо без делителей нуля, в котором понятие правого и левого делителя элемента совпадают. Определение делимости элементов этого кольца можно сформулировать так:
Определение. Если для элементов  кольца целостности
кольца целостности 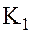 в
в 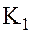 существует такой элемент
существует такой элемент  , что
, что 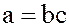 , то говорят, что элемент
, то говорят, что элемент 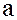 делится на
делится на 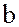 , и пишут
, и пишут  или
или 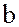 делит
делит 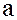 –
– 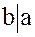 , или
, или  .
.
Из определения делимости двух элементов вытекают следующие свойства делимости в кольце целостности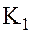 :
:
1. 
2. 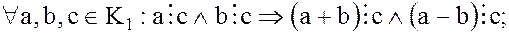
3. 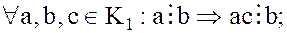
4. 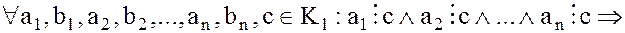
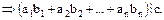
Эти свойства являются распространением на кольцо целостности  соответствующих свойств делимости в кольце целых чисел.
соответствующих свойств делимости в кольце целых чисел.
5. Каждый элемент 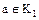 делится на любой делитель
делится на любой делитель  единицы
единицы 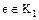 . Действительно, если
. Действительно, если 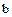 – делитель единицы, то и
– делитель единицы, то и  – также делитель единицы, а это означает, что
– также делитель единицы, а это означает, что 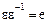 , тогда
, тогда 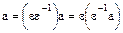 и, следовательно,
и, следовательно,  .
.
6. Если 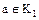 делится на
делится на 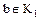 , то
, то  делится и на
делится и на 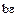 , где
, где  – любой делитель единицы.
– любой делитель единицы.
Действительно, из равенства 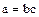 следует равенство
следует равенство 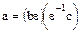 и, следовательно,
и, следовательно, 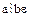 .
.
7. Каждый элемент из делителей  и
и 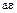 , где
, где  – любой делитель единицы, является делителем и другого.
– любой делитель единицы, является делителем и другого.
Действительно, из равенства 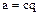 следует равенство
следует равенство  , а из равенства
, а из равенства 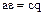 – равенство
– равенство  . Следовательно, если
. Следовательно, если 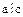 , то
, то 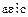 , и наоборот.
, и наоборот.
В дальнейшем будем рассматривать элементы кольца целостности  , отличные от нуля.
, отличные от нуля.
Определение. Элементы  кольца целостности
кольца целостности  называются ассоциированными, если каждый из них является делителем другого:
называются ассоциированными, если каждый из них является делителем другого:
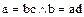 . (55)
. (55)
Из равенства (55) следует, что 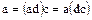 . Отсюда, сократив обе части полученного равенства на
. Отсюда, сократив обе части полученного равенства на 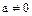 , получаем
, получаем 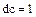 . Следовательно,
. Следовательно, 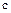 и
и 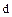 являются делителями единицы. Таким образом, если
являются делителями единицы. Таким образом, если  и
и 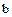 – ассоциированные элементы, то
– ассоциированные элементы, то 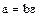 , где
, где  – некоторый делитель единицы. С другой стороны, какой бы мы не взяли делитель единицы
– некоторый делитель единицы. С другой стороны, какой бы мы не взяли делитель единицы 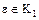 , элементы
, элементы  и
и 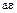 ассоциированные между собой, поскольку
ассоциированные между собой, поскольку 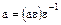 .
.
Определение. Элементы  кольца целостности
кольца целостности  называются ассоциированными, если
называются ассоциированными, если  , где
, где  – некоторый делитель единицы.
– некоторый делитель единицы.
Пример. В кольце целых чисел  ассоциированными являются пары чисел
ассоциированными являются пары чисел 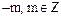 .
.
Если  и
и 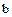 ассоциированные элементы кольца целостности
ассоциированные элементы кольца целостности , то
, то 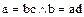 . Отсюда следует, что
. Отсюда следует, что  – главный идеал, порожденный элементом
– главный идеал, порожденный элементом  является подмножеством
является подмножеством  – главного идеала, порожденного элементом
– главного идеала, порожденного элементом 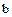 и наоборот:
и наоборот:

Это означает, что два ассоциированных элемента  , кольца целостности
, кольца целостности  порождают один и тот же главный идеал.
порождают один и тот же главный идеал.
Пусть  – произвольные элементы кольца целостности
– произвольные элементы кольца целостности  .
.
Определение. Элемент  называется общим делителем элементов
называется общим делителем элементов  и
и 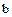 , если каждый из этих элементов делится на
, если каждый из этих элементов делится на 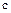 .
.
По свойству 5 все делители единицы 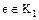 кольца целостности
кольца целостности  являются общими делителями элементов
являются общими делителями элементов  и
и 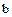 . Но у элементов
. Но у элементов  и
и 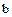 могут быть и другие общие делители. Введем понятие наибольшего общего делителя (НОД) этих элементов. Определение НОД двух целых чисел, по которому НОД называют наибольший из общих делителей, распространить на кольцо целостности нельзя, т.к. в произвольном кольце целостности
могут быть и другие общие делители. Введем понятие наибольшего общего делителя (НОД) этих элементов. Определение НОД двух целых чисел, по которому НОД называют наибольший из общих делителей, распространить на кольцо целостности нельзя, т.к. в произвольном кольце целостности 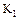 нет отношения порядка. Однако можно ввести и другое определение НОД двух чисел
нет отношения порядка. Однако можно ввести и другое определение НОД двух чисел  и
и 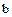 , а именно: НОД двух чисел
, а именно: НОД двух чисел  и
и 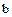 называется такой общий делитель этих чисел, который делится на любой другой их общий делитель. Именно это определение НОД и распространяется на элементы кольца целостности
называется такой общий делитель этих чисел, который делится на любой другой их общий делитель. Именно это определение НОД и распространяется на элементы кольца целостности  .
.
Определение. Наибольшим общим делителем двух элементов  кольца целостности
кольца целостности  называется такой элемент
называется такой элемент 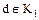 , обозначаемый символом
, обозначаемый символом 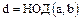 и обладающий двумя свойствами:
и обладающий двумя свойствами:
1. 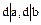 ;
;
2.  .
.
Замечание. Ясно, что вместе с 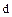 свойствами 1., 2. Обладает любой ассоциированный с ним элемент. Действительно, если
свойствами 1., 2. Обладает любой ассоциированный с ним элемент. Действительно, если 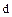 – НОД элементов
– НОД элементов  , то формально это записывается в виде
, то формально это записывается в виде 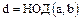 или
или 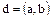 . Если также и
. Если также и 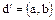 , то элементы
, то элементы 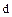 и
и 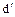 делятся друг на друга и, следовательно, являются ассоциированными. С другой стороны, если
делятся друг на друга и, следовательно, являются ассоциированными. С другой стороны, если 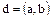 , то, очевидно,
, то, очевидно, 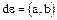 , где
, где  – любой делитель единицы. Таким образом НОД элементов
– любой делитель единицы. Таким образом НОД элементов  определяется с точностью до сомножителя
определяется с точностью до сомножителя  , который является делителем единицы.
, который является делителем единицы.
С учетом этого замечания к свойствам 1., 2. Наибольшего общего делителя добавляются следующие:
3.  ;
;
4.  ;
;
5. 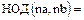
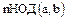 ;
;
6. 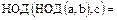
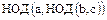 .
.
Свойство 6. позволяет распространить понятие НОД на произвольное конечное число элементов кольца целостности  .
.
По аналогии с  вводится дуальное понятие наименьшего общего кратного
вводится дуальное понятие наименьшего общего кратного  элементов
элементов  кольца целостности
кольца целостности  определенного с точностью до ассоциированности и обладающее также двумя свойствами:
определенного с точностью до ассоциированности и обладающее также двумя свойствами:
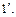
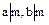 ;
;

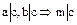 .
.
В частности, полагая 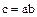 , получаем, что
, получаем, что 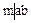 .
.
Теорема. Если для элементов  кольца целостности
кольца целостности  существуют
существуют  и
и  . Тогда
. Тогда
а)  ;
;
б) 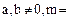
 ,
, 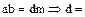
 .
.
Доказательство. Утверждение а) вытекает непосредственно из определения  . Для доказательства б) необходимо убедиться, что элемент
. Для доказательства б) необходимо убедиться, что элемент 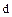 , определенный равенством
, определенный равенством  , обладает свойствами 1., 2. НОД. Действительно, из
, обладает свойствами 1., 2. НОД. Действительно, из  , следовательно
, следовательно 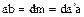 , откуда после сокращения на
, откуда после сокращения на  , допустимого в любом кольце целостности
, допустимого в любом кольце целостности  , имеем
, имеем 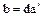 , т.е.
, т.е. 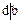 . Аналогично
. Аналогично 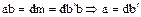 , т.е.
, т.е. 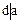 . Этим доказано свойство 1. Для доказательства свойства 2. Представим
. Этим доказано свойство 1. Для доказательства свойства 2. Представим 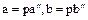 . Положим
. Положим 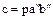 . Тогда
. Тогда 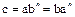 – общее кратное элементов
– общее кратное элементов  и
и 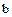 . Согласно свойству
. Согласно свойству 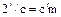 для некоторого
для некоторого  , откуда
, откуда 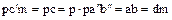 , т.е.
, т.е. 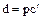 и
и  , что и требовалось доказать.
, что и требовалось доказать.
Определение. Элементы  кольца целостности
кольца целостности  называются взаимно простыми, если они не имеют общих делителей, отличных от делителей единицы, т.е. если НОД
называются взаимно простыми, если они не имеют общих делителей, отличных от делителей единицы, т.е. если НОД .
.
Пусть  – произвольный делитель единицы, и
– произвольный делитель единицы, и 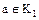 – произвольный элемент кольца целостности
– произвольный элемент кольца целостности  . Тогда из условия
. Тогда из условия 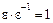 следует, что
следует, что 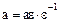 . Это означает, что все элементы ассоциированные с элементом
. Это означает, что все элементы ассоциированные с элементом  , и все делители единицы являются делителями элемента
, и все делители единицы являются делителями элемента 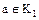 . Их называют тривиальными или несобственными делителями элемента
. Их называют тривиальными или несобственными делителями элемента  . Все делители отличные от
. Все делители отличные от 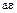 и
и  , если такие существуют в
, если такие существуют в  , называются нетривиальными, или собственными делителями элемента
, называются нетривиальными, или собственными делителями элемента 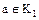 .
.
Пример. В кольце целых чисел  тривиальными делителями числа 10 являются числа
тривиальными делителями числа 10 являются числа 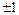 и
и 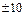 , а нетривиальными – числа
, а нетривиальными – числа  и
и  .
.
Определение. Элемент 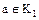 кольца целостности
кольца целостности  называется неразложимым, или простым, если он не является делителем единицы и не имеет нетривиальных делителей; элемент
называется неразложимым, или простым, если он не является делителем единицы и не имеет нетривиальных делителей; элемент 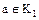 называется разложимым, или составным, если он имеет нетривиальные делители.
называется разложимым, или составным, если он имеет нетривиальные делители.
Другими словами, элемент 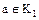 называется разложимым, если его можно представить в виде произведения
называется разложимым, если его можно представить в виде произведения 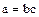 двух нетривиальных делителей
двух нетривиальных делителей 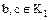 ; элемент
; элемент 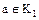 – называется неразложимым, если его нельзя представить в виде произведения двух нетривиальных делителей.
– называется неразложимым, если его нельзя представить в виде произведения двух нетривиальных делителей.
Пример. В кольце целых чисел  неразложимыми являются числа
неразложимыми являются числа 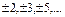 т.е. простые числа и противоположные простым. Все остальные числа отличные от
т.е. простые числа и противоположные простым. Все остальные числа отличные от 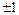 , – разложимы.
, – разложимы.
Неразложимые элементы обладают следующими свойствами:
· если элемент 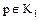 кольца целостности
кольца целостности  неразложимый, то и любой ассоциированный с ним элемент
неразложимый, то и любой ассоциированный с ним элемент  также неразложимый;
также неразложимый;
· если 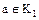 – произвольный элемент кольца целостности
– произвольный элемент кольца целостности  , а
, а 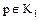 – неразложимый элемент из
– неразложимый элемент из  , то или
, то или  делится на
делится на 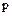 , или
, или  и
и 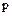 – взаимно простые элементы из
– взаимно простые элементы из  .
.
Действительно, первое свойство следует непосредственно из свойства 7 делимости элементов кольца целостности. Второе свойство докажем следующим образом. Если НОД , то
, то 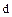 как делитель неразложимого элемента
как делитель неразложимого элемента 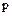 , является либо некоторым делителем единицы
, является либо некоторым делителем единицы  , либо элементом вида
, либо элементом вида 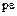 . В первом случае элементы
. В первом случае элементы  и
и 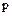 взаимно простые, во втором –
взаимно простые, во втором –  делится на
делится на 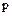 .
.
Определение. Кольцо целостности  называется кольцом с однозначным разложением на простые множители (или факториальным кольцом), если любой элемент
называется кольцом с однозначным разложением на простые множители (или факториальным кольцом), если любой элемент 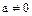 из
из  можно представить в виде:
можно представить в виде:
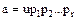 , (46)
, (46)
где  обратный элемент, а
обратный элемент, а 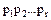 – простые элементы (не обязательно попарно различные), причем из существования другого такого разложения
– простые элементы (не обязательно попарно различные), причем из существования другого такого разложения
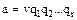
следует, что 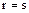 и при надлежащей нумерации элементов
и при надлежащей нумерации элементов 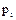 и
и  будет
будет
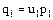 ,
,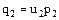 ,…,
,…,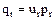 ,
,
где  – обратные элементы в
– обратные элементы в  . Допуская в разложении (46)
. Допуская в разложении (46) 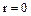 , мы принимаем соглашение, что обратимые элементы
, мы принимаем соглашение, что обратимые элементы  в кольце целостности
в кольце целостности  также имеют разложение на простые множители. Ясно, что если
также имеют разложение на простые множители. Ясно, что если 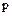 – простой, а
– простой, а  обратный элемент в
обратный элемент в  , то ассоциированный с
, то ассоциированный с 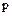 элемент
элемент 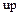 тоже простой.
тоже простой.
Пример. В кольце целых чисел  с обратимыми элементами
с обратимыми элементами  и
и 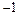 отношение порядка
отношение порядка 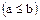 дает возможность выделить положительное простое число
дает возможность выделить положительное простое число 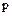 из двух возможных простых элементов
из двух возможных простых элементов 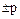 .
.
Теорема. Пусть  – произвольное кольцо целостности с разложением на простые множители. Однозначность разложения в
– произвольное кольцо целостности с разложением на простые множители. Однозначность разложения в  (факториальность
(факториальность  ) имеет место тогда и только тогда, когда любой простой элемент
) имеет место тогда и только тогда, когда любой простой элемент 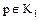 , делящий произведение
, делящий произведение 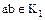 , делит по крайней мере один из сомножителей
, делит по крайней мере один из сомножителей  или
или 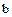 .
.
Доказательство. Пусть  . Если
. Если
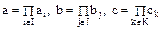
разложения 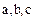 на простые множители, а
на простые множители, а  – кольцо с однозначным разложением, то из равенств
– кольцо с однозначным разложением, то из равенств  следует, что элемент
следует, что элемент 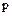 ассоциирован с одним из
ассоциирован с одним из 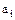 или
или 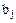 , т.е.
, т.е. 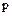 делит
делит  или
или 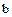 .
.
Обратно, установим однозначность разложения в  , где
, где 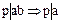 или
или 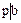 . Рассуждая по индукции, допустим, что разложение всех элементов из
. Рассуждая по индукции, допустим, что разложение всех элементов из  с числом
с числом 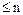 простых множителей единственно (с точностью до порядка сомножителей и их ассоциированности).
простых множителей единственно (с точностью до порядка сомножителей и их ассоциированности).
Докажем теперь это для любого элемента 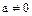 , который может быть разложен на
, который может быть разложен на  простых сомножителей. Именно, пусть
простых сомножителей. Именно, пусть
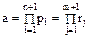 (47)
(47)
– два разложения элемента  с
с 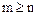 .
.
Условие теоремы, примененное к 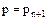 дает нам, что
дает нам, что 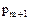 должен делить один из элементов
должен делить один из элементов 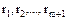 . Без ограничения общности (это вопрос нумерации) будем считать, что
. Без ограничения общности (это вопрос нумерации) будем считать, что 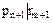 . Но
. Но 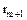 – простой элемент, поэтому
– простой элемент, поэтому  , где
, где  – обратимый элемент. Используя закон сокращения в
– обратимый элемент. Используя закон сокращения в  , получаем из (41) равенство
, получаем из (41) равенство
 . (48)
. (48)
В левой части равенства (42) стоит произведение 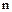 простых сомножителей. По предположению индукции
простых сомножителей. По предположению индукции  и оба разложения отличаются лишь порядком простых элементов, снабженных, возможно, какими–то обратимыми сомножителями.
и оба разложения отличаются лишь порядком простых элементов, снабженных, возможно, какими–то обратимыми сомножителями.
Замечание. В произвольном кольце целостности  элемент
элемент 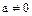 вообще не обязан допускать разложение типа (40). Более интересным является тот факт, что имеются кольца целостности, в которых разложение на простые множители хотя и возможно, но не является однозначным, т.е. условия теоремы, кажущиеся тривиальными не всегда выполняются.
вообще не обязан допускать разложение типа (40). Более интересным является тот факт, что имеются кольца целостности, в которых разложение на простые множители хотя и возможно, но не является однозначным, т.е. условия теоремы, кажущиеся тривиальными не всегда выполняются.
Пример. Рассмотрим кольцо целостности 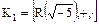 , где
, где 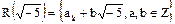 .
.
Норма 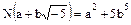 каждого отличного от нуля элемента
каждого отличного от нуля элемента  – целое положительное число. Если элемент
– целое положительное число. Если элемент  обратим в
обратим в  , то
, то 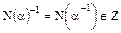 , откуда
, откуда  . Это возможно лишь при
. Это возможно лишь при 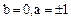 . Таким образом в
. Таким образом в  , как и в 1
, как и в 1 , обратимыми элементами являются только
, обратимыми элементами являются только 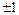 . Если
. Если 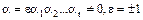 , то
, то 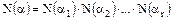 . Так как
. Так как 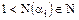 , то при заданном
, то при заданном 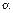 число множителей
число множителей 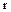 не может неограниченно расти. Следовательно, разложение на простые множители в
не может неограниченно расти. Следовательно, разложение на простые множители в  возможно. Вместе с тем число 9 (да и не только оно) допускает два существенно различных разложения на простые множители:
возможно. Вместе с тем число 9 (да и не только оно) допускает два существенно различных разложения на простые множители:
 .
.
Неассоциированность элементов 3 и 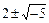 очевидна. Далее,
очевидна. Далее, 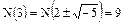 . Поэтому из разложения
. Поэтому из разложения 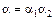 для
для 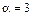 или
или 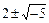 с необратимыми
с необратимыми 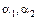 следовало бы
следовало бы  , т.е.
, т.е.  , что невозможно, поскольку уравнение
, что невозможно, поскольку уравнение 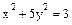 с
с 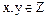 неразрешимо. Этим доказана простота элементов 3 и
неразрешимо. Этим доказана простота элементов 3 и 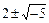 .
.
|
Дата добавления: 2014-01-07; Просмотров: 1879; Нарушение авторских прав?; Мы поможем в написании вашей работы!