Линейное неоднородное ДУ второго порядка с постоянными коэффициентами имеет вид

(**)

где - постоянные числа, - известная функция от .

Теорема. Общее решение неоднородного уравнения (**) равно сумме общего решения соответствующего однородного уравнения (*) и частного решения данного неоднородного уравнения.

Так как находить общее решение линейного однородного ДУ с постоянными коэффициентами мы умеем, то осталось указать способ нахождения частного решения данного неоднородного линейного ДУ. При рассмотрении этой задачи мы ограничимся лишь простейшими правыми частями уравнения

.

1) Правая часть уравнения есть показательная функция, т.е.

.

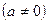a) Если 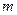не является корнем характеристического уравнения, то частное решение ищем в виде .

b) Если характеристическое уравнение имеет два равных корня и 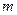- один из корней, то частное решение ищем в виде .

c) Если характеристическое уравнение имеет два одинаковых корня, равных числу 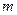, то частное решение ищут в виде .

Пример. Решить уравнение .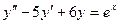

Решение. Решаем соответствующее однородное уравнение .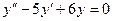

Характеристическое уравнение имеет корни . Общее решение однородного уравнения .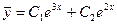

Так как не является корнем характеристического уравнения, то частное решение ищем в виде 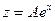, где - неопределённый коэффициент. Тогда , и, подставляя в уравнение, имеем , откуда 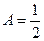. Итак, частное решение 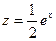. Общее решение линейного неоднородного уравнения

.

2) Правая часть неоднородного уравнения есть тригонометрический полином

.

Частное решение ищут в форме тригонометрического полинома , где и неопределённые коэффициенты, или .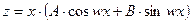

Пример. Решить уравнение .

Решение. Соответствующее однородное уравнение имеет два одинаковых корня 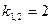. Следовательно, общее решение его .

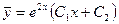Будем искать частное решение в виде . Тогда 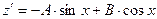, . Подставляя в уравнение и приравнивая коэффициенты при и 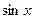справа и слева, получим

откуда 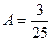, 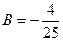. Частное решение .

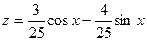Общее решение данного неоднородного уравнения .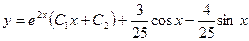

3) Правая часть линейного уравнения представляет собой многочлен, например, второй степени

.

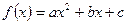
Ищем частное решение этого уравнения в виде

,

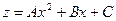где 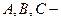неопределённые коэффициенты, если 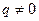. Если же 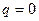, то при 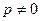частное решение ищем в виде .

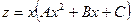Аналогично поступают, если многочлен другой степени.

Пример. Решить уравнение .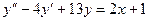

Решение. Составим характеристическое уравнение соответствующего однородного уравнения

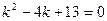
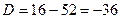
Общее решение .

Частное решение ищем в виде .

Отсюда , . Подставляя в неоднородное уравнение, получим , . Частное решение .

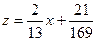Общее решение неоднородного уравнения .

Литература:

1. Письменный Д.Т. Конспект лекций по высшей математике 1 и 2 ч.: - М.: Айрис-пресс, 2004. – 280с.

2. Кремер Н.Ш. Высшая математика для экономистов. М.: «Юнити». 1997г.

3. Минорский В.П. Сборник задач по высшей математике.: М., 1978.- 352с.

4. Яблонский А.И. Высшая математика.: Мн.: Высшая школа. 1993.

5. Гусак А.А. Задачи и упражнения по высшей математике.: Мн.: Высшая школа. 1988.

6. Гурский Е.И. Руководство к решению задач по высшей математике.: Мн.: Высшая школа. 1989.

7. Александров П.С. Курс аналитической геометрии и линейной алгебры. – М: Наука, 1979.

8. Бурдун А.А., Мурашко Е.А., Толкачёв М.М., Феденко А.О. Сборник задач по алгебре и аналитической геометрии. – Мн.: Университетское, 1989.

9. Милованов М.В., Тышкевич Р.И., Феденко А.С. Алгебра и аналитическая геометрия. Часть I, II. – Мн.: Вышэйшая школа, 1984, 1987.

Учебное издание

БУЗЛАНОВ АЛЕКСАНДР ВАСИЛЬЕВИЧ

БОРОДИЧ РУСЛАН ВИКТОРОВИЧ

БОРОДИЧ ТИМУР ВИКТОРОВИЧ

БОРОДИЧ ЕЛЕНА НИКОЛАЕВНА

Дата добавления: 2014-01-07