
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Площадь фигуры, ее основные свойства. Способы измерения площадей фигур. Единицы площади
|
|
|
|
Цель изучения темы: введение понятий площади плоской фигуры, равновеликости и равносоставленности фигур, обобщение и систематизация имеющихся знаний о единицах площади и измерении площадей простейших фигур.
План:
1. Площадь фигуры.
2. Способы измерения площади фигуры.
3. Равновеликие и равносоставленные фигуры.
4. Единицы площади. Отношения между ними.
5. Измерение площадей простейших фигур.
6. Измерение площадей фигур в начальной школе.
Рассмотрим вопрос о площади плоской фигуры и способах измерения площадей.
Дадим аксиоматическое определение площади, согласно [4] и аксиоматическим определениям темы 1.
Функцией площади называется любая функция S: U ® R>0, обладающая свойствами:
1) конечной аддитивности, т.е. " u, v Є u,
S (u + v) = S(u) + S(v);
2) Gs — инвариантности, т.е. "u Є U, " g Є (L2 х R2),
S(u) = S (fg(u)).
Рассмотрим основы теории измерения площадей плоских фигур, взяв за основу подход, впервые изложенный французским математиком К. Жорданом согласно[2].
Пусть М — множество фигур на плоскости, имеющих замкнутых контур, и Ф — одна из таких фигур, площадь которой надо измерить. По отношению к фигуре Ф будем различать внутренние и внешние точки, а так же точки контура. Далее, через производную точку плоскости проведем две взаимно перпендикулярные прямые (оси) и выберем единичный отрезок l. Откладывая на каждой прямой единичный отрезки, равные единичному, и проведя через их концы прямые, параллельные осям, получим на плоскости сеть квадратов (рис. 1), площадь каждого из которых равна единице.
Заштрихуем те квадраты, через которые проходит контур фигуры Ф. Тогда по отношению к фигуре Ф выделяются квадраты трех видов:
|
|
|
1) квадраты, целиком состоящие из внутренних точек фигуры Ф;
2) квадраты, состоящие как из внутренних, так и внешних точек фигуры (на рис. 1 они заштрихованы);
3) квадраты, не содержащие внутренних точек фигуры Ф.
 Система квадратов, являющаяся объединением квадратов первого и второго видов, называется покрывающей системой квадратов по отношению к фигуре Ф.
Система квадратов, являющаяся объединением квадратов первого и второго видов, называется покрывающей системой квадратов по отношению к фигуре Ф.
Система квадратов, состоящая из всех квадратов первого вида, называется внутренней системой квадратов по отношению к фигуре Ф.
Численные значения площадей внутренней и покрывающей систем квадратов легко подсчитать. Если рассматривать только единичные квадраты, то эти значения выражаются натуральными числами m1 и n1 соответственно. Здесь m1 — число единичных квадратов, целиком лежащих внутри фигуры Ф, а n1 — число единичных квадратов покрывающей системы для фигуры Ф. Таким образом, m1 и n1 будут приближенными значениями измеряемой площади: первое m1 — с недостатком; второе n1 — с избытком.
Разделим каждую из сторон единичного квадрата на 10 равных частей и проведем через точки деления прямые, параллельные сторонам квадрата. При этом единичный квадрат разложится на 100 равных квадратов. Пользуясь новым квадратом, образуем на плоскости более мелкую сеть. Обозначим через m2 и n2 число новых квадратов внутренней и покрывающей систем, соответственно. Тогда числа  будут новыми приближениями к численному значению площади фигуры Ф, причем с большей точностью.
будут новыми приближениями к численному значению площади фигуры Ф, причем с большей точностью.
Деля каждую из сторон малых квадратов снова на 10 равных частей, образуем еще более мелкую сеть. При этом числа 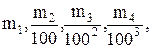 … образуют последовательность приближений к численному значению площади фигуры Ф по недостатку, а числа
… образуют последовательность приближений к численному значению площади фигуры Ф по недостатку, а числа  … — последовательность приближений по избытку. Очевидно, что последовательность
… — последовательность приближений по избытку. Очевидно, что последовательность 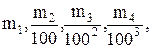 … является неубывающей, т.е.
… является неубывающей, т.е.  …, а последовательность
…, а последовательность  … — невозрастающей, т.е.
… — невозрастающей, т.е.  …
…
Кроме того, для любого j > 1 имеем: 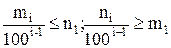
Из соотношения 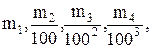 и
и 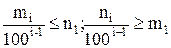 вытекает существование пределов этих последовательностей:
вытекает существование пределов этих последовательностей:
|
|
|
 и
и 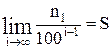 .
.
Число s называют значением внутренней площади фигуры Ф, а число S — значением внешней площади. Очевидно, что s £ S, т.к. при любом номере i имеет место неравенство mi £ ni.
|
В ходе описанных рассуждений мы построили отображение
множества квадрируемых фигур М во множество положительных действительных чисел R+.
Рассмотрим основные свойства указанного отображения.
1. (Существование единицы площади) Значение площади единичного квадрата Е = l2 равно единице, т.е. S(E) = 1.
2. (Свойство инвариантности площади) Площадь равных фигур при выбранной единице измерения выражаются одним и тем же числом: ("Ф1,Ф2 Є М) (Ф1 = Ф2 => SE(Ф1) = SE(Ф2)). Справедливость этого утверждения следует из определения равенства геометрических фигур. Равными в геометрии считаются любые фигуры, которые при движении могут быть совмещены. В этих условиях внутренняя и покрывающая системы квадратов фигуры Ф2 ничем не отличаются от внутренней и покрывающей системы квадратов фигуры Ф1, а значит и значения площадей для них выражаются одним и тем же числом.
3. (Свойство аддитивности площади) Если фигура составлена из конечного числа квадрируемых фигур, то она квадрируема, и значение ее плошади ровно сумме значений площадей составляющих фигур ("Ф Є М)
(Ф = Ф1 È Ф2 È … È Фn => SE(Ф) = SE(Ф1) + SE(Ф2) + … + SE(Фn). Говоря, что фигура Ф составлена из фигур Ф1, Ф2, … Фn, имеем в виду, что она является их объединением, и любые две данные фигуры не имеют общих внутренних точек.
4. (Свойство монотонности площади) Если квадрируемая фигура Ф1, лежит внутри квадрируемой фигуры Ф2, то значение площади SE(Ф1) меньше значения SE(Ф2): ("Ф1Ф2 Є М) (Ф1 < Ф2 => SE(Ф1) < SE(Ф2)).
Для доказательства этого свойства обратимся к рисунку №3.
Фигура Ф2/Ф1, заключенная между границами квадрируемых фигур, будет квадрируемой,а значит к фигуре Ф2 применимо свойство аддитивности, согласно которому S(Ф2)=S(Ф1) + S(Ф2 Ф1).
Поскольку S(Ф2 Ф1) есть число положительное, то можем заключить, что S(Ф2) < (Ф1).
|
|
|
Фигуры Ф1 и Ф2 называются, равновеликими, если их площади равны.
Фигуры F и Ф называются равносоставленными существуют фигуры F1, F2, …, Fn и Ф1, Ф2, … Фn такие, что выполняются условия:
1) F = F1 È F2 È … È Fn и Ф1 È Ф2 È … È Фn;
2) F1 = Ф1, F2 = Ф2, …, Fn = Фn;
3) фигуры F1, F2, …, Fn и Ф1, Ф2, … Фn фигуры не имеют попарно общих внутренних точек.
Из рассмотренных свойств площади следует, что равносоставленные плоские фигуры всегда равновелики. Обратное, вообще говоря, неверно, но венгерским математиком Ф. Бойяи и немецким любителем математики П. Гервином была доказана теорема: любые два равновеликих многоугольника равносоставлены.
Понятие равносоставленности плоских фигур широко используется в школьном курсе геометрии при выводе формул для вычисления площадей простейших фигур.
Описание выше способ измерения площадей основан на прямом подсчете числа квадратов. Он так и называется прямым. Если сетка квадратов нанесена на прозрачный материал, то такое приспособление называется палеткой.
В начальном курсе математике находят приближенное значение площади фигуры Ф с помощью палетки. Для этого складывают численные значения площади по недостатку и по избытку, а затем делят эту сумму пополам:  .
.
Здесь m — число единичных квадратов внутренней системы, n — число единичных квадратов покрывающей системы, k — число единичных квадратов, через которые проходит контур фигуры Ф. Итак,  .
.
Подобный способ измерения площадей можно применить к прямоугольнику СДЕF со сторонами СД и ДЕ, параллельными осям Ох и Оу (рис. 2).
 Принимая отрезок l за единицу, обозначим длины отрезков CD и DE через a и b, соответственно, а числовые значения длин через ml(a) и ml(b). Линии сетки квадратов образуют на CD и DЕ шкалу отрезков. Прямоугольник СDEF есть квадрируемая фигура, и значит его площадь S, выраженная в единицах
Принимая отрезок l за единицу, обозначим длины отрезков CD и DE через a и b, соответственно, а числовые значения длин через ml(a) и ml(b). Линии сетки квадратов образуют на CD и DЕ шкалу отрезков. Прямоугольник СDEF есть квадрируемая фигура, и значит его площадь S, выраженная в единицах
E = l2, равна произведению
ml(a)·ml(b), т.е. другими словами, число, выражающее площадь прямоугольника в квадратных единицах l2, равно произведению чисел, выражающих длины его сторон в соответствующих линейных единицах.
|
|
|
Единица площади — квадратный метр. Он равен площади квадрата со сторонами, длины которых равны 1 м, обозначается м2.
Аналогично определяется: квадратный километр — км2, квадратный дециметр — дм2, квадратный сантиметр — см2, квадратный миллиметр — мм2.
Основной мерой площади в старину на Руси была десятина — площадь квадрата со стороной в 50 саженей (или 0,1 версты).
Обобщим школьные знания о вычислении площадей некоторых простых плоских фигур в следующей таблице.
| Площади некоторых плоских фигур | |
| Треугольник |  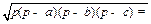 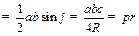 , где a, b, c – стороны треугольника, , где a, b, c – стороны треугольника,
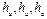 - высоты, p- полупериметр, R – радиус окружности, описанной около треугольника, r – радиус окружности, вписанной в треугольник, - высоты, p- полупериметр, R – радиус окружности, описанной около треугольника, r – радиус окружности, вписанной в треугольник,  – угол, лежащий между сторонами a и b. – угол, лежащий между сторонами a и b.
|
| Параллелограмм | Указание: для вычисления площади параллелограмма удвоить любую из формул, приведенных в правой верхней ячейке таблицы, достроив данный треугольник до параллелограмма.
Пример:  (1), где a и b – стороны параллелограмма, (1), где a и b – стороны параллелограмма,  – угол, лежащий между сторонами a и b.
В качестве дополнения приведем следующую формулу: – угол, лежащий между сторонами a и b.
В качестве дополнения приведем следующую формулу:
 φ (2), где φ (2), где 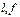 - диагонали параллелограмма, φ – угол между диагоналями. - диагонали параллелограмма, φ – угол между диагоналями.
|
| Ромб | Указание: подставьте в формулу вычисления площади параллелограмма (1)  в формулу вычисления площади параллелограмма (2) значение sin φ при φ= 90° в формулу вычисления площади параллелограмма (2) значение sin φ при φ= 90°
|
| Прямоугольник | Указание: подставьте в формулу вычисления площади параллелограмма (1) значение sin  при при  = 90°; в формулу вычисления площади параллелограмма (2) = 90°; в формулу вычисления площади параллелограмма (2)  . .
|
| Квадрат | Указание: воспользуйтесь формулами вычисления площади прямоугольника и положите  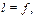 φ = 90°.
φ = 90°.
|
| Трапеция | 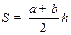 , где a и b – основания трапеции, , где a и b – основания трапеции,  - высота. - высота.
|
| Круг | S = π r ², где r – радиус круга. |
| Площадь правильного n- угольника |  , где , где 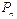 - периметр правильного n-угольника, r – радиус вписанной окружности - периметр правильного n-угольника, r – радиус вписанной окружности
|
Представления о площади фигуры на интуитивном уровне формируются у учащихся в начальном курсе математики. В дальнейшем это понятие развивается и используется в геометрии, где изучаются приемы измерения площадей простейших фигур.
Рассмотрим методику работы над площадью фигуры в начальных классах.
Прежде всего площадь выделяется как свойство плоских предметов среди других их свойств. Дети сравнивают предметы по площади. При этом ученики пользуются наложением предметов или сравнивают их на глаз. В процессе изучения геометрического материала в I-II классах у детей уточняются представления о площади. Более четким становится понимание того, что фигуры могут быть различными и одинаковыми по площади. Дети многократно наблюдают соотношение между всей фигурой и ее частями, упражняются в составлении различных по форме фигур из одних и тех же заданных частей.
Учащиеся знакомятся с единицами площади и упражняются в нахождении площади фигур.
Для нахождения площади геометрических фигур, не разделенных на квадратные сантиметры, используют самостоятельно изготовленную палетку - прозрачную пластинку, разбитую на равные квадраты. Сетка может быть нанесена на кальку или состоять из нитей, натянутых на рамку. Можно изготовить палетку с детьми на уроке труда. Наложив палетку на геометрическую фигуру, подсчитывают число целых и нецелых квадратных сантиметров, которые в ней содержатся.
В то же время приступают к сопоставлению площади и периметра многоугольника.
Далее учащиеся знакомятся с приемом вычисления площади прямоугольника (квадрата) и в уроки включаются устные и письменные задания на вычисление площади прямоугольников (квадратов) и периметров этих фигур
Наряду с решением задач на нахождение площади прямоугольника по данным длине и ширине решают обратные задачи на нахождение одной из сторон по известной площади и другой стороне прямоугольника.
Тема 4.
|
|
|
|
|
Дата добавления: 2014-01-14; Просмотров: 6357; Нарушение авторских прав?; Мы поможем в написании вашей работы!