Непрерывная случайная величина. Плотность распределения

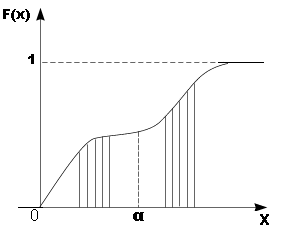
Разобьем непрерывную прямую на n прямоугольников è получаем дискретную функцию распределения è теперь устремим число n к бесконечности è переходим к непрерывной кривой è получаем P{x=a} = 0

Опр. Непрерывной с.в. Х называется с.в., чья функция распределения непрерывна и дифференцируема.

Опр. Средней плотностью распределения на отрезке кривой функции распределения называется отношение вероятности попадания точки на этот отрезок к длине отрезка.

Опр. Плотностью распределения в точке a называется предел плотности на отрезке, содержащего точку a, при стремлении обоих концов отрезка к точке a, т.е. производная функции распределения в этой точке:

Опр. Кривой распределения называется график плотности распределения f(x).

Опр. Рассматриваем непрерывную с.в. Х с плотностью f(x) и элементарный участок dx, примыкающий к точке х.

Опр. Вероятность попадания с.в. Х на этот участок dx равна f(x)dx. Эта величина f(x)dx называется элементом вероятности для точки х.

Теперь вероятность попадания с.в. Х на участок от a до b равна сумме элементов вероятности на всём этом участке, т.е.:

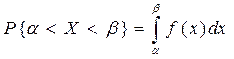
Если за один из концов отрезка мы возьмём - ¥, то можем выразить функцию распределения:

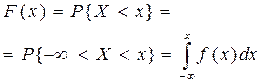
Основные свойства плотности распределения f(x):

1. Плотность распределения неотрицательная функция: f(x) ³ 0

2. Интеграл в бесконечных пределах от плотности распределения равен единице:

Доказательство:

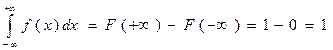
Основные геометрические свойства интерпретируются так:

1. Вся кривая распределения лежит не ниже оси абсцисс.

2. Полная площадь, ограниченная кривой распределения и осью абсцисс, равна единице.

Вывод формулы полной вероятности и формулы Бейеса:

Пусть вероятность события А зависит от значения х с.в. Х с плотностью f(x).

Сделаем гипотезу, состоящую в том, что с.в. Х приняла значения, лежащие на элементарном участке dx, примыкающем к точке х.

В пределе Х=х

Обозначим - условная вероятность события А при Х=х

Интегральная формула полной вероятности:

Формула Бейеса:

Пусть до опыта с.в. Х имела плотность распределения f(x).

Произведён опыт, в результате которого появилось событие А.

Условная вероятность события А при Х=х обозначается .

Интегральная формула Бейеса:

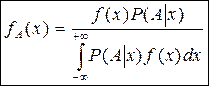
Пример:

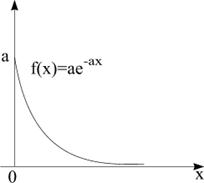
Плотность распределения с.в. Х – f(x)=ae^-ax (а ³ 0) - показательное распределение.

1) Построить кривую распределения

2) Найти и построить ф. Р. с. в. Х

3) Найти вероятность того, что с.в. Х примет значение, лежащее между

1 и 2

Решение:

1) Кривая распределения с.в. Х показана на рисунке.

2) По формуле для ф.р.:

При х< 0 f(x)=0 è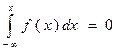

При х>0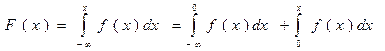

Þ функция распределения:

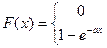
	при х<0
при х>0

График функции:

3) Вероятность попадания с. в. Х на (1, 2).

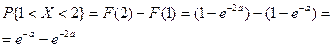
Глава 4 Числовые характеристики случайных величин.

Дата добавления: 2014-01-14