Модели в виде сигнальных графов

А б

Рис. 2.25. Представление звена системы:

а – структурное, б – функциональное

В частном случае оператора тождественного преобразования звено выступает как сумматор.

С точки зрения теории графов структурная схема является ориентированным графом 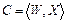, определяемым парой множеств: множеством вершин 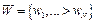и множеством дуг 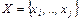, связывающих пары вершин. Вершины соответствуют звеньям, а дуги – связям. Вершина – это звено общего вида, суммирующее переменные всех входящих дуг. Дуга – компонент, задающий причинно-следственную связь между звеньями. В итоге структурная схема представляется структурным графом (С -графом), в котором отсутствуют звенья суммирования (рис. 2.24).

Теоретико-множественное описание систем дает естественный способ ввода и редактирования систем управления как последовательного раскрытия их по рангам неопределенности. Моделью нулевого структурного ранга системы M_s(0) является все множество звеньев. Для графа,

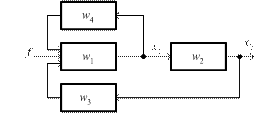
Рис 2.26. Структурный граф системы

приведенного на рис. 2.26, это множество перечисляется так:

W = { w ₁, w ₂, w ₃, w ₄}.

При однотипных звеньях можно ограничиться заданием мощности множества: │ W │ = 4.

Дополнение модели M_s(0) множеством связей

X = {(1,3), (1,4), (2,1), (3,2), (4,1)},

где цифры означают номера звеньев, даёт модель M_s(1) первого структурного ранга, т.е. модель топологии системы.

Дальнейшее раскрытие неопределенности состоит в задании операторов вершин, т.е. передаточных функций звеньев, определяемых отношениями полиномов

.

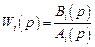Задание их структур сводится к указанию степеней n_i и m_i полиномов A_i и B_i, в результате образуется модель системы M_s(2) второго, т.е. структурного ранга. Если для рассматриваемого примера передаточные функции звеньев есть:

, , , ,

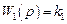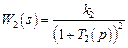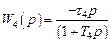то информацию о структурах операторов можно закодировать массивами степеней полиномов числителей и знаменателей передаточных функций: {0,0,0,1} и {0,2,0,1}.

Результат конкретизации значений всех коэффициентов полиномов – полностью определенная модель M_s(3) третьего, параметрического, ранга. В результате получаем описание автономной системы (т.е. собственно системы, вне связи со средой).

Для описания связей системы со средой необходимо указать звено, на которое подается входное воздействие, а также звено, выход которого является выходом системы.

Общие сведения о сигнальных графах. Для сложных систем процедура упрощения их структурных схем является весьма трудоемкой. Для таких систем Мейсоном был разработан альтернативный метод представления структуры системы сигнальным графом, позволяющий без каких-либо преобразований этого графа, с помощью специальной формулы, установить связи между переменными системы.В этом случае модель системы представляет собой бинарное отношение W на множестве переменных :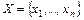

.

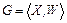Элементам отношения 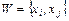ставятся в соответствие операторы преобразования переменных. На сигнальных графах переменным отвечают вершины, где суммируются сигналы входящих дуг, а элементам отношения – дуги. Компонент структурной схемы, изображенный на рис. 2.27

Рис. 2.27. Компонент структурной схемы

представляется сигнальным графом, представленным на рис. 2.28.

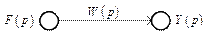
Рис. 2. 28. Сигнальный граф компонента структурной схемы,

приведенного на рис. 2.27

Преобразование переменных определяется наименованиями ветвей, стрелки определяют направление преобразования. Сумма всех сигналов, входящих в узел, образует соответствующую ему переменную. Ветвь (или последовательность ветвей), проведенная между двумя узлами, называется путем между ними. Замкнутый путь, начинающийся и заканчивающийся в одном и том же узле, причем в пути ни один узел не встречается дважды, называется контуром. Если два контура не имеют общего узла, то они называются непересекающимися.

Сигнальный граф, описывающий систему уравнений:

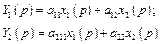(2.39)

приведен на рис. 2.29.

Рис.2.29. Сигнальный граф системы уравнений (2.39)

Отсюда следует, что сигнальный граф – это наглядный способ записи систем алгебраических уравнений, показывающий связь между переменными. А поскольку преобразование Лапласа преобразует дифференциальное уравнение в алгебраическое, то целесообразность применения сигнальных графов для исследования систем управления становится очевидной.

Рассмотрим систему алгебраических уравнений

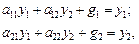(2.40)

где 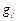– входные, а 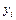– выходные переменные.

Соответствующий ей сигнальный граф показан на рис. 2.30.

Запишем приведенную систему уравнений в несколько ином виде:

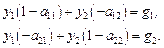
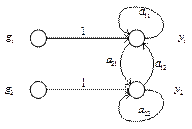
Рис. 2.30. Сигнальный граф системы уравнений (2.40)

Отсюда можно получить матрицы состояния

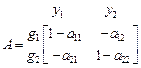
и управления

.

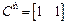Теперь выражения для определения выходных переменных в соответствии с правилом Крамера можно получить следующие соотношения:

,

,

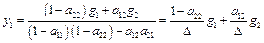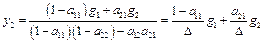где

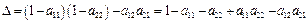
есть определитель матрицы состояния, составленный из коэффициентов при неизвестных, а числители выражений − определители, полученные из матрицы состояния заменой столбцов, соответствующих y ₁ и y ₂ столбцом свободных членов.

Из сравнения процессов получения выражений для переменных из матрицы состояния и из приведенного выше графа видно, что определитель графа равен единице за вычетом коэффициентов передачи отдельных контуров (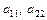и 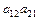) плюс произведение коэффициентов передачи двух не касающихся контуров (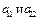) (контуры 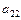и 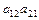– касающиеся, как и контуры 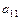и ).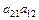

В решении для 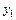по отношению к входу 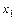числитель равен единице, умноженной на 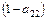, т.е. значению определителя не касающегося пути от 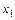к 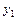. В решении для 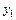по отношению к входу 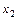числитель равен 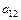, так как этот путь касается всех контуров. Числитель выражения для 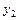симметричен числителю для .

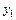Таким образом, между алгебраическим, матричным и графовым представлениями дифференциальных уравнений существует однозначная зависимость.

Формула Мейсона. В общем случае линейная зависимость 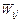независимой (входной) переменной 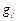и зависимой переменной 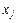определяется по формуле Мейсона

,

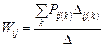где 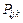– коэффициент передачи k -го пути от узла i к узлу j, 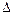– определитель графа, 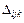– минор этого пути, равный определителю всех касающихся друг друга контуров при удалении k -го пути, а суммирование ведется по всем возможным путям от узла i к узлу j.

Определитель 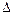находится как

,

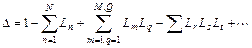где 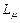– коэффициент передачи µ- го контура. Другими словами, 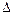определяется так:

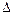= 1 – [ сумма коэффициентов передачи отдельных контуров ] + [ сумма произведений всех возможных комбинаций из двух непересекающихся (не касающихся) контуров ] –[ сумма произведений всех возможных комбинаций из трех непересекающихся контуров ] +… + …и т.д.

В несколько упрощенном виде формула Мейсона часто используется для определения передаточной функции.Она дает возможность определить передаточную функцию пути от вершины A (вход) до вершины B (выход) графа как

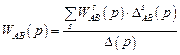, (2.41)

где 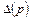– определитель графа, определяемый как

,

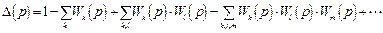где 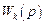– передаточные функции контуров (замкнутых путей) графа,

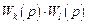– произведения не касающихся друг друга (не имеющих общих вершин) пар контуров,

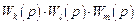– произведения передаточных функций, попарно некасающихся троек контуров и т.д.,

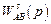– передаточная функция разомкнутого s -го пути из вершины A в вершину B,

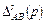– минор s-го пути (определитель подграфа, полученного удалением из графа s -го пути).

Пример 2.16. Найти передаточную функцию между вершинами f и y сигнального графа, приведенного на рис.2.31.

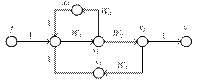
Рис. 2. 31. Сигнальный граф

Решение. Граф имеет два касающихся контура с передаточными функциями

;

.

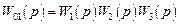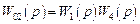Определитель графа равен

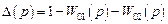
(не касающиеся контуры отсутствуют, поэтому членов-произведений нет).

Между входом f и выходом y имеется лишь один прямой путь с передаточной функцией

.

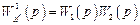После удаления этого пути не остается ни одного контура, поэтому минор этого пути равен

.

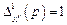Таким образом, передаточная функция графа между вершинами f и y определится как

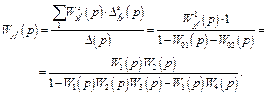
Знаменатель последнего выражения есть характеристический полином системы.

■

Разновидности сигнальных графов. Модель системы в виде графа с переменными состояния в узлах легко получить по передаточной функции. Но поскольку возможны несколько комбинаций переменных состояния, то можно построить несколько сигнальных графов. Рассмотрим общую методику построения сигнальных графов по передаточной функции на примере системы четвертого порядка с передаточной функцией общего вида

.

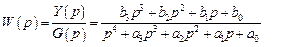Умножим числитель и знаменатель передаточной функции на 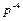(в общем случае – на

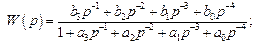(2.42)

Слагаемые в числителе – коэффициенты передачи прямых путей, а переменные состояния − выходы интеграторов в формуле Мейсона. Прямые пути касаются всех контуров, поэтому сигнальный граф системы будет иметь вид, показанный на рис. 2.32.

Для получения системы дифференциальных уравнений первого порядка, соответствующей выражению (2.40), введем в граф дополнительные узлы, предшествующие каждому интегратору. При

Рис. 2.32. Граф состояния для (2.42) системы

в форме фазовой переменной

этом каждый узел будет соответствовать производной входной переменной интегратора. В результате граф приобретает вид, показанный на рис. 2.33.

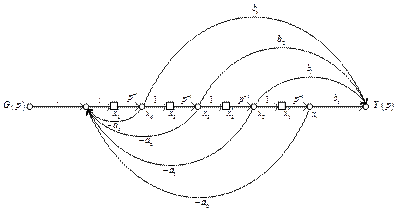
Рис. 2.33. Сигнальный граф с дополнительными узлами

Это представление графа системы называется представлением в форме с фазовой переменной.

По этому графу можно записать следующую систему дифференциальных уравнений первого порядка:

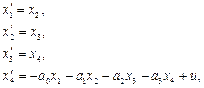
где 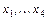– фазовые переменные. Уравнение наблюдения имеет вид

.

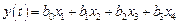Эти же уравнения в матричной форме выглядят следующим образом:

,

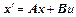или

,

.

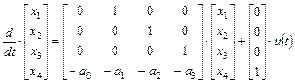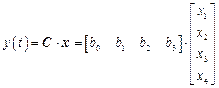Другая конфигурация сигнального графа, соответствующая той же передаточной функции (2.42), приведена на рис. 2.34. Она называется формой представления с многомерным входом.

Отличие этой модели состоит в том, что в ней коэффициенты передачи прямых путей образуются заведением сигнала 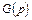на вход каждого из интеграторов. Выходной сигнал здесь равен переменной состояния 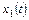. Коэффициенты передачи прямых путей здесь равны 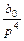,,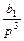 , 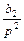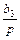и все эти пути касаются контуров, поэтому передаточная функция действительно соответствует выражению (2.40).

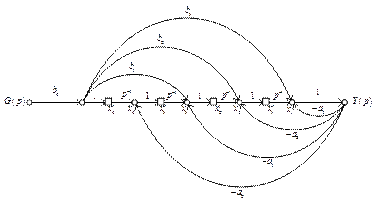
Рис. 2.34. Альтернативный граф,

соответствующий передаточной функции (2.42)

По графу (рис.2.34) можно записать следующую систему дифференциальных уравнений первого порядка

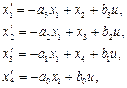
или в матричной форме

.

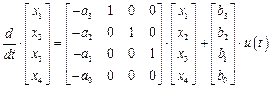Графы в форме с многомерным входом и с фазовой переменной

соответствуют одной и той же передаточной функции, однако их переменные состояния не равны, поскольку структура графов различна.

Пример 2.17. Построить графы со структурами в формах с фазовой переменной и с многомерным входом для системы, показанной на рис. 2.35.

Рис. 2.35. Пример задания системы передаточной функцией

Решение. Передаточная функция замкнутой системы есть

.

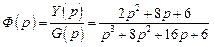Умножая числитель и знаменатель на 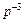, получим

.

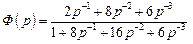Соответствующая последнему выражению модель (граф) в форме с фазовой переменной приведена на рис. 2.36.

Рис. 2.36. Граф системы со структурой в форме с фазовой переменной

Уравнение состояния системы из графа имеет вид

,

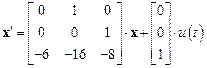а уравнение наблюдения (выхода) есть

.

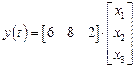Граф системы в форме с многомерным входом приведен на рис.2.37. Для него уравнение состояния есть

,

а уравнение наблюдения

.

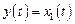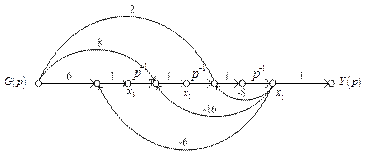
Рис. 2.37. Граф системы в форме с многомерным входом

■

Оба сигнальных графа, соответствующих передаточной функции 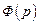, строятся просто, без разложения полиномов числителя и знаменателя на элементарные множители. Это позволяет избежать трудоемких вычислений, а по структуре графа легко записать уравнение состояния. Поскольку система имеет третий порядок, то для ее моделирования необходимы три интегратора. Отметим, что хотя переменные в обеих моделях не идентичны друг другу, то комбинации переменных обеих моделей связаны линейным преобразованием вида .

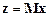Дата добавления: 2014-01-15