Решение систем линейных уравнений

В матричной записи общая задача решения систем линейных уравнений имеет следующий вид: заданы две матрицы A и B, существует ли единственная матрица X такая, что AX = B или XA = B? Например, в скалярном случае, имеет ли уравнение

7 х = 21

единственное решение? Ответ положительный, единственное решение x = 3. Решение легко найдено в результате деления,

х = 21/7

Более сложный и менее точный путь решения этого уравнения – вычисление обратной величины от 7, 7^-1 = 0.142857..., и, затем, умножение 7^-1 на 21. Программное обеспечение MATLAB экономно решает системы линейных без вычисления обратной матрицы.

В MATLAB используется не общепринятое математическое обозначение для описания решения общей системы совместимых линейных уравнений. Два разделительных символа, слэш (slash), /, и обратный слэш (backslash), \, соответствуют двум функциям MATLAB mldivide и mrdivide. Функции mldivide и mrdivide используются в двух случаях, в зависимости от того слева или справа от матрицы коэффициентов появляется неизвестная матрица:

X = B/A определяет решение матричного уравнения XA = B (для обеспечения соответствия размерностей, число столбцов матриц А и В должно быть одинаковым, при этом решение X имеет то же число строк, что и В, и число столбцов равное числу строк в А).

X = A\B определяет решение матричного уравнения AX = B (число строк

матриц А и В должно быть одинаковым, решение X имеет то же число столбцов, что и В, и число строк равное числу столбцов в А).

Так как на практике системы линейных уравнений вида AX = B встречаются на практике чаще, чем XA = B, соответственно чаще используется обратный слэш, \, чем прямой. В применении этих двух операторов может быть установлено соответствие:

(B/A)' = (A'\B')

Матрица коэффициентов не обязательно должна быть квадратной. Если А имеет размерность m×n, существует три случая

1) m = n – квадратная система, точное решение;

2) m > n – переопределенная система, решение по методу наименьших квдратов;

3) m < n – недоопределенная система, базовое m-компонентное решение.

Общее решение. Общее решение системы линейных уравнений AX = b описывает все возможные решения. Общее решение можно найтиследующим образом:

1. Решить соответствующую однородную систему AX = 0. Это можно сделать используя функцию null, ввести null(A). Функция null возвращает базис для пространства решений AX = 0. Любое решение является линейной комбинацией базисных векторов.

2. Найти частное решение неоднородной системы AX = b. Тогда можно записать любое решение AX = b как сумму частного решения AX = b, полученного на 2-м шаге, плюс линейная комбинация базисных векторов полученных на 1-м шаге.

Решение квадратных систем линейных уравнений.

Наиболее часто встречается ситуация квадратной матрицы коэффициентов A и вектора-столбца в правой части уравнения b.

Несингулярная матрица коэффициентов. Если матрица A несингулярная, решение, x = A\b, имеет тот же размер, что и b. Напимер:

A = pascal(3);

u = [3; 1; 4];

x = A\u

x =

-12

Если А и В квадратные матрицы одинакового размера, тогда X = A\B имеет тот же размер:

B = magic(3);

X = A\B

X =

19 -3 -1

-17 4 13

6 0 -6

Сингулярная матрица коэффициентов. Матрица A сингулярная, если она не имеет линейно независимых столбцов. Если A сингулярная, то решение AX = B либо не существует, либо оно не единственно. Оператор обратный слэш, A\B, выводит предупреждение если A близка к сингулярной или если A сингулярная.

Если A сингулярная и AX = b имеет решение, Вы можете найти частное неединственное решение, напечатав

P = pinv(A)*b

где P – псевдообратная матрица от A. Если A не имеет точного решения, pinv(A)

возвратит решение, полученное по методу наименьших квадратов. Например,

A = [ 1 3 7; -1 4 4; 1 10 18]

является сингулярной, что можно установить напечатав,

det(A)

ans =

Для

b =[5; 2; 12]

уравнение AX = b имеет точное решение, которое получим используя:

pinv(A)*b

ans =

0.3850

-0.1103

0.7066

Проверим решение,

A*pinv(A)*b

ans =

5.0000

2.0000

12.0000

Если

b = [3; 6; 0]

AX = b не имеет точного решения. В этом случае, pinv(A)*b возвратит решение, полученное по методу наименьших квадратов,

pinv(A)*b

ans =

-1.0892

1.2512

-0.5235

В результате проверки первоначальный вектор b не получается,

A*pinv(A)*b

ans =

-1.0000

4.0000

2.0000

Определить имеет ли система AX = b единственное решение можно в результате нахождения дополнения матрицы [A b]. Для нашего примера, введем

rref([A b])

ans =

1.0000 0 2.2857 0

0 1.0000 1.5714 0

0 0 0 1.0000

Так, как нижняя строка состоит из всех нулей исключая последнюю позицию, уравнение не имеет решения. pinv(A) возвращает решение, полученное по методу наименьших квадратов.

Решение переопределенных систем линейных уравнений.

Переопределенные системы совместимых линейных уравнений часто встречаются при подборе разного типа кривых по экспериментальным данным. Прведем пример, величина y измерена в различные моменты времени, t,

t y

0.0 0.82

0.3 0.72

0.8 0.63

1.1 0.60

1.6 0.55

2.3 0.50

Введем данные в MATLAB:

t = [0.3.8 1.1 1.6 2.3]';

y = [.82.72.63.60.55.50]';

Попробуем описать эти данные затухающей экспоненциальной функцией,

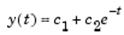
Из этого уравнения видно, что вектор y можно аппроксимировать линейной комбинацией двух векторов, одиного вектора, составленного из единиц, и другого из компонент e ^{– t}. Неизвестные коэффициенты, c ₁ и c ₂, могут быть вычислены по методу наименьших квадратов, который минимизирует сумму квадратов отклонений исходных данных от модели. Имеется шесть уравнений с двумя неизвестными, которые представляют матрицу размерности 6×2:

E = [ones(size(t)) exp(-t)]

E =

1.0000 1.0000

1.0000 0.7408

1.0000 0.4493

1.0000 0.3329

1.0000 0.2019

1.0000 0.1003

Используем оператор обратный слэш для получения решения по методу наименьших квадратов:

c = E\y

c =

0.4760

0.3413

Другими словами, подбор по методу наименьших квадратов дает:

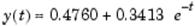
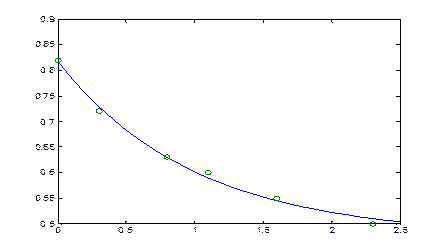
Оценим по графику соответствие модели исходным данным, задав постоянное приращение времени t: data:

T = (0:0.1:2.5)';

Y = [ones(size(T)) exp(-T)]*c;

plot(T,Y,'-',t,y,'o')

Решение недоопределенных систем линейных уравнений.

Прямоугольная матрица A n×m (n < m) имеет неполный ранг (r < n) если она не имеет линейно независимых столбцов. Если A имеет неполный ранг то решение уравнения AX = B по методу наименьших квадратов не является единственным. Оператор обратный слэш, A\B, выдает предупреждение, если матрица A имеет неполный ранг. Частное решение недоопределенные систем линейных уравнений может быть получено следующим способом. Например, формируем недоопределенную систему линейных уравнений:

R = fix(10*rand(2,4))

R =

9 6 8 4

2 4 7 0

b = fix(10*rand(2,1))

b =

устанавливаем дробно-рациональный числовой формат

format rat

получаем вектор-столбец частного решения системы

p = R\b

p =

24/47

20/47

Полное решение недоопределенной системы получается добавлением вектора из нулевого пространства, которое может быть найдено в результате применения функции null с заданием опции дробно-рационального базиса:

Z = null(R,'r')

Z =

5/12 -2/3

-47/24 1/3

1 0

0 1

Подтверждение того, что R*Z есть нуль

R*Z

ans =

0 0

0 0

тогда вектор x, где

x = p + Z*q

для произвольного вектора q удовлетворяет R*x = b, проверим:

q=[1 2];

x=p+Z*q'

x =

-0.4060

-1.2917

1.4255

2.0000

R*x

ans =

4.1.3. Обращение матрицы и вычисление ее определителя.

Если матрица A является квадратной и несингулярной, уравнения AX = I и XA = I имеют одинаковое решение. Это решение называется обращением (инверсией) матрицы A, обозначается A ^-1, и вычисляется функцией inv.

Понятие определителя (детерминанта) матрицы A используется в теории матриц и некоторых типах вычислений. Детерминант квадратной матрицы вычисляет функция det:

A = pascal(3)

A =

1 1 1

1 2 3

1 3 6

d = det(A)

X = inv(A)

d =

X =

3 -3 1

-3 5 -2

1 -2 1

Если A квадратная и несингулярная, тогда X = inv(A)*B теоретически является тем же, что X = A\B и Y = B*inv(A) то же, что Y = B/A. Вычисления с использованием оператора обратного слэша предпочтительнее, т.к. требуют меньше времени, меньше памяти и являются более точными.

Псевдоинверсии. Прямоугольные матрицы не имеют обратных матриц или определетилей. По крайней мере одно из уравнений AX = I и XA = I не имет решения. Частичная замена для обратной матрицы обеспечивается псевдоинверсией Мура-Пенросе, которая вычисляется функцией pinv:

format short

C = fix(10*gallery('uniformdata',[3 2],0));

X = pinv(C)

X =

0.1159 -0.0729 0.0171

-0.0534 0.1152 0.0418

Матрица

Q = X*C

Q =

1.0000 0.0000

0.0000 1.0000

единичная 2×2, но матрица

P = C*X

P =

0.8293 -0.1958 0.3213

-0.1958 0.7754 0.3685

0.3213 0.3685 0.3952

не является единичной 3×3 identity. Однако, P действует как единичная на часть пространства в смысле того, что P является симметричной, P*C равно C, и X*P равно X.

Решение недоопределенных систем линейных уравнений.

Если матрица A имеет размерность m×n при m > n и рангом n, следующие три записи

x = A\b

x = pinv(A)*b

x = inv(A'*A)*A'*b

дают одно и то же численное решение x по методу наименьших квадратов. Однако, если ранг матрицы A меньше n, решение x по методу наименьших квадратов не будет единственным. Имеется много векторов x, которые минимизируют

norm(A*x – b)

Решение x = A\b является базисным; оно имеет не больше чем r ненулевых компонент, где r – ранг A. Решение x =pinv(A)*b является решением с минимальной нормой, т.к. оно минимризирует norm(x). Попытка использовать для вычисления решения x = inv(A'*A)*A'*b будет неудачной, т.к. A'*A является сингулярной.

Примеры, иллюстрирующие различные решения:

A = [ 1 2 3

4 5 6

7 8 9

10 11 12]

эта матрица имеет неполный ранг, т.к. 2-й столбец есть среднее 1-го и 3-го. Если

b = A(:,2)

2-й столбец, то очевидым решением A*x = b есть x = [0 1 0]'. Оператор обратного слэша дает,

x = A\b

Warning: Rank deficient, rank = 2 (Предупреждение: неполный ранг, ранг = 2).

x =

0.5000

0.5000

Это решение имеет два ненулевых компонента. Применение псевдоинверсии дает

y = pinv(A)*b

y =

0.3333

0.3333

0.3333

Здесь нет предупреждения о неполном ранге. Но norm(y) = 0.5774 меньше norm(x) = 0.7071. Окончательно,

z = inv(A'*A)*A'*b

получаем предупреждение:

Warning: Matrix is close to singular or badly scaled (Матрица близка к сингулярной или плохо обусловлена)

Results may be inaccurate (Результат может быть некорректным). RCOND = 9.868649e-018.

z =

-0.8594

1.3438

-0.6875

4.1.4. Матричная степень и экспонента.

Положительные целые степени. ЕслиA квадратная матрица и p положительное целое, A^p умножает A саму на себя p – 1 раз. Например:

A = [1 1 1;1 2 3;1 3 6]

X = A^2

X =

3 6 10

6 14 25

10 25 46

Обращение (инверсия) и дробные степени. Если А квадратная и несингулярная, A^(–p) умножает обратную матрицу inv(A) саму на себя p – 1 раз:

Y = A^(-3)

Y =

145.0000 -207.0000 81.0000

-207.0000 298.0000 -117.0000

81.0000 -117.0000 46.0000

Дробные степени, как A^(2/3), также допустимы; результат зависит от распределения собственных значений матрицы.

По-элементные степени. Результатом действия оператора.^ являются по-элементные степени. Например:

A.^3

ans =

1 1 1

1 8 27

1 27 216

Экспоненты. Функция sqrtm(A) вычисляет A^(1/2) в соответствии с более точным алгоритмом. m в sqrtm отличает эту функцию от sqrt(A), которая как A.^(1/2), делает вычисления по-элементно. Cистема линейных, обыкновенных дифференциальных уравнений с постоянными коэффициентами может быть записана в виде:

dx / dt = Ax

где x = x (t) – вектор функций от t и A – матрица, не зависящая от t. Решенеи может быть представлено в виде матричной экспоненты

x (t) = e^At x (0)

Функция

expm(A)

вычисляет матричную экспоненту. Пример с использованием матрицы коэффициентов 3×3

A = [0 -6 -1

6 2 -16

-5 20 -10]

и начальным условием, x (0)

x0 = [1; 1; 1]

Матричная экспонента использована для вычисления решения, x (t), дифференциального уравнения в 101 точке на интервале 0 ≤ t ≤ 1. Вычислительный код решения задачи:

X = [];

for t = 0: 0.01: 1

X = [X expm(t*A)*x0];

end

plot3(X(1,:),X(2,:),X(3,:),'-o') % Рисует график решения в 3-х мерном

фазовом пространстве

Cобственные значения и собственные вектора квадратной матрицы A являются, соответственно, скаляр λ и ненулевой вектор v, которые удовлетворяют условию

Аv = λv

С собственными значениями на диагонали диагональной матрицы Λ и с собственными векторами, формирующими столбцы матрицы V, имеем

АV = VΛ

Если V несингулярная, получим разложенеи по собственным значениям

АV = VΛV ^–1

Для матрицы из предыдущего примера:

A = [0 -6 -1

6 2 -16

-5 20 -10]

Результатом задания

lambda = eig(A)

является вектор-столбец, содержащий собственные значения. Для этой матрицы собственные значения являются комплексными числами:

lambda =

-3.0710

-2.4645+17.6008i

-2.4645 -17.6008i

Действительные части собственных значений являются отрицательными, так, что при увеличении t e^λt стремится к нулю. Ненулевые мнимые части двух собственных значений, ± ω, вносят колебательную составляющую, sin(ωt), в решение дифференциального уравнения. С двумя выходными аргументами, функция eig вычисляет собственные вектора и хранит собственные значения в диагональной матрице:

[V, D] = eig(A)

V =

-0.8326 0.2003 - 0.1394i 0.2003 + 0.1394i

-0.3553 -0.2110 - 0.6447i -0.2110 + 0.6447i

-0.4248 -0.6930 -0.6930

D =

-3.0710 0 0

0 -2.4645+17.6008i 0

0 0 -2.4645-17.6008i

Все три собственные вектора нормализованы, их Евклидова длина равна единице.

Сингулярные величины. Сингулярные значения и соответствующие сингулярные вектора прямоугольной матрицы A есть, соответственно, скаляр σ и пара векторов u и v, которые удовлетворяют условию

Av = σu

A^Тu = σv

С сингулярными значениями на диагонали диагональной матрицы Σ и соответствующими сингулярными векторами, формирующими столбцы двух ортогональных матриц U и V, имеем

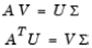
Т.к. U и V ортогональны, возможно разложение по сингулярным значениям

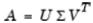
Полное разложение по сингулярным величинам матрицы m×n включает матрицы m×m U, n×n V и m×n Σ. Матрицы U, и V обе квадратные, а Σ имеет ту же размарность, что и A. Разложение по сингулярным величинам является подходящим инструментом для анализа матрицы, когда она представляет отображение векторного пространства на себя, как это имеет место в случае обыкновенных дифференциальных уравнений. Разложение по сингулярным величинам применимо при анализе отображения векторного пространства на другое векторное пространство, которое имеет другую размерность чем первое. Многие системы совместимых линейных уравнених соответстуют второй категории.

Для квадратной, симметричной и положительно определенной матрицы A, разложения по собственным и сингулярным величинам являются одинаковыми. При увеличении несимметрии и неположительной определенности матрицы A, разница между двумя разложениями увеличивается. В частности, разложение по сингулярным величинам вещественной матрицы является вещественным, но разложение по собственным величинам вещественной несимметричной матрицы может давать комплексные числа.

Дата добавления: 2014-01-11